
Liegt eine reinquadratische Gleichung vor, so kann man diese natürlich auch über die Anwendung der p-q-Formel lösen! Das geht natürlich – das ist aber alles andere als logisch sinnvoll! In Mathe geht es ja auch beim Aufgabenlösen um den möglichst unkomplizertesten und damit auch schnellesten Weg. Neben einer Zeitersparnis ist dieser Weg auch immer mit einem Fehlerverringerungsrisiko verbunden. Ein Musterbeispiel stellt hierfür eine reinquadratische Gleichung dar. Da diese keinen Mittelterm vorweist, kann diese im Nu durch ein Wurzelziehen gelöst werden. Mit der p-q-Formel geht das, wie gesagt, auch, das dauert aber viel, viel länger. Auch besteht hierbei die Gefahr, dass man einen Leichtsinnsfehler macht – und wirklich unnötige und somit wirklich ärgerliche Punkte verliert. Das spiegelt sich ja wiederum in der Mathe-Note wider!
Aufgaben zu dem Mathematik-Stoffgebiet quadratische Gleichungen
1. Mathe Nachhilfe-Aufgabe: Löse die reinquadratischen Gleichungen möglich sinnvoll, die anderen quadratischen Gleichungen ebenso.
a) 0,25a² = 25
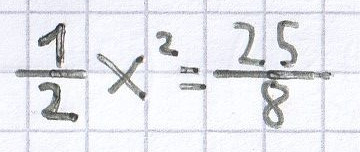
4x² + 1 = 0
b)
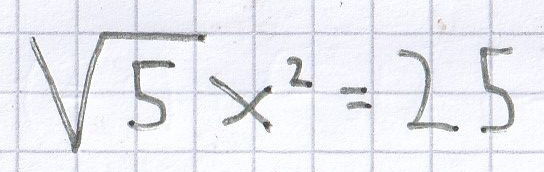
0,24y² – 6 = 0

c) (x – 4)² + (x + 4)² = 34;
–3(x + 8) = (x – 8) · (x + 5)
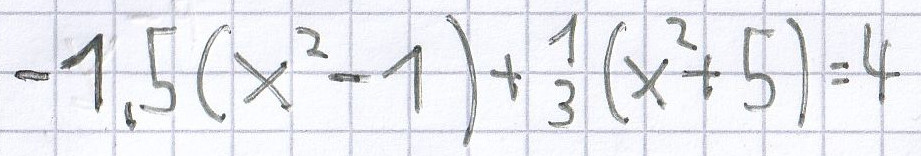
2. Mathe-Nachhilfe-Aufgabe: Bestimme bei folgenden quadratischen Gleichungen zunächst jeweils die Lösungsmenge und überprüfe anschließend das Ergebnis mittels Probe.
a) (a – 5)² = –25
b) (x – 2)² = 16
c) (x + 1,2)² = 0,49
d) (x – 0,6)² = 20,25
Lösungen zum Mathematik-Stoffgebiet Quadratische Gleichungen
1. Mathe-Nachhilfe-Aufgabe: Löse die reinquadratischen Gleichungen so sinnvoll wie möglich, die anderen Gleichungen ebenso.
a) 0,25a² = 25 | : 0,25
Hier muss man wiederum zuerst die „nackte“ Zahl vor der Potenz eliminieren. Darauf kann man die Wurzel ziehen und die Lösung der quadratischen Gleichung ermitteln.
a² = 100 | √
a = ± 10
L = {–10; 10}
a)

Hier gilt wieder das Gleiche, dass man zuerst den Faktor vor der Potenz entfernen muss. Darauf kann man nach dem Ziehen der Wurzel sofort die Lösung der quadratischen Gleichung bestimmen.
x² = 6,25 | √
x = ± 2,5
L = {–2,5 ; 2,5 }
a) 4x² + 1 = 0 | – 1
Hier muss zuerst die „nackte“ Zahl auf die andere Seite der Gleichung gebracht werden. Darauf entfernt man den Faktor vor der Potenz und zieht die Wurzel. Dann erhält man die Lösung der quadratischen Gleichung.
4x² = –1 | : 4
x² = –0,25 | √
x = nicht definiert/n. d.
L = x = { } bzw. Ø
b)
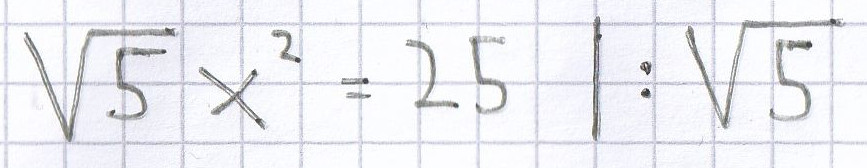
Hier gilt erneut, dass man zuerst den Faktor vor der Potenz entfernen muss. Darauf kann man nach dem Wurzelziehen die Lösung der quadratischen Gleichung ermitteln.

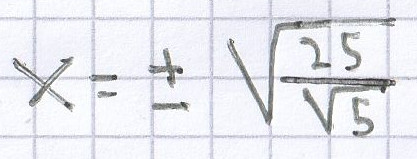
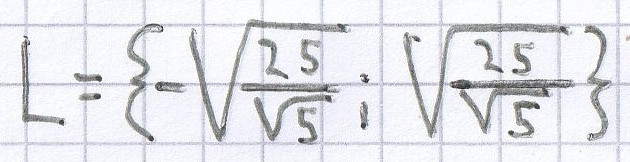
b) 0,24y² – 6 = 0 | + 6
Bei dieser quadratischen Gleichung muss man wiederum zuerst die „nackte“ Zahl auf die andere Seite der Gleichung bringen. Anschließend eliminiert man den Faktor vor der Potenz. Nach dem Wurzelziehen kann man die Lösung der Gleichung bestimmen.
y² – 6 = 0 | + 6
y² = 6 | √
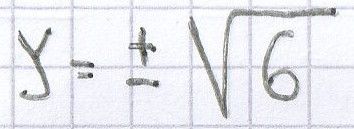
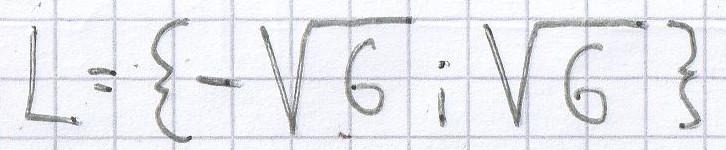
b)
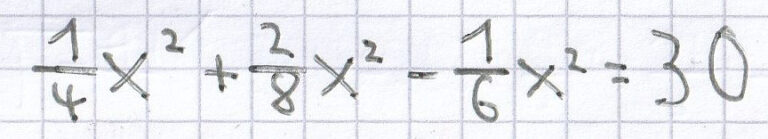
Hier muss man zuerst alle gleichen Einzelterme zusammenfassen. Darauf entfernt man die „nackte“ Zahl vor der Potenz. Nach dem Wurzelziehen kann man die Lösung der quadratischen Gleichung ermitteln.
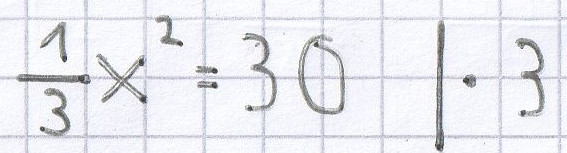
x² = 90 | √

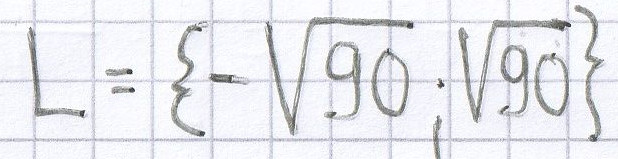
c) (x – 4)² + (x + 4)² = 34
Hier muss man erst die beiden binomischen Formeln auflösen. Darauf die gleichen Einzelterme zusammenfassen. Danach mittels Äuqivalenzumformung die Gleichung weiter vereinfachen und dann die „nackte“ Zahl vor der Potenz eliminieren. Nach dem Ziehen der Wurzel erhält man schließlich die Lösung der quadratischen Gleichung.
(x)² – 2 · x · 4 + (4)² + (x)² + 2 · x · 4 + (4)² = 34
x² – 8x + 16 + x² + 8x + 16 = 34
2x² + 32 = 34 | – 32
2x² = 2 | : 2
x² = 1 | √

x = ± 1
L = {–1; 1}
c) –3(x + 8) = (x – 8) (x + 5)
Zunächst muss man hier die Klammern mittels des Distributivgesetzes/Verteilungsgesetzes korrekt auflösen und darauf die gleichen Einzelterme zusammenfassen, dann mittels Äquivalenzumformungen die Gleichung weiter vereinfachen. Nach dem Wurzelziehen erhält man die Lösung der quadratischen Gleichung.
(–3) · x + (–3) · 8 = x · x + x · 5 + (–8) · x + (–8) · 5
–3x – 24 = x² + 5x – 8x – 40
–3x – 24 = x² – 3x – 40 | + 3x
– 24 = x² – 40 | + 40
16 = x² | √
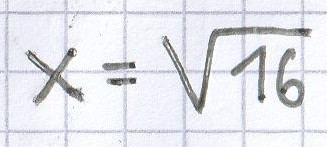
x = ± 4
L = {–4; 4}
c)
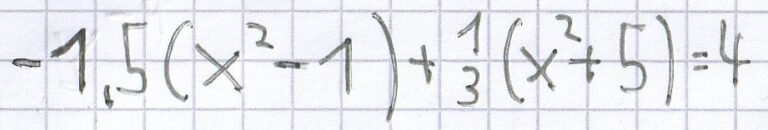
Hier muss man ebenso zunächst die Klammern korrekt auflösen, indem man das Distributivgesetz/Verteilungsgesetz anwendet. Nach dem Zusammenfassen gleicher Einzelterme muss man die Gleichung mittels Äquivalenzumformungen weiter vereinfachen. Die Lösung der quadratischen Gleichung zeigt sich nach dem Wurzelziehen.
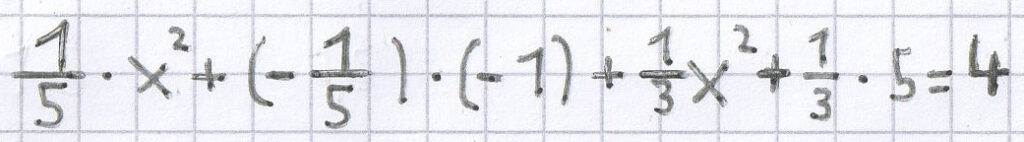

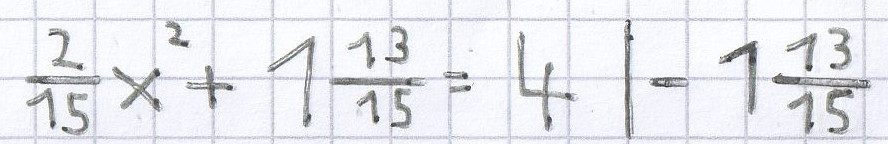
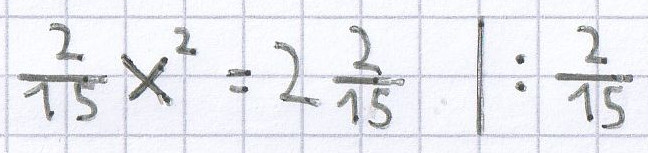
x² = 16 | √

x = ± 4
L = {–4; 4}
2. Mathematik-Nachhilfe-Aufgabe: Löse die quadratische Gleichung und bestätige anschließend das Ergebenis mittels Probe.
a) (a – 5)² = –25 | √

a = nicht definiert
L = { } bzw. Ø
Da hier eine negative Wurzel vorliegt, gibt es keine Lösung für die quadratische Gleichung.
b) (x – 2)² = 16 | √
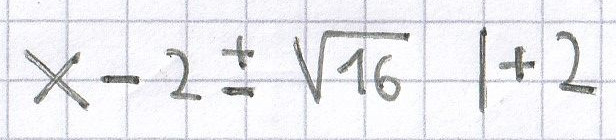
x = ± 4 + 2
x1 = –4 + 2 = –2; x2 = 4 + 2 = 6
L = {–2; 6}
Probe: (–2 – 2)² = 16
(–4)² = 16
16 = 16
(6 – 2)² = 16
(4)² = 16
16 = 16
Die Probe bestätigt, dass die Lösung der quadratischen Gleichung korrekt ist.
c) (x + 1,2)² = 0,49 | √
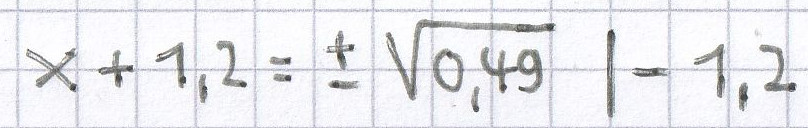
x = ± 0,7 – 1,2
x1 = –0,7 – 1,2 = –1,9; x2 = 0,7 – 1,2 = –0,5
L = {–1,9; –0,5}
Probe:
(–1,9 + 1,2)² = 0,49
(–0,7)² = 0,49
0,49 = 0,49
(–0,5 + 1,2)² = 0,49
(0,7)² = 0,49
0,49 = 0,49
Die Probe zeigt auf, dass die Lösung der quadratischen Gleichung korrekt ist.
d) (x – 0,6)² = 20,25 | √
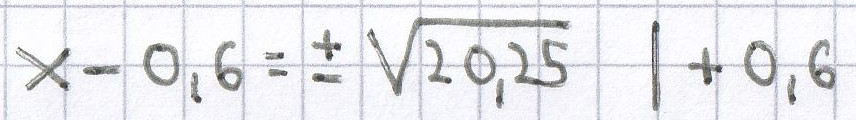
x = ± 4,5 + 0,6
x1 = –4,5 + 0,6 = –3,9; x2 = 4,5 + 0,6 = 5,1
L = {–3,9; 5,1}
Probe:
(–3,9 – 0,6)² = 20,25
(–4,5)² = 0,49
20,25 = 0,49
(5,1 – 0,6)² = 20,25
(4,5)² = 20,25
20,25 = 20,25
Auch hier legt die Probe offen, dass die Lösung der quadratischen Gleichung korrekt ist.