1. Bestandteile und Besonderheiten eines Logarithmus
Es sind folgende Gleichungen gegeben:
2x = 16
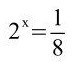
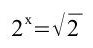
Der Exponent der Gleichungen ist hierbei jeweils gesucht, da dieser die Variable beinhaltet. Um die Lösung der Gleichung zu ermitteln, muss man einen Exponenten finden, durch den die jeweilige Gleichung wahr wird.
Bei der Gleichung 2x = 16 ist x = 4 die Lösung der Gleichung.
Denn: 24 = 16.
Bei der Gleichung
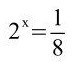
ist x = –3 die Lösung der Gleichung.
Denn:
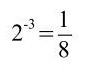
Bei der Gleichung
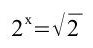
ist
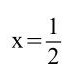
die Lösung der Gleichung.
Denn:
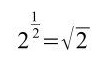
Durch das Anwenden der Potenzgesetze kann man den Exponenten einer derartigen Gleichung ermitteln. Über den Logarithmus geht das ebenso – und auch bei Exponenten, die nicht ganz so einfach zu ermitteln sind.
Definition
Es sind zwei positive Zahlen y und b (b ≠ 1) gegeben.
1. Unter dem Logarithmus von y zu Basis b bezeichnet man diejenige Zahl x, mit dem man b potenzieren muss, um y zu erhalten. Es gilt daher für die Zahl x Folgendes: bx = y.
Die Schreibweise hierfür ist: logb y.
Die Zahl y vor dem logb-Symbol nennt man Numerus.
Als Logarithmieren wird das Ermitteln des Logarithmus von y zur Basis b bezeichnet.
2. Liegt ein Logarithmus zur Basis 10 vor, so ist anstatt log10 die gängige Schreibweise lg (für den dekadischen Logarithmus).
Beispiele:
Ermittle log2 16 heißt: Bestimme den Exponenten x, so dass 2x = 16 ergibt.
Ermittle
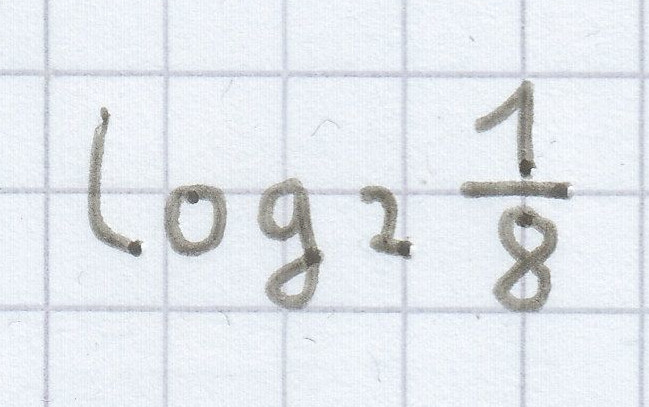
heißt: Bestimme den Exponenten x, so dass
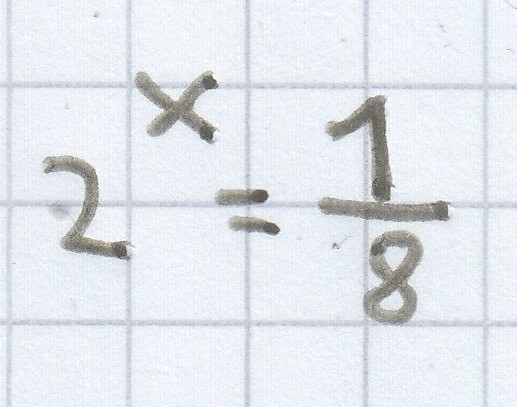
ergibt.
Ermittle
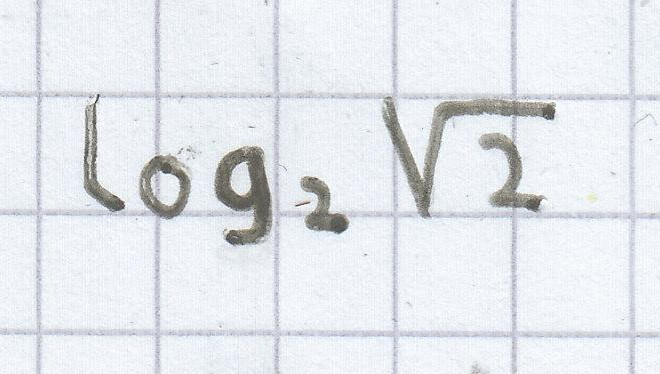
heißt: Bestimme den Exponenten x, so dass
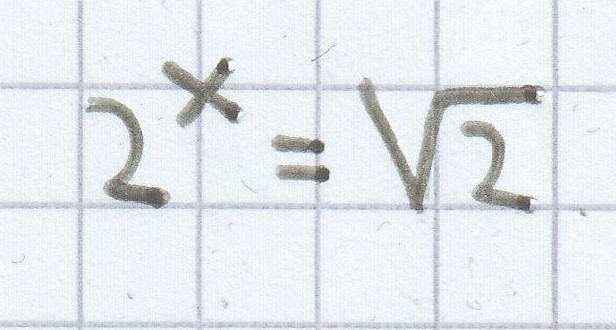
ergibt.
Die Wechselbeziehung zwischen Logarithmus und Potenz gibt man in der Mathematik folgendermaßen wieder:
logb y = x entspricht: bx = y Da ein Logarithmus sich immer auf eine Potenz zurückführen lässt, die die Basis bx vorweist, sind alle Logarithmuswerte stets positiv (da immer gilt: b > 0).
Beispiele:
log2 64 entspricht: 2x = 64. Daher ist x = 6.
log3 9 entspricht: 3x = 9. Daher ist x = 2.
log4 4 entspricht: 4x = 4. Daher ist x = 1.
lg 100 entspricht: 10x = 100. Daher ist x = 2.
Beachte: lg = log10
2. Logarithmieren und Potenzieren als Gegenrechenoperationen
Das Logarithmieren stellt die Gegenrechenoperation des Potenzierens dar. Bereits vom Addieren und dessen Gegenrechenoperation dem Subtrahieren sowie vom Multiplizieren und dessen Gegenrechenoperation dem Dividieren weiß man: Gegenrechenoperationen heben sich gegenseitig auf. Das ist auch beim Logarithmieren und Potenzieren der Fall.
2.1 Das Logarithmieren und das Potenzieren
Das Logarithmieren und das Potenzieren heben sich als Gegenrechenoperationen auf.
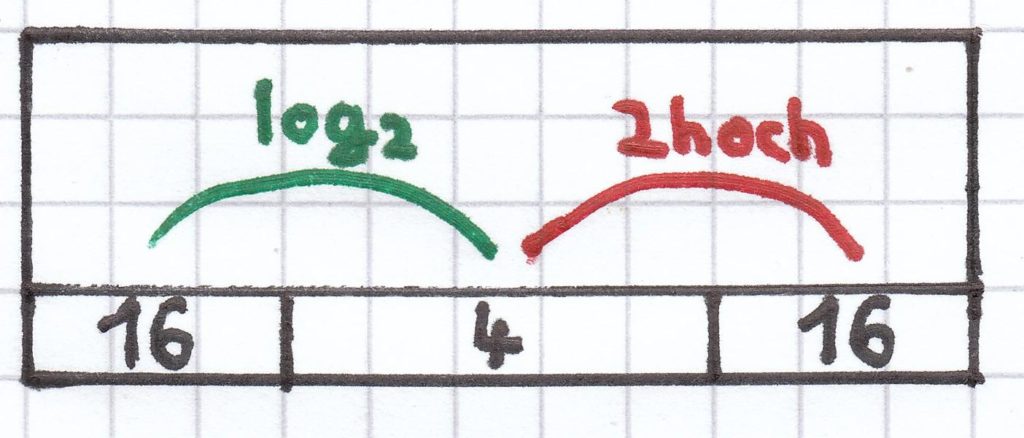
In Worten wiedergegeben: Der Logarithmus zur Basis 2 mit dem Numerus 16 ergibt 4 (Logarithmiere 16 von 4). Die Basis 2 mit dem Exponenten 4 ergibt 16 (Potenziere 2 hoch 4). Hieraus folgt: „log2 und 2 hoch“ heben sich als Rechenoperationen gegenseitig auf.
Das Potenzieren zur Basis b ist die Gegenrechenoperation des Logarithmierens zu Basis b.
Es gilt daher:

für alle x Є ℝ+
Beispiele:
log2 16 = 4 entspricht: 24 = 16
log2 8 = 3 entspricht: 23 = 8
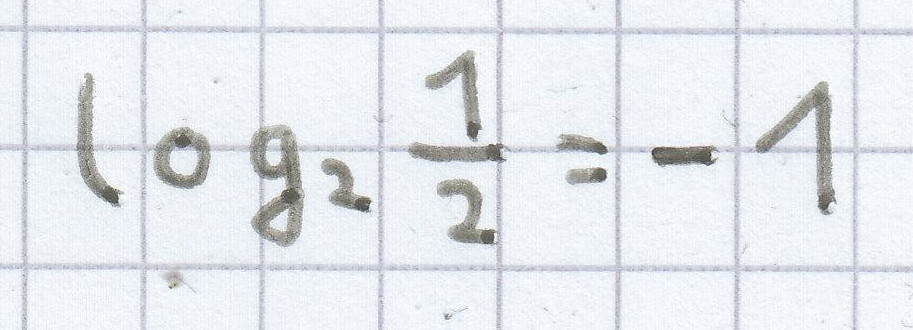
entspricht:
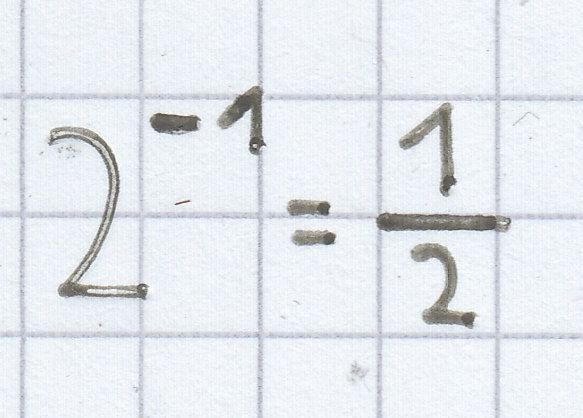
2.2 Das Potenzieren und das Logarithmieren
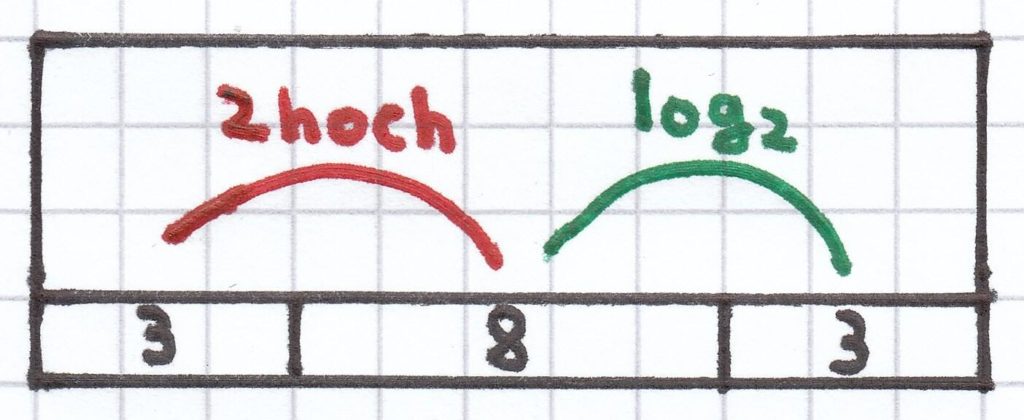
Gegenrechenoperation gegenseitig auf. Potenzieren und Logarithmieren als Gegenrechenoperationen
In Worten wiedergegeben: Die Basis 2 mit dem Exponenten 3 ergibt 8 (Potenziere 2 hoch 3). Der Logarithmus zur Basis 2 ergibt den Numerus 3 (Logarithmiere 2 von 8).
Das Logarithmieren zu Basis b ist die Gegenrechenoperation des Potenzierens zur Basis b.
Es gilt deshalb: logb bx = x für alle x Є ℝ
Beispiele:
23 = 8 entspricht: log2 8 = 3
24 = 16 entspricht: log2 16 = 4
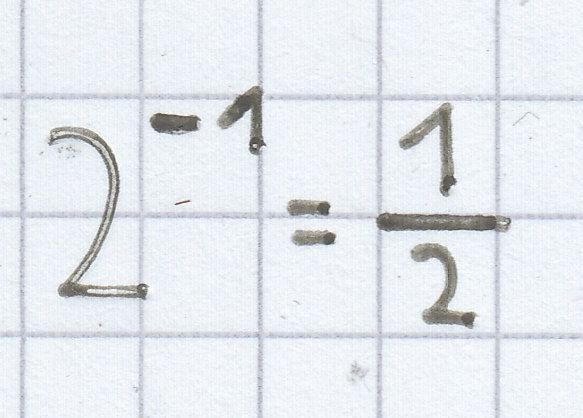
entspricht:
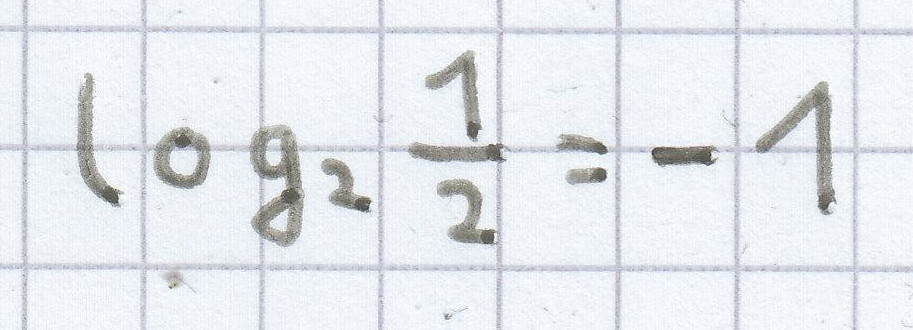
3. Die drei verschiedenen Aufgabenkonstellationen bei Logarithmen
Bei einem Logarithmus logb y = x kann je nach Aufgabe die Basis b gesucht sein, der Numerus y oder das x, der Exponent zur Basis b in der Potenzschreibweise.
3.1 Logarithmus mit x als Variable
Es ist folgende Logarithmus-Gleichung gegeben: log2 16 = x. Diese Gleichung löst man nun derart.
log2 16 = x
2x = 16
2x = 24
x = 4
Das x stellt in der Potenzschreibwese den Exponenten dar.
Beispiele:
a)
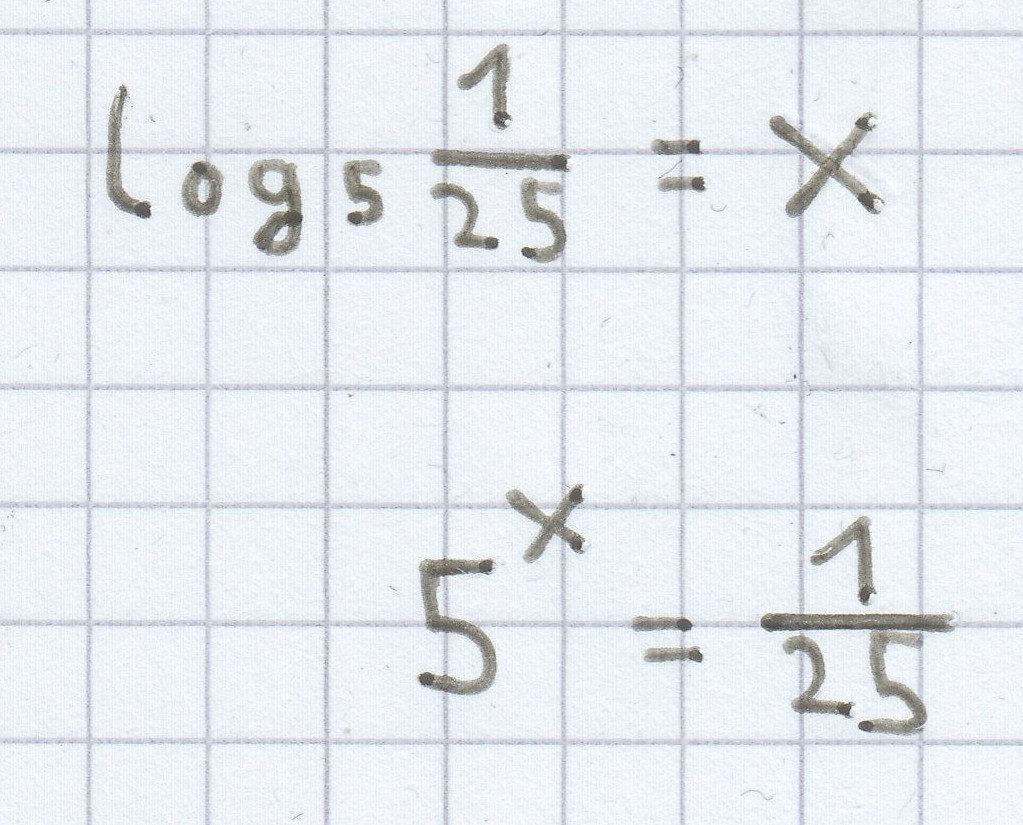
5x = 5–2
x = –2
b)
lg 0,001 = x
log10 0,001 = x
10x = 0,001
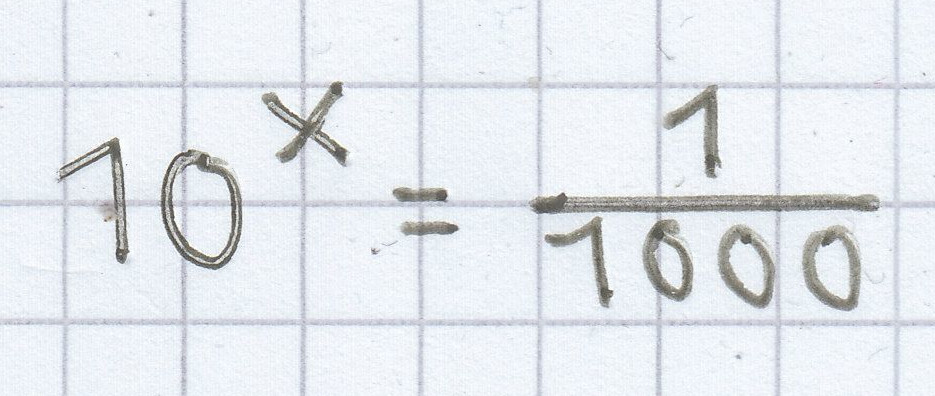
10x = 10–3
x = –3
3.2 Logarithmus mit Basis b als Variable
Es ist folgender Logarithmus gegeben: logb 64 = 3. Auf diese Weise löst man nun die Gleichung auf.
logb 64 = 3
b3 = 64
b3 = 43
b = 4
Beispiele:
a)
logb 4 = 1
b1 = 4
b1 = 41
b = 4
b)
logb 1024 = 5
b5 = 1024
b5 = 45
b = 4
3.3 Logarithmus mit Numerus y als Variable
Es ist dieser Logarithmus gegeben: log2 y = 5. Den Numerus y ermittelt man nun derart.
log2 y = 5
25 = y
y = 32
Beispiele:
a)
log2 y = 3
23 = y
y = 8
b)
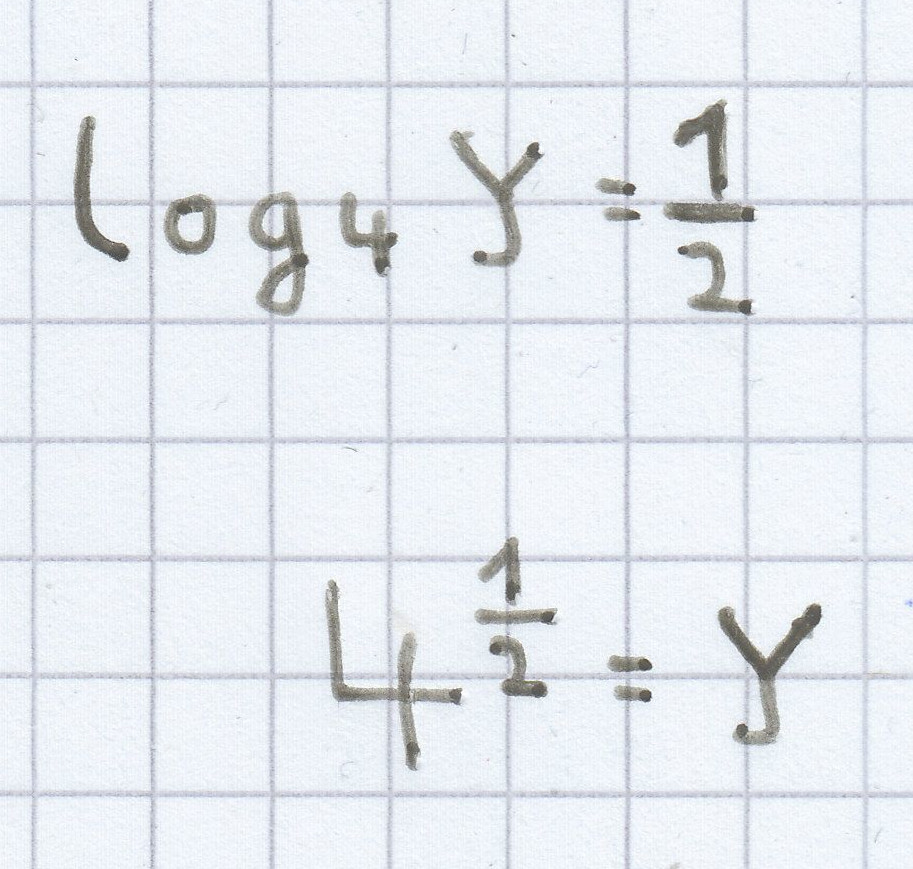
Logarithmus als Potenz
y = 2