
Ein Logarithmus kann in Mathe ja stets mit folgender Gleichung wiedergegeben werden logb y = x. Hierbei stellt b die Basis und y den Numerus des Logarithmus dar. Das x ist der Exponent, mit dem man die Basis b potenzieren muss, um den Numerus y bestimmen zu können. Aufgrund des Aufbaus einer Logarithmus-Gleichung ergeben sich drei verschiedene Aufgaben-Typen – je nach gesuchter Variable. Denn je nach Aufgabe kann bei der Gleichung das x gesucht sein, das b oder das y. Beim Lösen der gesuchten Variable muss man sich hierbei stets die Wechselbeziehung des Logarithmus zu folgender Potenzschreibweise vor Augen führen: logb y = x entspricht: bx = y. Dann kann man auch in Mathe ohne allzu große Schwierigkeiten diese höhere Rechenoperation meistern.
Aufgaben zum Mathematik-Stoffgebiet Logarithmen
1. Mathe-Nachhilfe-Aufgabe: Löse den Logarithmus auf.
a)

b)

c) log4 256
d) lg 10
e) log5 1
f) log4 45
2. Mathematik-Nachhilfe-Aufgabe: Bestimme zwischen welchen beiden ganzen Zahlen der Logarithmus sich befindet.
a) log4 13
b) log6 99
c) lg 29,5
d)

3. Mathe-Nachhilfe-Aufgabe: Ermittle die Variable.
a) logb 343 = 3
b) log2 y = 5
c) lg 1000 = x
d) logb 125 = 3
e) log8 2 = x
f) lg y = 6
g) lg y = 3
h) logb 8 = 3
i) log6 1296 = x
4. Mathematik-Nachhilfe-Aufgabe: Bestimme für den Term die Lösung.
a)

b)

c)

d) loga a2
e)

Lösungen zum Mathe-Stoffgebiet Logarithmen
1. Mathematik-Nachhilfe-Aufgabe: Ermittle das Ergebnis des Logarithmus.
a)


entspricht:

; Lösung: 3–4 =
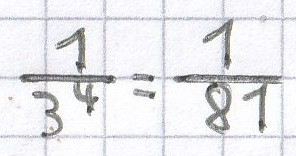
; x = –4
b)


entspricht:

; Lösung: 2–3 =
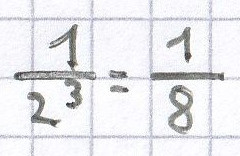
; x = –3
c) log4 256
log4 256 entspricht: 4x = 256; Lösung: 44 = 256; x = 4
d) lg 10
lg 10 entspricht: 10x = 10; Lösung: 101 = 10; x = 1
e) log5 1
log5 1 entspricht: 5x = 1; Lösung: 50 = 1; x = 0
f) log4 45
log4 45 entspricht: 4x = 45; Lösung: 45 = 45; x = 5
2. Mathe-Nachhilfe-Aufgabe: Ermittle zwischen welchen beiden ganzen Zahlen der Logarithmus liegt.
a) log4 13
log4 13 entspricht: 4x = 13
41 = 4; 42 = 16; der Logarithmus liegt zwischen den Zahlen 1 und 2.
b) log6 99
log6 99 entspricht: 6x = 99
62 = 36; 63 = 216; der Logarithmus befindet sich zwischen den Zahlen 2 und 3.
c) lg 29,5
lg 29,5 entspricht: 10x = 29,5
101 = 10; 102 = 100; der Logarithmus liegt zwischen den Zahlen 1 und 2.
d)


entspricht:

;
2–2 =

; 2–1 =
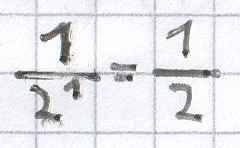
; der Logarithmus liegt zwischen den Zahlen –2 und –1.
3. Mathematik-Nachhilfe-Aufgabe: Ermittle die Variable.
a) logb 343 = 3
logb 343 = 3 entspricht: b3 = 343; Lösung: 73 = 343; b = 7
b) log2 y = 5
log2 y = 5 entspricht: 25 = y; Lösung: 25 = 32; y = 32
c) lg 1000 = x
lg 1000 = x entspricht: 10x = 1000; Lösung: 103 = 1000; x = 3
d) logb 125 = 3
logb 125 = 3 entspricht: b3 = 125; Lösung: 53 = 125; b = 5
e) log8 2 = x
log8 2 = x entspricht: 8x = 2;
Lösung:

;

f) lg y = 6
lg y = 6 entspricht: 106 = y; Lösung: 106 = 1000000; y = 1000000
g) lg y = 3
lg y = 3 entspricht: 103 = y; Lösung: 103 = 1000; y = 1000
h) logb 8 = 3
logb 8 = 3 entspricht: b3 = 8; Lösung: 23 = 8; b = 8
i) log6 1296 = x
log6 1296 = x entspricht: 6x = 1296; Lösung: 64 = 1296; x = 4
4. Mathe-Nachhilfe-Aufgabe: Ermittle die Lösung des Terms.
a)


entspricht:

;
Lösung:

;
5x = 5-m; x = –m
b)


entspricht:
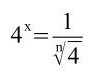
;
Lösung:
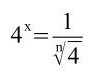
;

;

;
Lösung:

c)


entspricht:

;
Lösung:

;

;

;

;
Lösung:

d) loga a2
logaa2 entspricht: ax = a2; Lösung: x = 2
e)


entspricht:

;
Lösung:
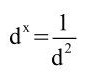
;
dx = d-2; x = –2