Kategorie: Lineare Gleichungen

Kategorien
Funktionen Gleichungen Lineare Funktionen Lineare Gleichungen Mathe Mathematik Nachhilfe

Mathematik-Nachhilfe: Aufgaben zu linearen Funktionen, Teil 3

Eine Funktion in Mathe © Samuel-G. / PIXELIO

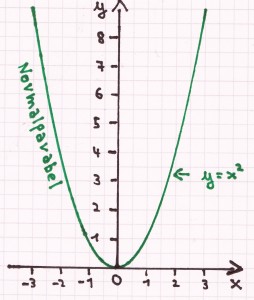
Beim Stoffgebiet lineare Funktionen in Mathe lernt man bereits, dass bei Funktionen sowohl immer rechnerisch als auch zeichnerisch Funktionsuntersuchungen gemacht werden können. Lineare Funktionen weisen ja auch, wie alle anderen Funktionen, bestimmte Merkmale/Charakteristika auf. So sind lineare Funktionen beispielsweise normalerweise linear steigend oder fallend (das kann man anhand der Funktionsgleichung ablesen) und sie haben einen Schnittpunkt mit der x und y-Achse (das kann man beides rechnerisch bestimmen). Der Graph einer linearen Funktion ist hierbei eine Gerade – die dann ebenfalls alle Merkmale/Charakteristika aufweist, welche man rechnerisch bestimmt hat oder bestimmen kann. Aus diesem Grund sind im Fach Mathematik lineare Funktionen auch sehr wichtig, da sie zur Gänze bereits darlegen, was das Besondere an ihnen ist. Bei anderen Funktionen verhält es sich dann genauso.

Weiterlesen „Mathematik-Nachhilfe: Aufgaben zu linearen Funktionen, Teil 3“
Kategorien
Gleichungen Lineare Gleichungen Mathe Mathematik Nachhilfe

Mathematik-Nachhilfe: Aufgaben zu linearen Gleichungen, Teil 6

Fundamentale (Bau-)Prinzipien bei Bauklötzen © Daniel Bleyenberg / PIXELIO

Inzwischen bereits ein Dauerthema im Mathematik Nachhilfe Blog stellen lineare Gleichungen dar. Das hat natürlich seine Gründe und ist demzufolge alles andere als grundlos. Außenstehende können nämlich sofort immer das Argument anführen, dass man durch das Ständig-Gleiche ja nichts Neues lernt! IMMER wieder lineare Gleichungen – ist ja auch immer wieder dasselbe. Es gibt hierfür aber dennoch folgende überaus plausible Gründe: Lineare Gleichungen sind die ersten in Mathe thematisierten Gleichungen. Sie stellen daher das Fundament für alle weiteren in Mathematik noch behandelt werdenden Gleichungen dar; die dort thematisierten algebraischen Gesetzmäßigkeiten sind daher auch Fundamentalgesetzmäßigkeiten/Fundamentalprinzipien; lineare Gleichungen weisen bereits viele verschiedene Aufgabentypen auf, die bei komplexeren Aufgaben wiederum auftreten; lineare Gleichungen sind sehr wichtig allgemein für das Verständnis von Gleichungen und Funktionen. Außerdem ist das hier ein Mathematik Nachhilfe Blog 😉 , die Wiederholung, die Repetitio, ist Blog-immanent 😉 .

Weiterlesen „Mathematik-Nachhilfe: Aufgaben zu linearen Gleichungen, Teil 6“
Kategorien
Funktionen Gleichungen Lineare Funktionen Lineare Gleichungen Mathe Mathematik Nachhilfe

Mathematik-Nachhilfe: Aufgaben zu quadratischen Funktionen, Teil 2

Die Normalparabel

Der bekannteste Graph einer quadratischen Funktion ist die sogenannte Normalparabel. Da es hierfür in Mathe extra eine Schablone gibt, kennt man die Normalparabel normalerweise sehr gut – und deren möglichen Verläufe im Koordinatensystem. Hierfür muss man sich zuvor nur die quadratischen Funktionen genau anschauen. Dann weiß man auch, wo man die Normalparabel im Koordinatensystem einzeichnen muss. Man orientiert sich hierbei an der Funktion y = x². Das stellt die nach oben geöffnete Normalparabel, vom Koordinatenursprung ausgehend, dar. Heißt die Funktion jedoch y = x² + 4, so muss man die Funktion um vier Längeneinheiten nach oben verschieben (entlang der y-Achse). Bei der Funktion y = (x – 4)² um vier Längeneinheiten nach rechts (entlang der x-Achse). Bei der Funktion y = (x – 4)² + 4 um vier Längeneinheiten nach rechts und vier Längeneinheiten nach oben.

Weiterlesen „Mathematik-Nachhilfe: Aufgaben zu quadratischen Funktionen, Teil 2“
Kategorien
Funktionen Gleichungen Lineare Funktionen Lineare Gleichungen Mathe Mathematik Nachhilfe

Mathematik-Nachhilfe: Aufgaben zum Stoffgebiet Funktionen, Teil 1

Graphen von Funktionen und andere Darstellungen im Fach Mathematik

Neben Gleichungen sind in Mathe ebenso Funktionen überaus wichtig. Beides bedingt sich ja. Eine Funktion kann ja immer auch mittels einer Gleichung wiedergegeben werden. Eine Funktion weist hierbei immer folgende Merkmale auf: Sie hat eine Definitionsmenge, eine Zuordnungsvorschrift, eine Funktionsgleichung und einen Funktionsterm. Mittels einer Wertetabelle kann oft eine Funktion in ein Koordinatensystem gezeichnet werden. Das Schaubild im Koordinatensystem nennt man Graphen der Funktion. Eine der einfachsten Funktionen ist die erste Winkelhalbierende. Diese hat die Definitionsmenge D = ℝ, die Zuordnungsvorschrift x → x, die Funktionsgleichung y = x und der Funktionsterm ist x. Der Graph dieser Funktion ist eine Gerade. Das alles sollte man bei Funktionen sehr gut verinnerlicht haben, da in der Oberstufe in der Analysis nur Funktionen analysiert werden.

Weiterlesen „Mathematik-Nachhilfe: Aufgaben zum Stoffgebiet Funktionen, Teil 1“
Kategorien
Gleichungen Lineare Funktionen Lineare Gleichungen Mathe Mathematik Nachhilfe

Mathematik-Nachhilfe: Aufgaben zu linearen Funktionen, Teil 1

Zwei parallel verlaufende – dicke – Geraden © RoKnoFoto PIXELIO www.pixelio.de

Die ersten in Mathe dran kommenden Funktionen sind lineare Funktionen.

Diese haben folgende Zuordnungsvorschrift:

x ↦ m · x + n

und diese Funktionsgleichung:

y = m · x + n.

Wie man sieht, weisen lineare Funktionen in der Regel eine Variable/„x“ auf, die die Potenz hoch eins/„x“ bzw. „x¹“ besitzt. Darüber hinaus einen konstanten Wert/„m“, der mit der Variablen verbunden ist. „m“ ist hierbei die Steigung der linearen Funktion. Ebenso besitzen lineare Funktionen oftmals einen zweiten konstanten Wert, nämlich „n“. „n“ wird hierbei als das absolut Glied bezeichnet und ist der Ordinatenabschnitt, also der Schnittpunkt mit der y-Achse. Hat man die Funktionsgleichung einer linearen Funktion gegeben, so kann man diese immer sofort in ein Koordinatensystem einzeichnen. Der Graph der so dargestellten linearen Funktion ist hierbei immer eine Gerade.

Weiterlesen „Mathematik-Nachhilfe: Aufgaben zu linearen Funktionen, Teil 1“