Der Satz des Pythagoras stellt eine Flächengleichung dar. Das lernt man am Anfang, wenn man mit dem Satz des Pythagoras in der Schule erstmalig zu tun hat – das vergisst man aber darauf oft recht schnell. Denn man wendet dann nur noch die Gleichung des Satz des Pythogras an, ohne genau mehr zu wissen, worauf diese basiert. Das ist aber nicht weiter schlimm. Schließlich kommt es letztlich darauf an, diese Flächengleichung richtig anzuwenden – und hierfür gibt es hier zahlreiche Übungsaufgben zum Satz des Pythagoras.
Diese Übungsaufgaben eigenen sich für Klassen ab der Mittelstufe bis zum Abitur, für Realschulen, Gesamtschulen, Gemeinschaftschulen und Gymnasien.
Aufgaben Satz des Pythagoras
1. Es ist ein rechtwinkliges Dreieck mit der Hypotenuse c = 17 cm und einer Kathete a = 8 cm gegeben. Wie groß ist die zweite Kathete?
Berechne auch:
c = 10 cm, a = 6 cm; c = 20 cm, a = 12 cm; c = 25 cm, a = 7 cm; c = 15 cm, a = 9 cm
2. Prüfe rechnerisch, ob hier ein rechwinkliges Dreieck vorliegt.
a) a= 9 cm, b = 12 cm, c = 15 cm b) a = 5 cm, b = 12 cm, c = 13 cm
c) a = 6 cm, b = 7 cm, c = 10 cm d) a = 7 cm, b = 24 cm, c = 25 cm
e) a = 10 cm, b = 10 cm, c = 14 cm
3. Es ist ein rechwinkliges Dreieck ABC mit γ = 90° gegeben. Berechne die fehlende Dreiecksseite.
a) a = 9 cm b) a = 7 cm c) b = 24 cm d) a = 5 cm e) a = 15 cm
b = 12cm c = 25 cm c = 26 cn b = 13 cm b = 17 cm
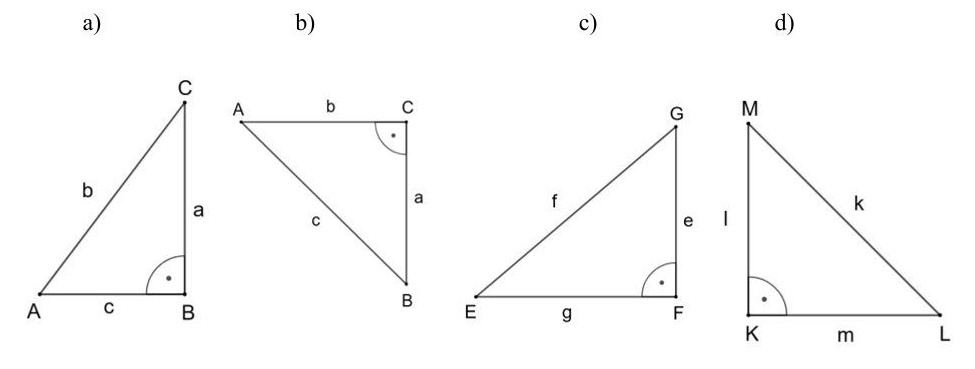
4. Es sind verschiedene rechtwinklige Dreiecke gegeben. Gib für die Dreiecke jeweils die Gleichung nach dem Satz des Pythagoras an.