
Liebe Leser,
mein Name ist Thorsten Schulz und ich bin zertifizierter Nachhilfe-Lehrer in Hannover, Umgebung und online weltweit. In diesem Gastbeitrag von mir soll es um den Stoff gehen, der in der Mathematik geformt wird, also die Zahlen. Genauer gesagt: Mengen von Zahlen. Mehr Informationen über mich und meine Arbeit finden Sie unter Online-Nachhilfe Hannover.
Jeder von uns weiß, was eine Menge ist. Im US-Film Rainman von 1988 hat der Autist Raymond, gespielt von Dustin Hoffmann, blitzschnell eine Menge Zahnstocher gezählt, die eine Serviererin versehentlich fallen ließ.
Im Unterschied hierzu besteht eine Zahlenmenge aus einzigartigen Elementen. Ein Element darf somit nur einmal innerhalb einer Menge vorkommen. In der Mathematik gibt es also nicht die Menge {1, 2, 2, 4, 5}, sondern die korrekte Notation wäre dann {1, 2, 4, 5}, wobei {2, 1, 5, 4} ebenfalls korrekt wäre, denn die Reihenfolge spielt keine Rolle. Als Trennzeichen eignet sich übrigens auch das Semikolon, um Dezimalbrüche zu separieren: {1, 2; 5, 9; 3, 7}.
Eine Menge im mathematischen Sinne beschränkt sich allerdings nicht nur auf Zahlen. Der Vollständigkeit und Anschaulichkeit halber sei hier erwähnt, dass die Menge {rotes Auto, grünes Auto, blaue Tomate} ebenfalls mathematisch zulässig ist. Sie ist wieder identisch mit der Menge {grünes Auto, blaue Tomate, rotes Auto}.
Dennoch sind wohl die wichtigsten Mengen in der Mathematik die Zahlenmengen. Hier gibt es Gruppen, die sich bereits etabliert haben. Fängt ein Kind an zu zählen, beginnt es wahrscheinlich mit 1, 2, 3.

Natürliche Zahlen
Die Menge der positiven ganzen Zahlen wird mit ℕ bezeichnet, also ℕ = {1, 2, 3, 4,…, 10, …, 100, …}. Die Null gehört nicht dazu. Es handelt sich um die Menge der Natürlichen Zahlen und sie ist unendlich groß. Man kann sich das leicht vorstellen: Jede ganze Zahl kann ich größer machen, indem ich z. B. 1 hinzuaddiere oder eine Null anhänge. Das Symbol für die Menge der Natürlichen Zahlen einschließlich 0 ist ℕ0. Oft wird aber auch bei dem Symbol ℕ die Null hinzugezählt. Hier gibt es leider keine Übereinstimmung.
Ganze Zahlen
In der Menge der Ganzen Zahlen ist die Menge der Natürlichen Zahlen bereits enthalten. Hinzu kommt die Null und alle negativen ganzen Zahlen. Diese Menge wird mit ℤ bezeichnet, also ℤ = {…, –100, …, –1, 0, …, 5, …}. Auch sie und alle folgenden Zahlenmengen enthalten unendlich viele Elemente, denn die Natürlichen Zahlen sind überall vollständig enthalten und bereits ihre Menge ist unendlich groß.
Rationale Zahlen
Die Menge der Rationalen Zahlen ist die Menge der Ganzen Zahlen, erweitert um alle Brüche, die sich mithilfe ganzer Zahlen darstellen lassen. Also z. B.
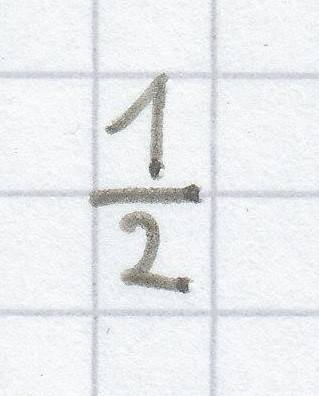
= 0,5 oder

= 0,33333… Symbol der Rationalen Zahlen ist ℚ.
Reelle Zahlen
Die Menge der Reellen Zahlen erweitert die Menge der Rationalen Zahlen auf der Zahlengeraden um alle Zahlen, die sich nicht mit einem Bruch darstellen lassen. Zum Beispiel gehören alle Zahlen dazu, die nicht periodisch sind und die unendlich viele Nachkommastellen haben, wie im Falle der Kreiszahl π. Zwischen jeweils zwei Elementen der Rationalen Zahlen gibt es unendlich viele weitere reelle Zahlen aus der Menge ℝ.
Komplexe Zahlen
Fügt man den Reellen Zahlen noch ein bestimmtes Element hinzu, erhält man die Menge der Komplexen Zahlen. Dieses Element wird mit i bezeichnet und ist die Wurzel aus –1, sodass i2 = –1 ist. In der Realschule gilt x2 = –1 als nicht lösbar, weil dort nur eine Lösung innerhalb der Menge der Reellen Zahlen gesucht wird. Symbol der Komplexen Zahlen ist ℂ.