Eine quadratische Gleichung hat ja als Lösungen entweder zwei Lösungen, eine Lösung oder keine Lösung. Fast bis zum Erbrechen überprüft man dies rechnerisch bei unzähligen quadratischen Gleichungen. Das hat auch mit den verschiedenen rechnerischen Lösungsverfahren zu tun, die man hier immer auch anwenden muss – und beim Lösen der quadratischen Gleichungen mitlernt. So weiß man, dass man die p-q-Formel und das quadratische Ergänzen jeweils zum rechnerischen Lösen einer quadratischen Gleichung heranziehen kann. Ebenso wissen ältere Semester, dass das auch über die sogenannte Mitternachtsformel funktioniert. Aufgrund des vielen Rechnens vergisst man hierbei aber, dass man jede quadratische Gleichung auch zeichnerisch lösen kann. Zugegebenermaßen ist das zwar mühsamer und ungenauer als die rechnerischen Lösungsverfahren – aber es bringt einem noch einmal entschieden den Aufbau quadratischer Gleichungen näher.
Aufgaben zum Mathematik Stoffgebiet Quadratische Gleichungen
1. Mathe-Nachhilfe-Aufgabe: Ziehe eine Tabelle heran, um Zahlen zu ermitteln, deren Quadrat
a) genauso groß ist wie das 6-Fache der Zahl verringert um 8;
b) gleich der Differenz aus 16 und dem 1,8-Fachen der Zahl;
c) die Hälfte beträgt, wie das 3-Fache der Zahl um 20 vermehrt.
2. Mathematik-Nachhilfe-Aufgabe: Lege eine Tabelle an für die Lösungsmenge der quadratischen Gleichung (Grundmenge G = ℤ). Hierbei soll auf einer Seite der Gleichung das quadratische Glied ohne Faktor stehen, auf der anderen Seite der Gleichung das lineare Glied und das absolute Glied.
a) 2x² + 16x + 32 = 0
b) x² – 2x – 15 = 0
c) 0,5y² + y = 0
d) 0,5x² – 1,5x – 2 = 0
3. Mathe-Nachhilfe-Aufgabe: Bestimme zeichnerisch die Lösung der quadratischen Gleichung.
a) x² – 2x + 1 = 0
b) x² – 2x – 8 = 0
c) x² + 1 = 0
d) x² – 2 = 0
4. Mathematik-Nachhilfe-Aufgabe: Wie fit bist du bei quadratischen Gleichungen? Ermittle, ob eine quadratische Gleichung vorliegt. Wenn ja, bestimme, ob diese rein- oder gemischtquadratisch ist.
a) x² – 7 = 7
b) 9 = x²
c) 3y² = y – 5
d) 8a = a²
e) 2,5² = 8x
f) 8y + 6 = 3y
g) 4y + 7 – y² = 12
h) (5x – 4)² = 100
i) a – a² = 12
j) 3x² + 2x + 4x³ = 8
Lösungen zum Mathe-Stoffgebiet Quadratische Gleichungen
1. Mathematik-Nachhilfe-Aufgabe: Stelle eine Tabelle auf, um Zahlen zu bestimmen, deren Quadrat
a) genauso groß ist wie das 6-Fache der Zahl verringert um 8;
b) gleich der Differenz aus 16 und dem 1,8-Fachen der Zahl;
c) die Hälfte beträgt, wie das 3-Fache der Zahl um 20 vermehrt.
Bevor man eine Tabelle erstellt, sollte man die Gleichung für die jeweilige Aufgabe aufstellen!
a) x² = 6x – 8
In Worten: Das Quadrat einer Zahl entspricht dem 6-Fachen der Zahl verringert um 8. Tabelle planmäßiges Probieren Aufgabe a)
Planmäßiges Probieren führt hier zur Lösung des Zahlenrätsels. Wie man anhand der Tabelle sieht, nimmt bei zunehmenden x-Werten die Differenz zwischen den Term-Werten von x² und 6x – 8 ab (x = 0; x = 1). Bei x = 2 sind die Term-Werte gleich. Bei x = 3 besteht wieder eine Differenz. Bei x = 4 sind beide Term-Werte wiederum gleich.
Wie das planmäßige Probieren hier anhand der Tabelle zeigt, ergibt sich für die Aufgabe a) die Lösung x1 = 2, da hier bei den Termen x² und 6x – 8 der Term-Wert jeweils 4 ist.
Ebenfalls eine Lösung des Zahlenrätsels ist x2 = 4, da hier bei den Termen x² und 6x – 8 der Term-Wert jeweils 16 ist.
L = {2; 4}
b) x² = 16 – 1,8x
In Worten: Das Quadrat der Zahl entspricht 16 weniger dem 1,8-Fachen der Zahl Tabelle planmäßiges Probieren Aufgabe b)
Wie man hier sieht, besteht bei x = –6 eine Differenz zwischen dem Term-Wert von x² und 16 – 1,8x. Bei x = –5 sind beiderseitige Term-Werte gleich. Daraufhin besteht wiederum eine Differenz, die am geringsten bei dem x-Werte x = 3 ist. Bei x = 4 nimmt die Differenz wieder zu. Darauf ergibt sich, dass zwischen x = 3 und x = 4 eine weitere Lösung des Zahlenrätsels liegen muss. Diese Lösung ist aber nicht ganzzahlig. Tabelle zweite Lösung Aufgabe b)
Wie die man hier sieht, ist ebenfalls x = 3,2 eine Lösung des Zahlenrätsels, da auch hier die Term-Werte von x² und 16 – 1,8x identisch sind.
L = {–5; 3,2}
c)
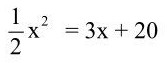
In Worten: Die Hälfte des Quadrats der Zahl ist gleich dem 3-Fachen der Zahl vermehrt um 20. Tabelle planmäßiges Probieren Aufgabe c)
Wie man hier sieht, ist x = –4 eine Lösung des Zahlenrätsels, da hier die Term-Werte von
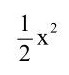
und 3x + 20 identisch sind. Alle Term-Werte bis x = 9 weisen eine Differenz auf. Erst bei x = 10 ergibt sich eine weitere Lösung des Zahlenrätsels, da hier wiederum die Term-Werte beider Terme gleich groß sind.
L = {–4; 10}
2. Mathe-Nachhilfe-Aufgabe: Mache eine Tabelle für die die Lösungsmenge der quadratischen Gleichung (Grundmenge G = ℤ). Auf der einen Seite der Gleichung soll hierbei das quadratische Glied ohne Faktor stehen, auf der anderen Seite der Gleichung das lineare und das absolute Glied.
a) 2x² + 16x + 32 = 0 | – 16x <=>
2x² + 32 = –16x | – 32 <=>
2x² = –16x – 32 | : 2 <=>

Wie man hier sieht, haben das quadratische Glied und das lineare und absolute Glied nur bei x = –4 den gleichen Term-Wert. Da das lineare Glied und das absolute Glied von x-Wert zu x-Wert sich um 8 verringert, gibt es sowohl im negativen als auch im positiven x-Werte-Bereich keinen gleich großen Term-Wert mehr zum quadratischen Glied. Im negativen x-Werte-Bereich hat das quadratische Glied viel höhere Term-Werte ab x = –5; im positiven x-Werte Bereich gibt es überhaupt keine Annäherung der Term-Werte mehr. Daher ist x = –4 die einzige Lösung der quadratischen Gleichung.
L = {–4}
b) x² – 2x – 15 = 0 | + 2x <=>
x² – 15 = 2x | + 15 <=>
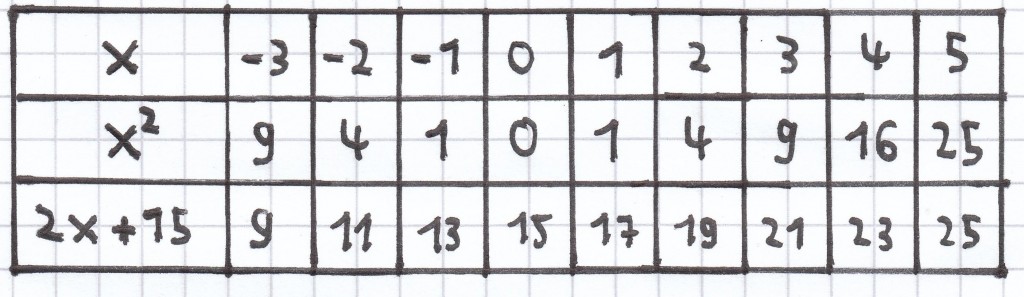
Wie man hier sieht, haben das quadratische Glied und das lineare und absolute Glied bei x = –3 und bei x = 5 die gleichen Term-Werte. Daher sind diese beiden x-Werte die Lösungen der quadratischen Gleichung.
L = {–3; 5}
c) 0,5y² + y = 0 | – y <=>
0,5y² = –y | · 2 <=>

Hier sieht man, dass bei x = –2 und bei x = 0 die Termwerte des quadratischen Gliedes und des linearen Gliedes (ein absolutes Glied tritt hier ja nicht auf) gleich groß sind. Daher sind dies hier die beiden Lösungen der quadratischen Gleichung.
L = {–2; 0}
d) 0,5x² – 1,5x – 2 = 0 | + 1,5x <=>
0,5x² – 2 = 1,5x | + 2 <=>
0,5x² = 1,5x + 2 | · 2 <=>

Wie man hier sieht, sind bei x = –1 und x = 4 die Termwerte des quadratischen Gliedes und des linearen und absoluten Gliedes identisch. Daher sind dies Lösungen der quadratischen Gleichung.
L = {–1; 4}
3. Mathematik-Nachhilfe-Aufgabe: Ermittle zeichnerisch die Lösung der quadratischen Gleichung.
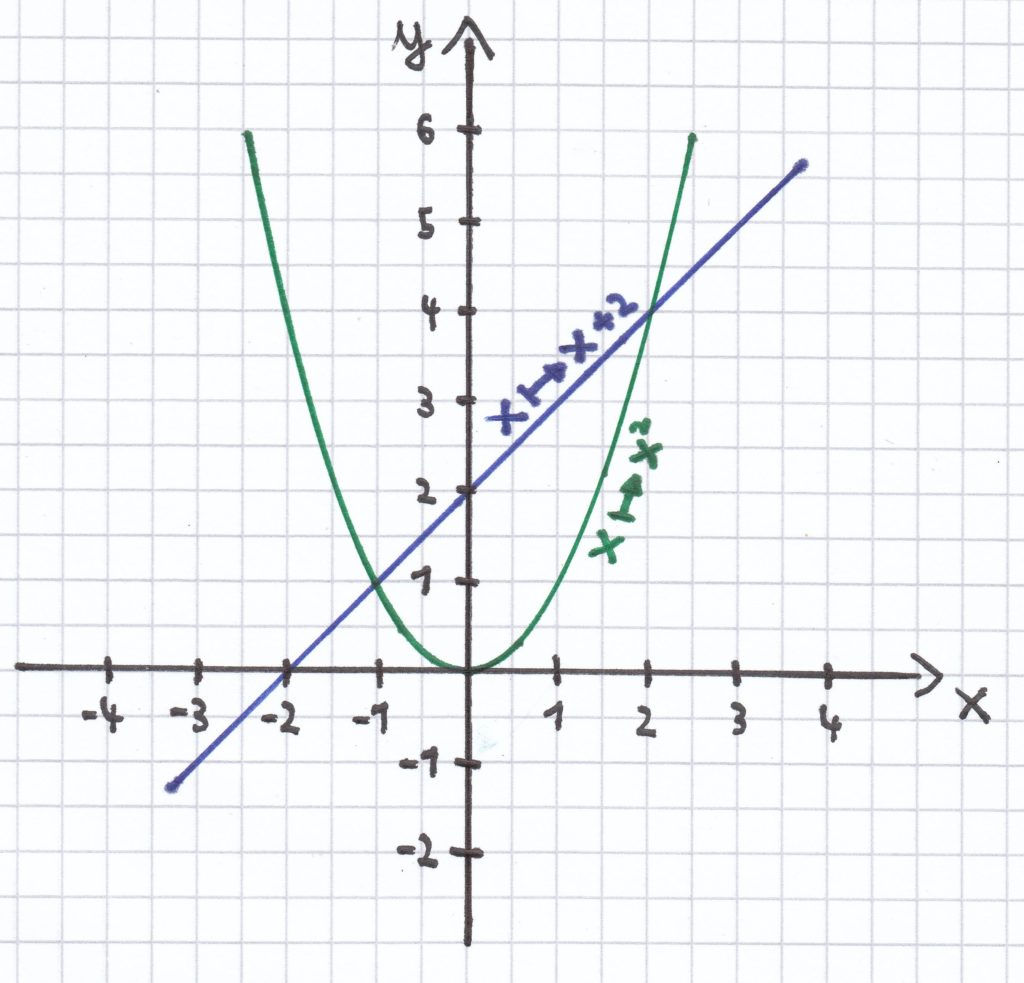
a) x² – 2x + 1 = 0 | + 2x <=>
x² + 1 = 2x | – 1 <=>
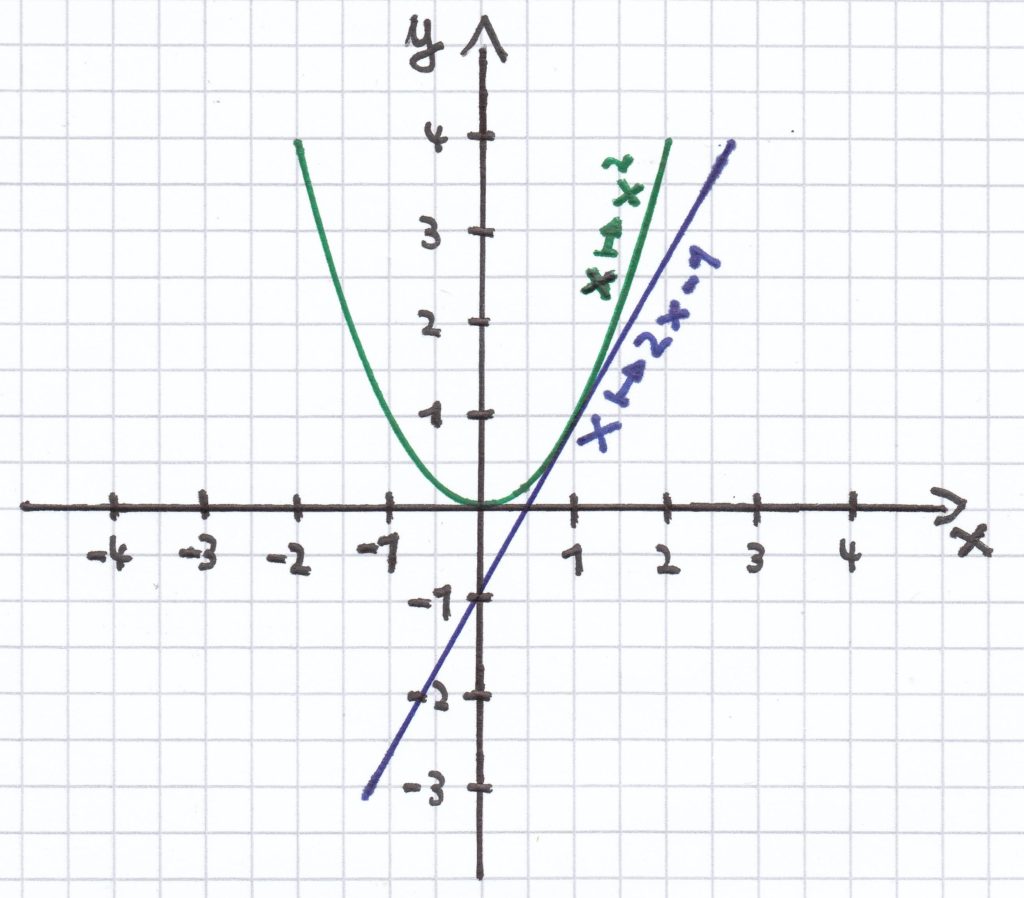
Wie man sieht, hat die Parabel mit der Geraden einen gemeinsam Schnittpunkt bzw. Berührpunkt bei P (1|1). Der x-Wert des gemeinsamen Punktes stellt hierbei eine Lösung der quadratischen Gleichung dar.
L = {1}
b) x² – 2x – 8 = 0 | + 2x <=>
x² – 8 = 2x | + 8 <=>
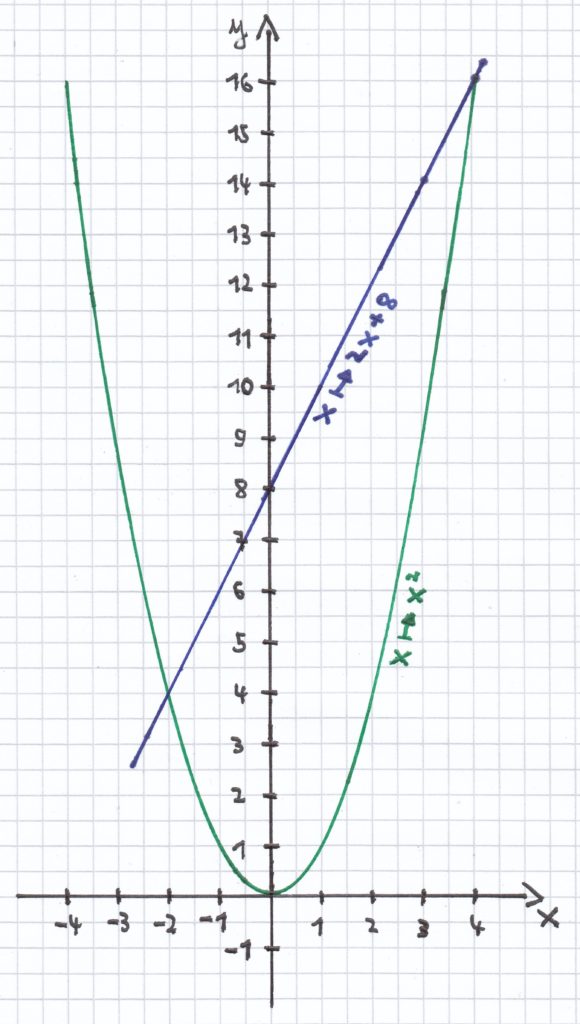
Wie man sieht, hat die Parabel mit der Geraden zwei Schnittpunkte. Der erste Schnittpunkt ist hierbei P1 (–2|4) und der zweite Schnittpunkt liegt bei P2 (4|16). Daher sind hier x1 = –2 und x2 = 4 die beiden Lösungen der quadratischen Gleichung.
L = {–2; 4}
c) x² + 1 = 0 | – 1 <=>
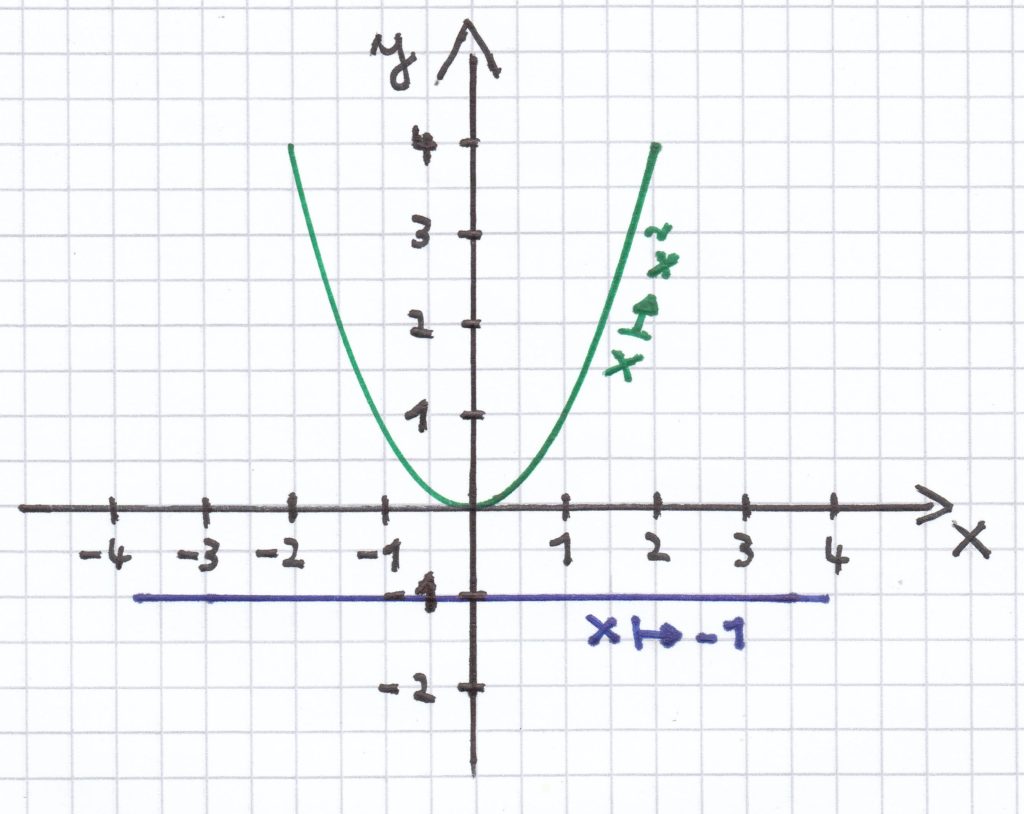
Wie man sieht, gibt es zwischen der Parabel und der Geraden keinen Schnittpunkt. Die quadratische Gleichung hat daher keine Lösung.
L = { } bzw. Ø
d) x² – 2 = 0 | + 2 <=>
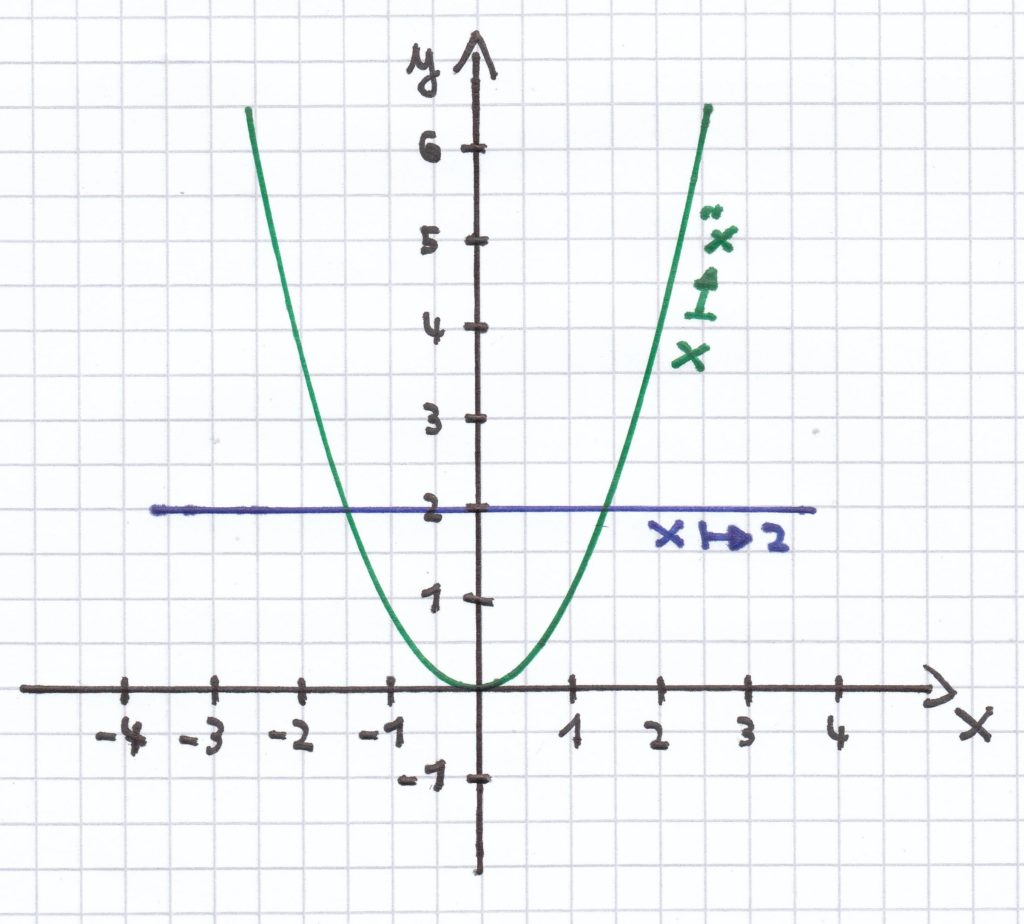
Wie man sieht, hat die Parabel mit der Geraden zwei Schnittpunkte. Da die Schnittpunkte keine ganzzahligen x-Werte vorweisen, sind diese nur annäherungsweise herauslesbar. Diese liegen in etwa bei P1 (–1,4|2) und der zweite Schnittpunkt liegt bei P2 (1,4|2). Die Lösungen der quadratischen Gleichung sind daher ungefähr x1 = –1,4 und x2 = 1,4.
L = {–1,4; 1,4}
4. Mathe-Nachhilfe-Aufgabe: Fit in quadratischen Gleichungen? Liegt tatsächlich eine quadratische Gleichung vor? Wenn ja, ist diese quadratische Gleichung reinquadratisch oder gemischtquadratisch.
a) x² – 7 = 7 | – 7 <=>
x² – 14 = 0
Da hier das lineare Glied fehlt, liegt hier eine reinquadratiche Gleichung vor.
b) 9 = x² | – 9 <=>
x² – 9 = 0
Hier liegt wiederum eine reinquadratische Gleichung vor.
c) 3y² = y – 5 | – y <=>
3y² – y = –5 | + 5 <=>
3y² – y + 5 = 0
Hier liegt eine gemischtquadratische Gleichung vor.
d) 8a = a² | – 8a <=>
a² – 8a = 0
Hier liegt ebenso eine gemischtquadratische Gleichung vor.
e) 2,5² = 8x <=>
6,25 = 8x | – 6,25 <=>
8x – 6,25 = 0
Hier liegt keine quadratische Gleichung vor, sondern eine lineare Gleichung.
f) 8y + 6 = 3y | – 3y <=>
5y + 6 = 0
Hier liegt wiederum eine lineare Gleichung vor.
g) 4y + 7 – y² = 12 | – 12 <=>
– y² + 4y – 5 = 0
Hier liegt eine gemischtquadratische Gleichung vor.
h) (5x – 4)² = 100 <=>
(5x)² + 2 · 5x · (–4) + (–4)² = 100
25x² – 40x + 16 = 100 | – 100 <=>
25x² – 40x – 84 = 0
Hier liegt wiederum eine gemischtquadratische Gleichung vor.
i) a – a² = 12 | – 12 <=>
–a² + a – 12 = 0
Hier handelt es sich wiederum um eine gemischtquadratische Gleichung.
j) 3x² + 2x + 4x³ = 8 | – 8 <=>
4x³ + 3x² + 2x – 8 = 0
Hier liegt eine ganzrationale Gleichung 3. Grades vor und daher keine quadratische Gleichung.