
Wenn ehemalige Schülerinnen und Schüler zu einer ganz bestimmten späteren Uhrzeit an Mathematik denken müssen – dann hat dies meist einen bestimmten Grund: Sie erinnern sich der großen Wichtigkeit einer Formel aus ihrem damaligen Mathe-Unterreicht – und zwar an die sogenannte Mitternachtsformel. Jeder, der früher Abitur gemacht hat, musste sich nämlich von seinem Mathe-Lehrer immer wieder gebetsmühlenartig anhören: „Diese Formel ist so wichtig, dass ihr sie sogar zu Mitternacht (und natürlich auch noch zu späterer Stunde 😉 ) auswendig vorsagen können müsst (und das, egal, wie euer geistiges und körperliches Befinden zu dieser Uhrzeit gerade ist 😉 )!“ Die Ergänzungen in der Klammer sind natürlich von mir spaßeshalber hinzugefügt worden, die Aussage des Lehrers entspricht jedoch einer wortwörtlichen Wiedergabe aus dem Mathe-Unterricht der Jahrzehnte vor dem 21. Jahrhundert. Denn noch vor der Schulreform und der damit einhergehenden Reform des Mathematik-Unterrichts hatte die Mitternachtsformel, mit der man die Lösungsmenge jeder quadratischen Gleichung der Form ax² + bx + c = 0 (a, b, x ∈ von und a ≠ 0) bestimmen kann, einen extrem hohen Stellenwert. Inzwischen sieht das jedoch fundamental anders aus!
Mittlerweile hat die „kleine Schwester“ der Mitternachtsformel nämlich im Mathe-Unterricht nicht nur viel, viel mehr an Ansehen gewonnen, sondern ihr sogar den Rang abgelaufen – die p-q-Formel. Der Grund hierfür liegt in der einfacheren Anwendbarkeit der pq-Formel begründet, da man diese ebenso zur Lösungsmengen-Bestimmung jeder quadratischen Gleichung heranziehen kann – hierbei aber mit p und q nur zwei konstante Werte vonnöten sind (anstatt mit a, b und c drei wie bei der Mitternachtsformel. Unerwähnt darf hierbei aber nicht bleiben, dass oftmals zur Anwendung der p-q-Formel erst noch eine Äquivalenzumformung gemacht werden muss, um einen etwaigen Faktor vor dem x² zu eliminieren – was aber kein großes Ding ist).

Aber auch wenn die p-q-Formel die „kleine Schwester“ von der Mitternachtsformel ist, so ist sie dennoch genauso wichtig, wie es ihre „ältere Schwester“ einst war. Schließlich verfolgen einen quadratische Gleichungen (und Funktionen) in Mathematik bis zum Abitur auf Schritt und Tritt. Daher ist es nicht nur Pflicht die p-q-Formel auswendig (und das am besten wie bei der Mitternachtsformel auch rund um die Uhr 😉 ) zu können, sondern natürlich diese auch stets fehlerfrei anwenden zu können.
Aufgaben zum Mathe-Stoffgebiet Quadratische Gleichungen
1. Mathematik-Nachhilfe-Aufgabe: Wende zur Ermittlung der Lösungsmenge die p-q-Formel an.
a) x² + 9x – 52 = 0
b) x² – 16x + 64 = 0
c) y² – 6y – 187 = 0
d) a² + 2,55a – 4,5 = 0
e) x² + 10,8x – 63 = 0
f) y² + 13y + 42,25 = 0
g) x² – 7x + 12 = 0
h) a² – 7a + 8 = 0
2. Mathe-Nachhilfe-Aufgabe: Bilde zu allen Aufgaben die Diskriminante. Lese davon ab, wie viele Lösungen die quadratische Gleichung hat und bestimme diese.
a) x² – 17x + 70 = 0
b) x² – 1,2x – 0,64 = 0
c) y² – 14x + 53 = 0
d) a² + 2,5a – 51 = 0
e) y² + 1,6x + 0,64 = 0
f)
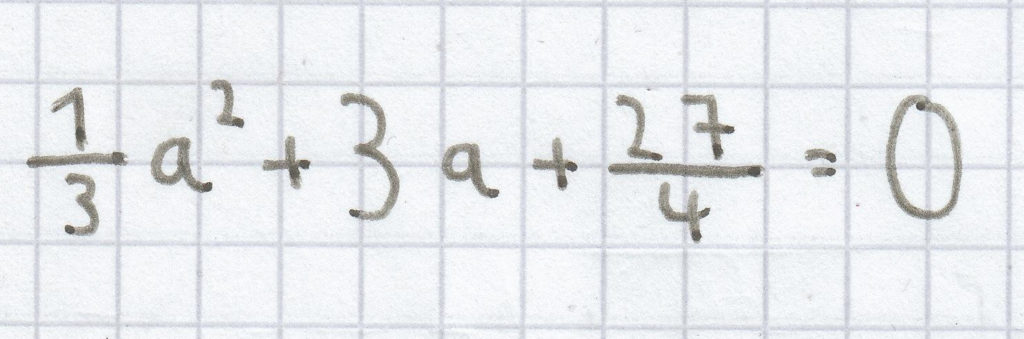
g) 10y² – 4x + 3 = 0
h) x² – 2,8x + 3,61 = 0
3. Mathematik-Nachhilfe-Aufgabe: Alle Gleichungen kann man in die Form x² + px = 0 auflösen. Ermittle anschließend die Lösung.
a) x (2x + 18) = 0
b) (8 + x) (4x – 6) = –48
c) (y – 10) (y – 5) = 50
d) (3x + 5) x + 1 = (2x + 1)²
e) (2a – 5) (5a – 2) = 10
f) 25 + 4x (2x + 1) = (5 + 3x)²
Lösungen zu dem Mathe-Stoffgebiet Quadratische Gleichungen
1. Mathe-Nachhilfe-Aufgabe: Löse die quadratischen Gleichungen mithilfe der p-q-Formel.
Die p-q-Formel lautet ja wie folgt:
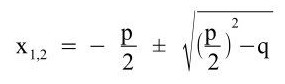
Zur Bestimmung der Lösungsmenge muss man nun bei jeder Aufgabe zuerst den p- und den q-Wert ermitteln und dann in die pq-Formel einsetzen.
Beim Einsetzen des p- und q-Wertes in die pq-Formel muss man immer besonders auf die Vorzeichenregel achten, dass „–“ und „–“ „+“ ergibt.
a) x² + 9x – 52 = 0
Bei dieser quadratischen Gleichung ist der p-Wert „9″ und der q-Wert „–52″.
Hier muss berücksichtigen, dass „–52″ zu „+52″ wird.
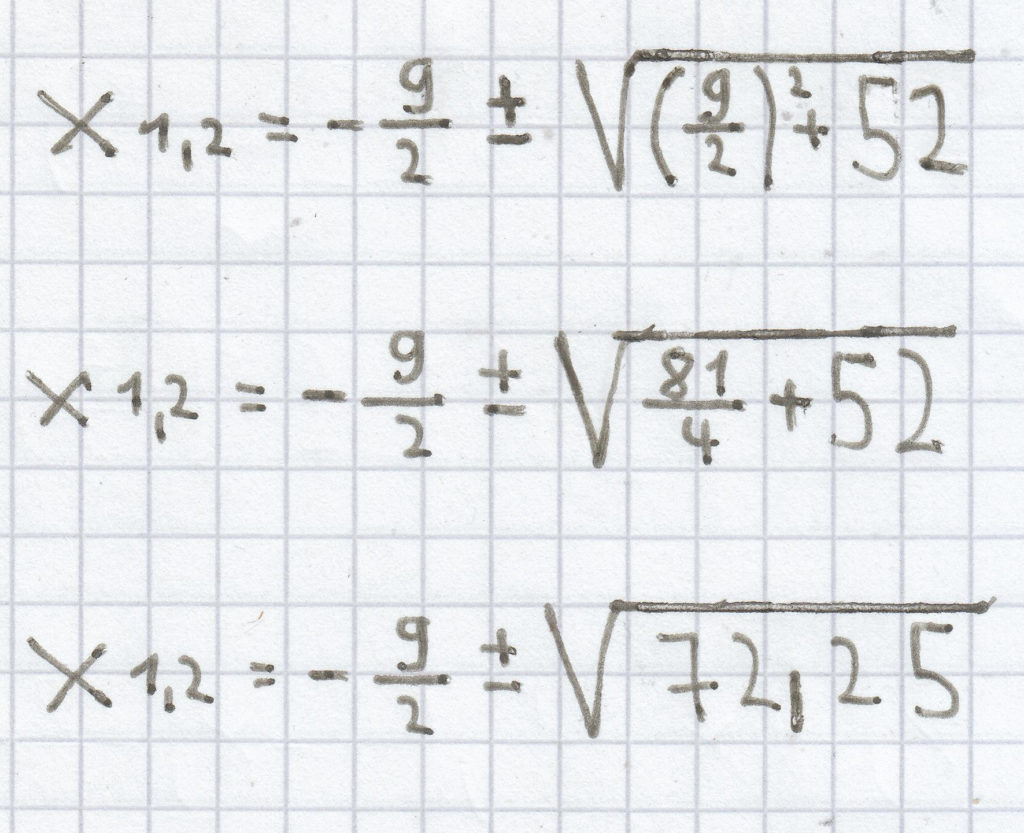
x1,2 = –4,5 ± 8,5
x1 = –4,5 – 8,5 = –13
x2 = –4,5 + 8,5 = 4
L = {– 13; 4}
b) x² – 16x + 64 = 0
Bei dieser quadratischen Gleichung ist „–16″ der p-Wert und „64″ der q-Wert.
Hier muss man beachten, dass „–16″ zu „+16″ wird.
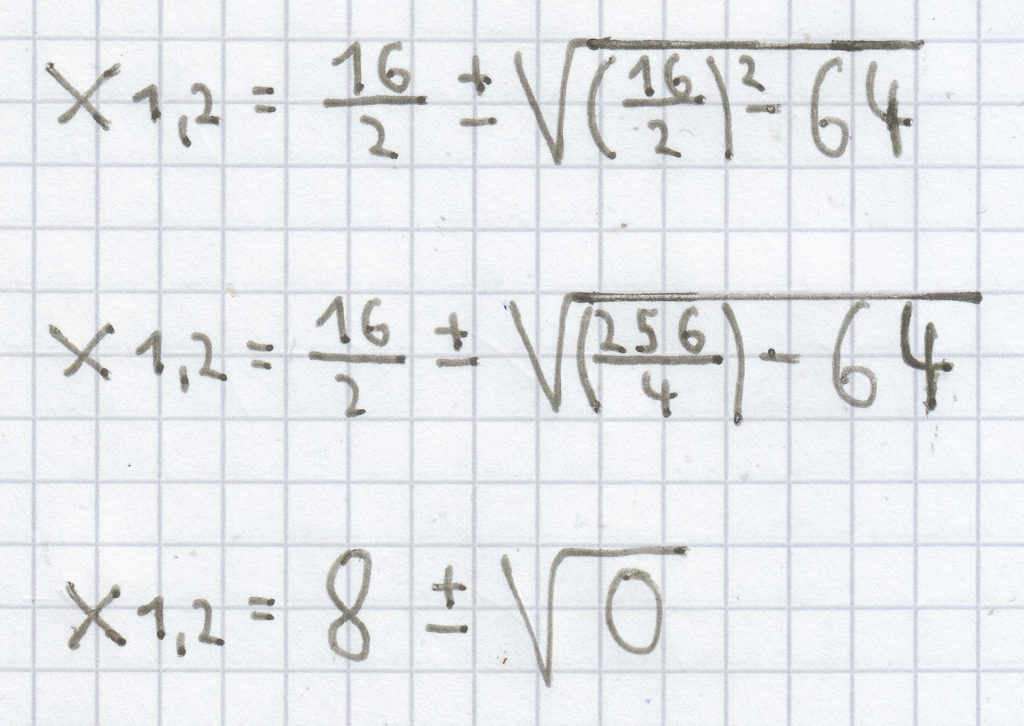
x1,2 = 8 ± 0
x1,2 = 8 ± 0 = 8
L = {8}
c) y² – 6y – 187 = 0
Bei dieser quadratischen Gleichung ist der p-Wert „–6″ und der q-Wert „–187″.
Hier muss man beachten, dass sowohl „–6″ zu „+6″ wird als auch „–187″ zu „+187″.
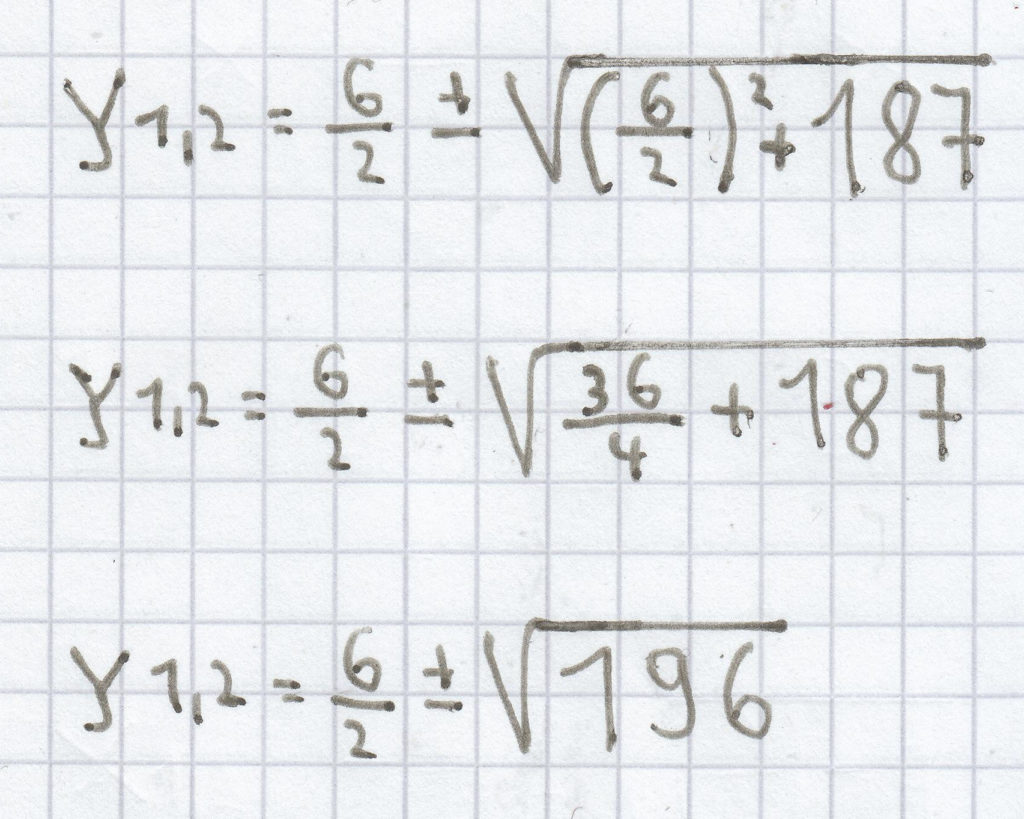
y1,2 = 3 ± 14
y1 = 3 – 14 = –11
y2 = 3 + 14 = 17
L = {– 11; 17}
d) a² + 2,55a – 4,5 = 0
Hier bei dieser quadratischen Gleichung ist der p-Wert „2,55″ und der q-Wert „–4,5″.
Wiederum gilt es hier zu beachten, dass „–4,5″ zu „+4,5″ wird.
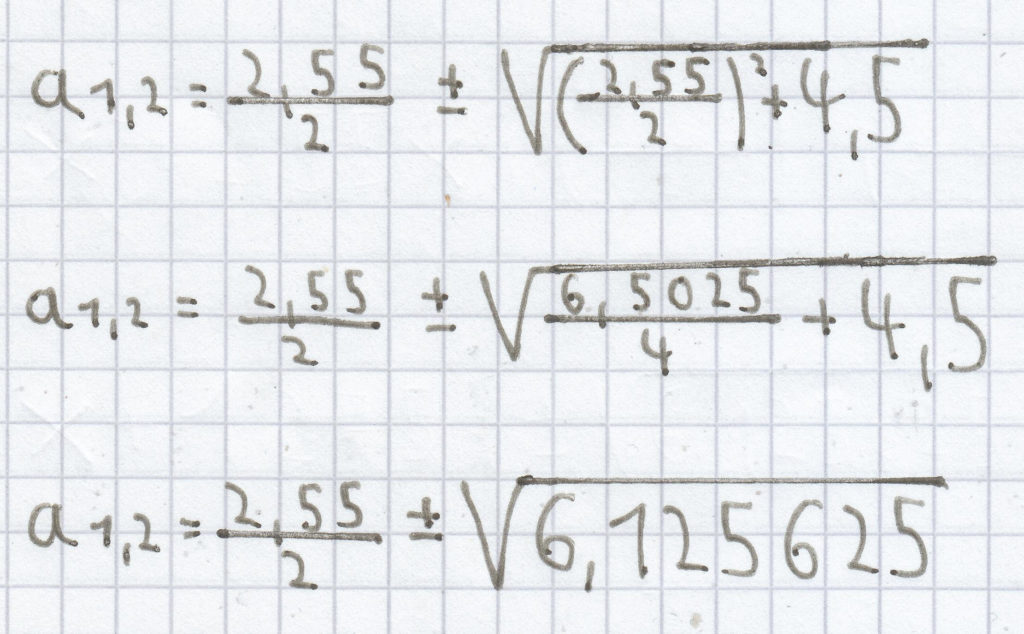
a1,2 = 1,275 ± 2,475
a1 = 1,275 – 2,475 = –1,2
a2 = 1,275 + 2,475 = 3,75
L = {– 1,2; 3,75}
e) x² + 10,8x – 63 = 0
Bei dieser quadratischen Gleichung ist der p-Wert „10,8″ und der q-Wert „–63″.
Hier gilt es zu beachten, dass „–63″ zu „+63″ wird.
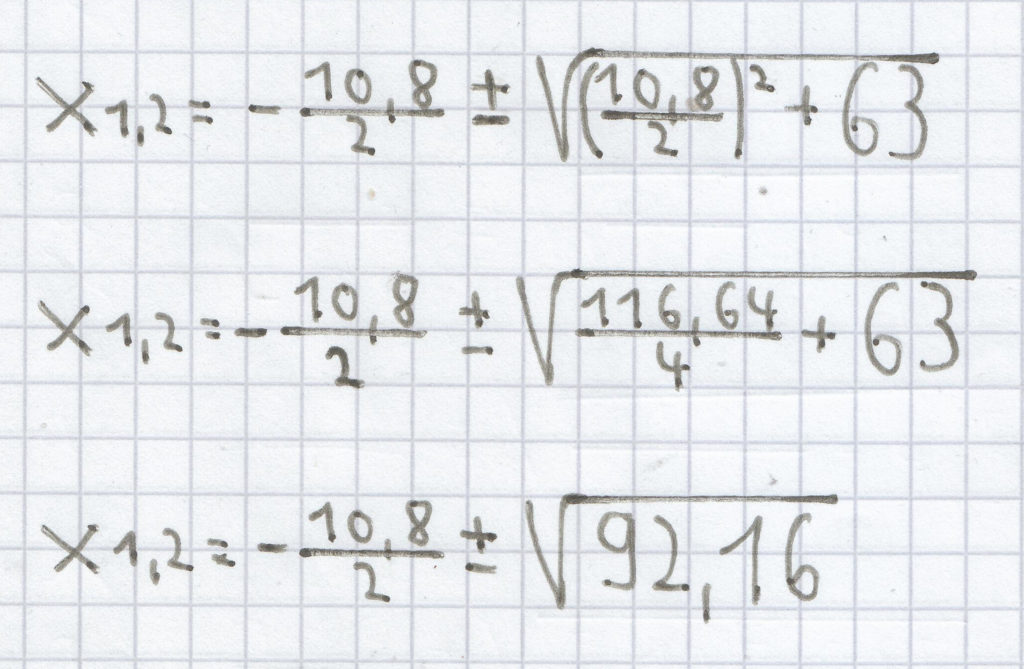
x1,2 = – 5,4 ± 9,6
x1 = –5,4 – 9,6 = –15
x2 = –5,4 + 9,6 = 4,2
L = {–15; 4,2}
f) y² + 13y + 42,25 = 0
Der p-Wert bei dieser quadratischen Gleichung ist „13″ und der q-Wert „42,5″.
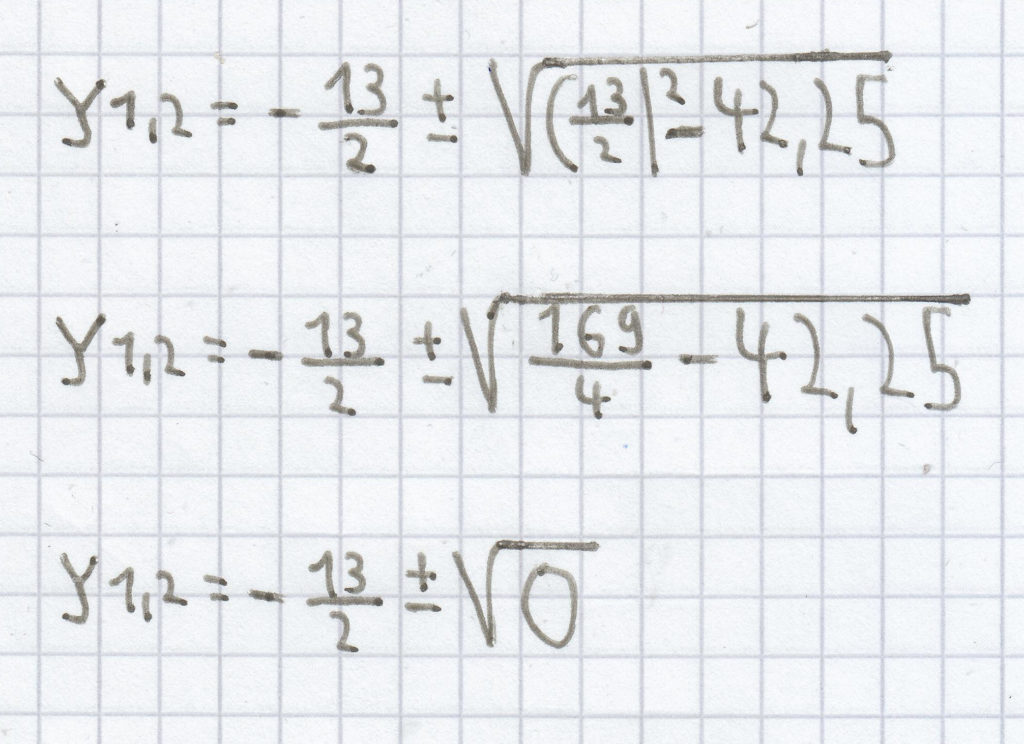
y1,2 = –6,5 ± 0
y1,2 = –6,5
L = {–6,5}
g) x² – 7x + 12 = 0
Bei dieser quadratischen Gleichung ist der p-Wert „–7″ und der q-Wert „12″.
Hier muss man die Vorzeichenregel beim p-Wert beachten, dass „–7″ zu „+7″ wird.
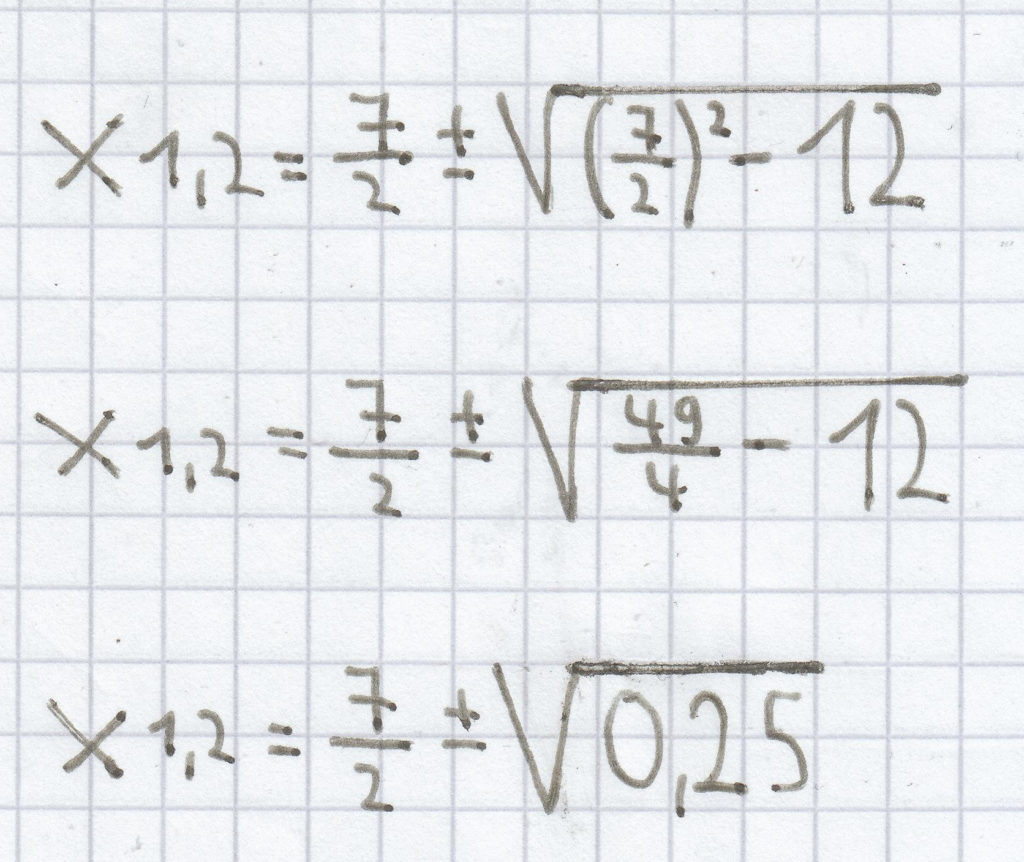
x1,2 = 3,5 ± 0,5
x1 = 3,5 – 0,5 = 3
x2 = 3,5 + 0,5 = 4
L = {3; 4}
h) a² – 7a + 8 = 0
Bei dieser quadratischen Gleichung ist der p-Wert „–7″ und der q-Wert „8″.
Hier muss man wiederum die Vorzeichenregehl beim p-Wert beachten, und zwar, dass„–7″ zu „+7″ wird.
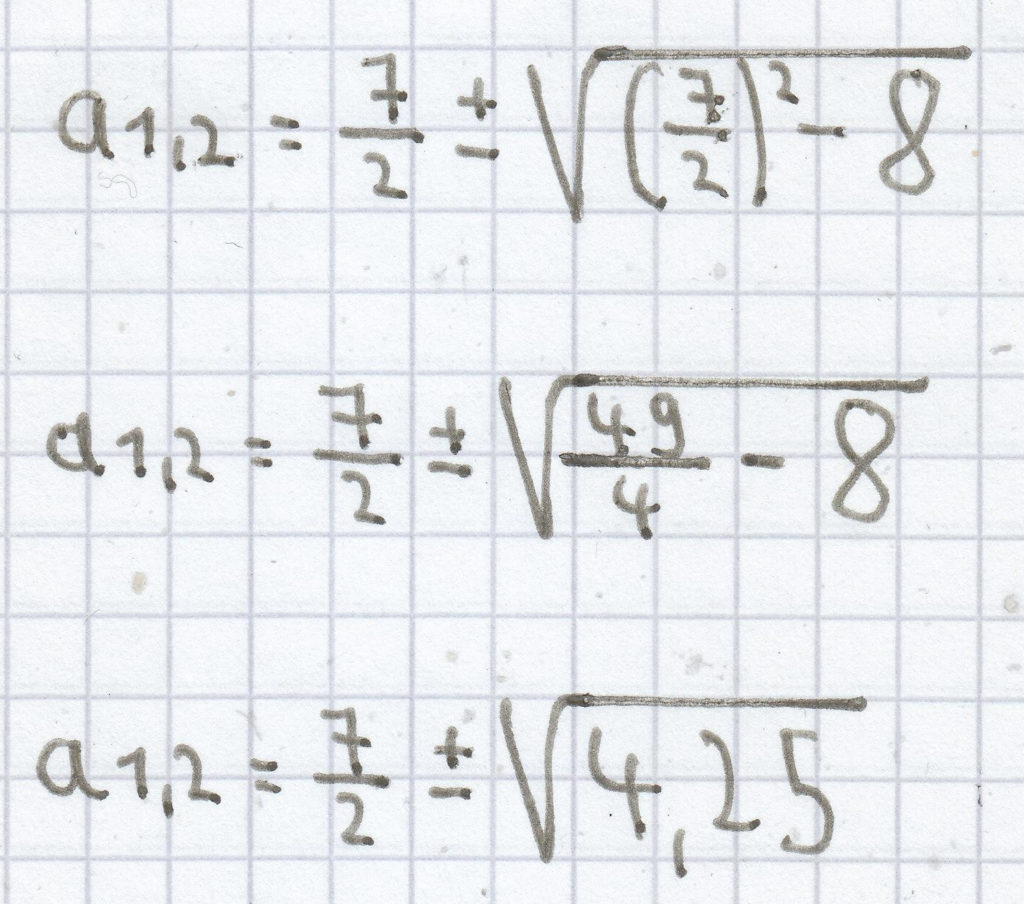
a1,2 = 3,5 ± 2,06
a1 = 3,5 – 2,06 = 1,44
a2 = 3,5 + 2,06 = 5,56

2. Mathematik-Nachhilfe-Aufgabe: Zuerst die Diskriminante ermitteln, darauf die Anzahl der Lösungen, zuletzt die genauen Ergebnisse bestimmen.
a) x² – 17x + 70 = 0
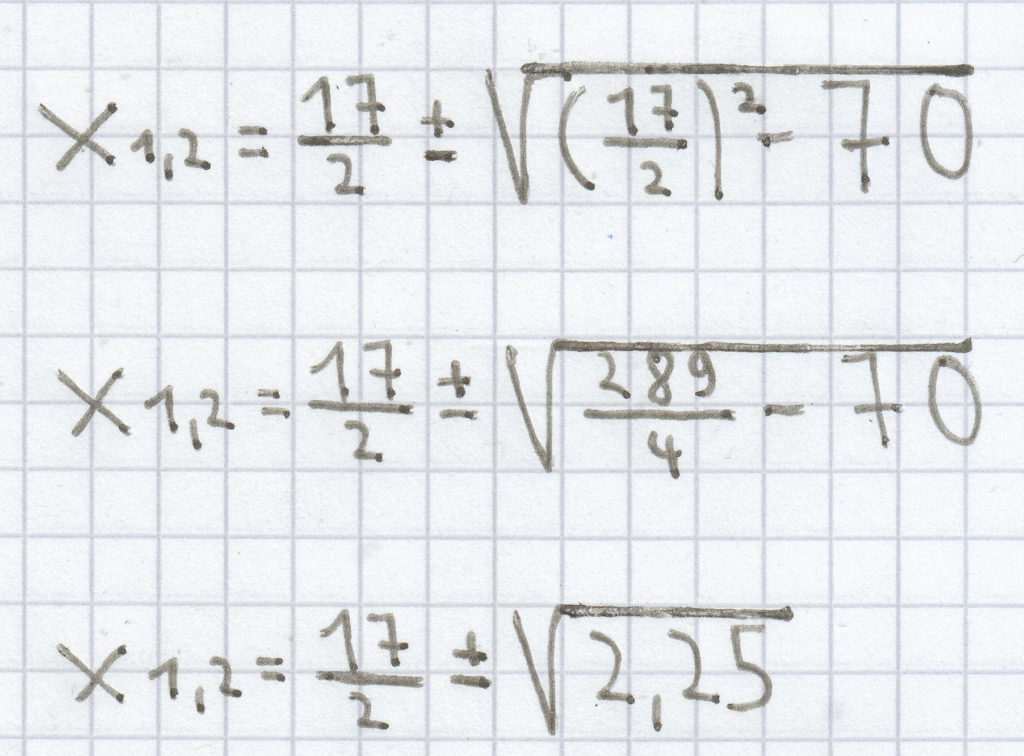
Da hier die Diskriminante > 0 ist, hat die quadratische Gleichung zwei Lösungen.
x1,2 = 8,5 ± 1,5
x1 = 8,5 – 1,5 = 7
x2 = 8,5 + 1,5 = 10
L = {7; 10}
b) x² – 1,2x – 0,64 = 0
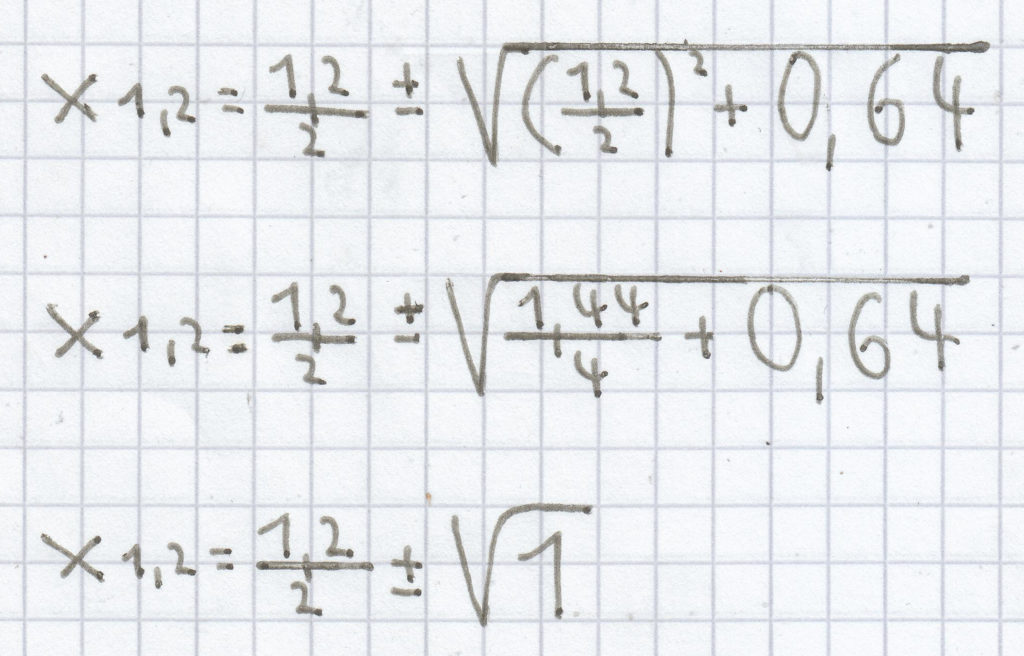
Da hier wiederum die Diskriminante > 0 ist, hat die quadratische Gleichung zwei Lösungen.
x1,2 = 0,6 ± 1
x1 = 0,6 – 1 = –0,4
x2 = 0,6 + 1 = 1,6
L = {–0,4; 1}
c) y² – 14x + 53 = 0
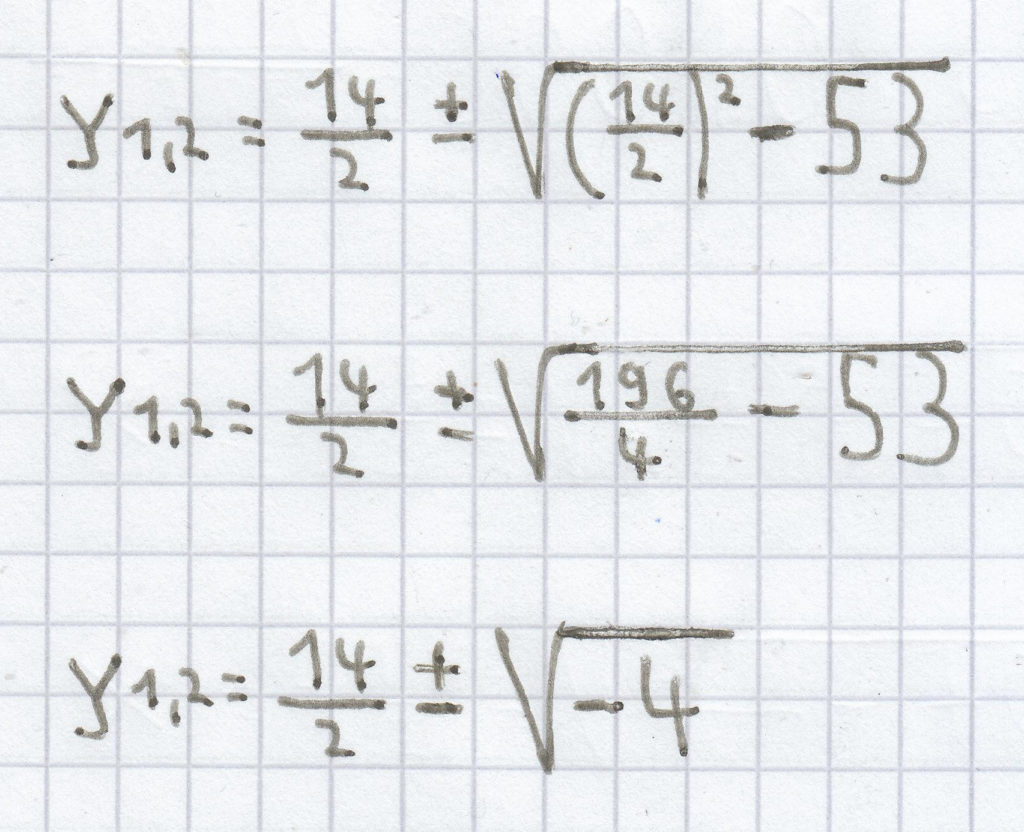
Da hier die Diskriminante < 0 ist, hat die quadratische Gleichung keine Lösung.
L = { } bzw. Ø
d) a² + 2,5a – 51 = 0
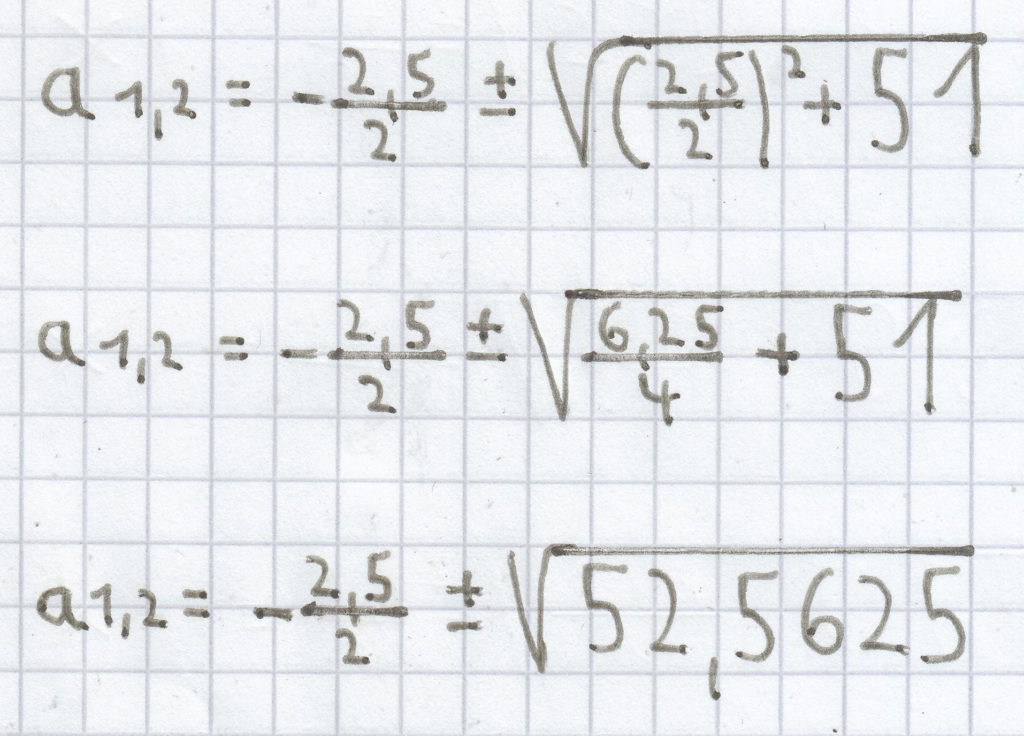
Da hier die Diskriminante > 0 ist, hat die quadratische Gleichung zwei Lösungen.
a1,2 = –1,25 ± 7,25
a1 = –1,25 – 7,25 = –8,5
a2 = –1,25 + 7,25 = 6
L = {–8,5; 6}
e) y² + 1,6x + 0,64 = 0
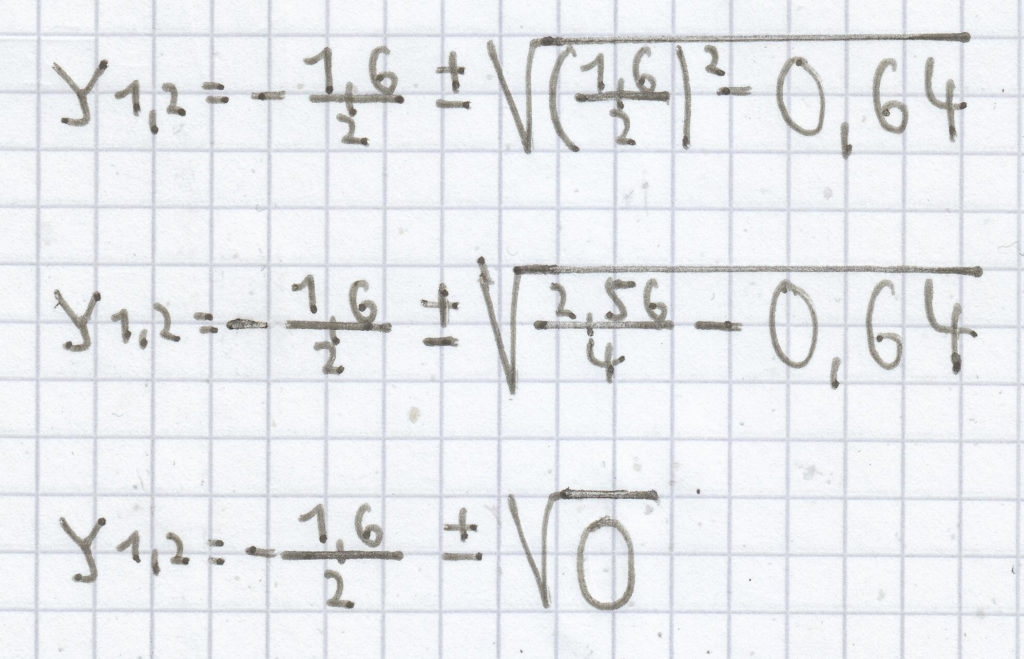
Da die Diskriminante hier null ist, hat die quadratische Gleichung nur eine Lösung.
y1,2 = –0,8 ± 0
y1,2 = –0,8
L = {–0,8}
f)
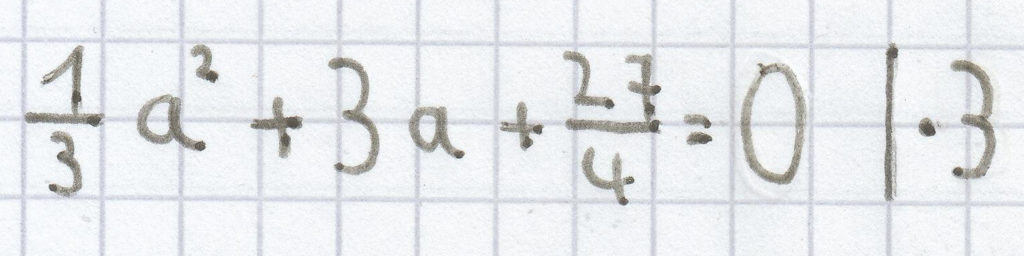
a² + 9a + 20,25 = 0
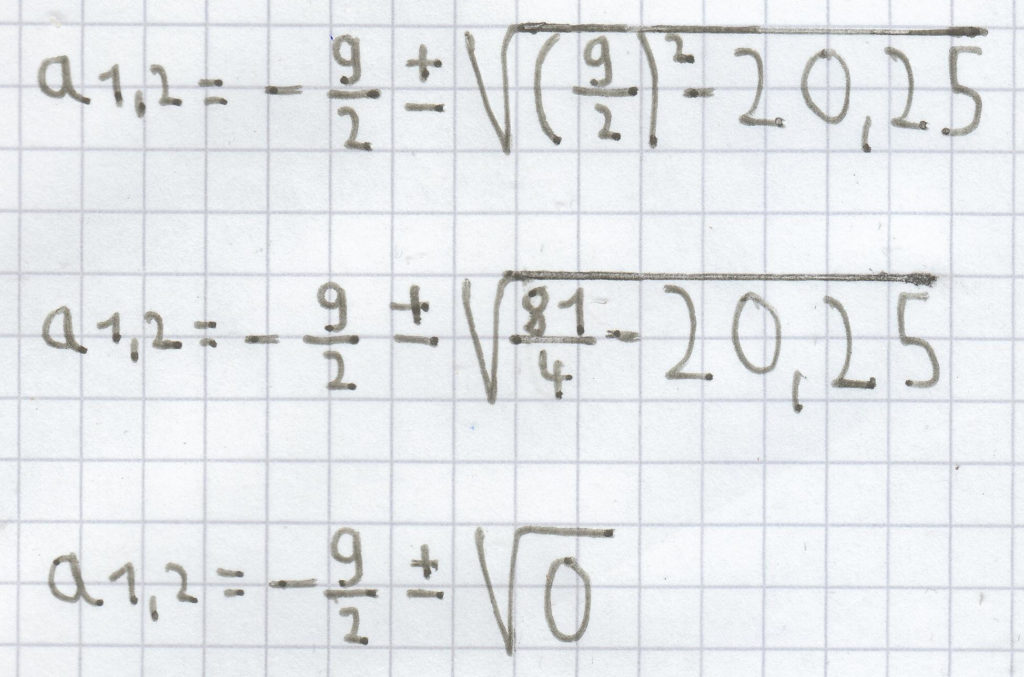
Die Diskriminante ist hier null. Daher hat die quadratische Gleichung hier nur ein Lösung.
a1,2 = –4,5 ± 0
a1,2 = –4,5
L = {–4,5}
g) 10y² – 4x + 3 = 0 | : 10
y² – 0,4x + 0,3 = 0
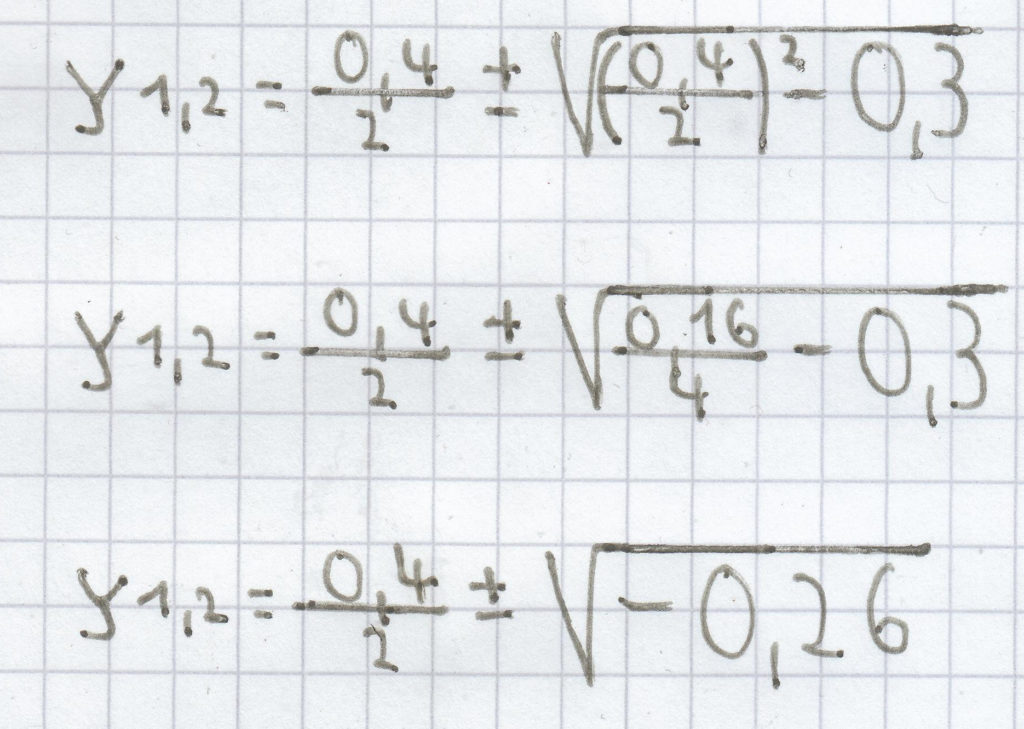
Hier ist die Diskriminante negavtiv. Daher hat die quadratische Gleichung keine Lösung.
L = { } bzw. Ø
h) x² – 2,8x + 3,61 = 0
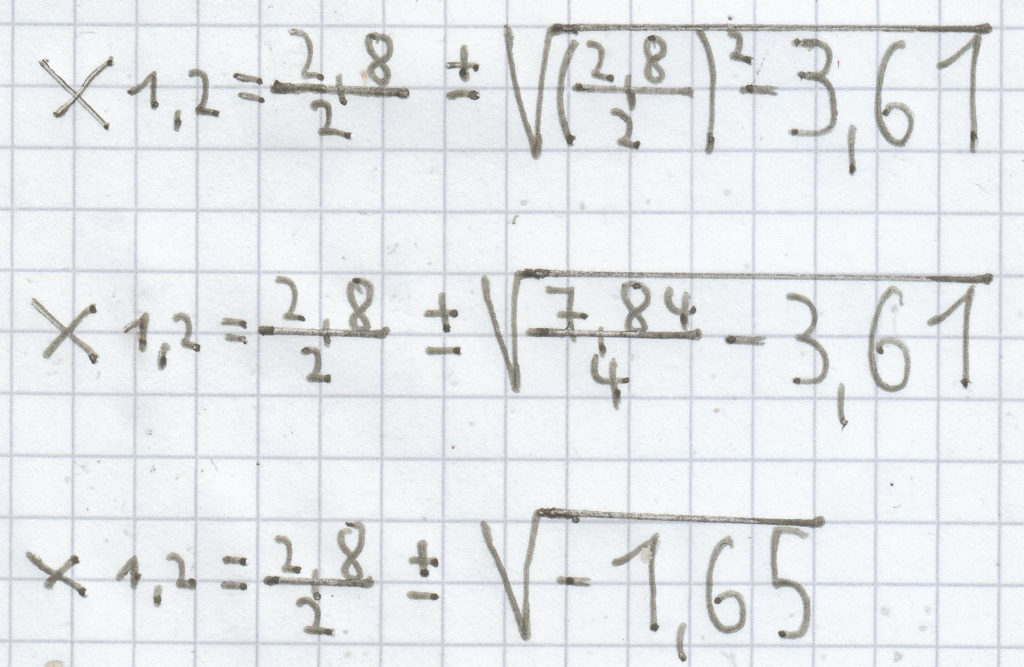
Da hier wiederum die Diskrimninate negativ ist, hat die quadratische Gleichung keine Lösung.
L = { } bzw. Ø
3. Mathe-Nachhilfe-Aufgabe: Bringe zunächst die quadratische Gleichung in die Form x² + px = 0 und bestimme dann die Lösungen.
a) x (2x + 18) = 0
2x² + 18x = 0 | : 2
x² + 9x = 0
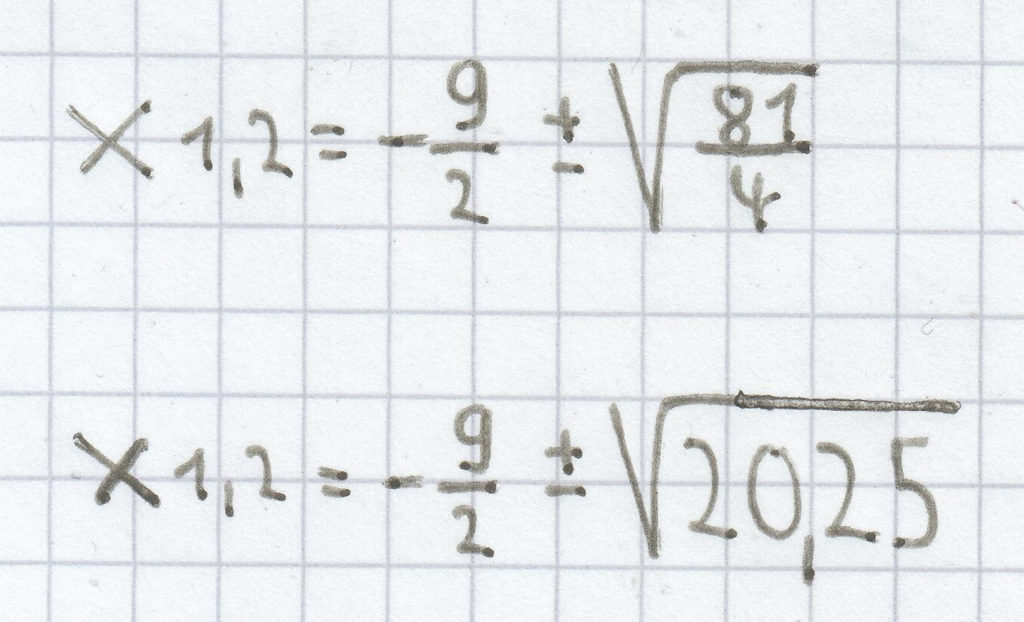
x1,2 = –4,5 ± 4,5
x1 = –4,5 – 4,5 = –9
x2 = –4,5 + 4,5 = 0
L = {–9; 0}
b) (8 + x) (4x – 6) = –48
32x² – 48 + 4x² – 6x = –48
36x² – 48 – 6x = –48 | + 48
36x² – 6x = 0 | : 36
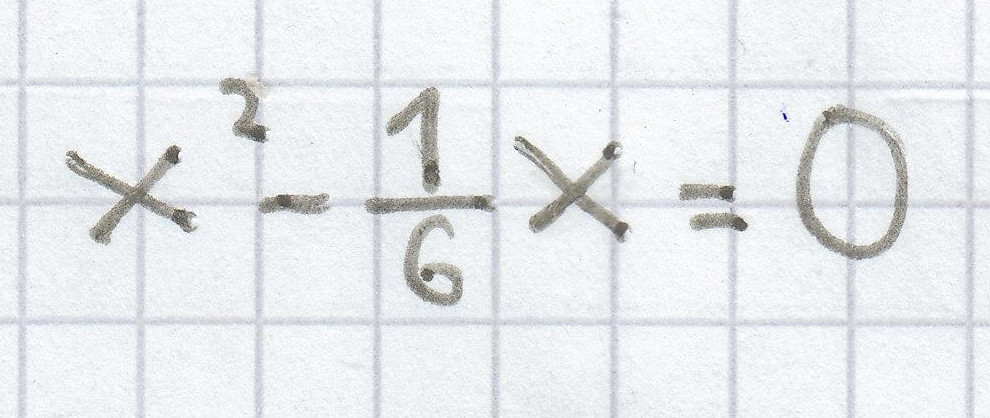
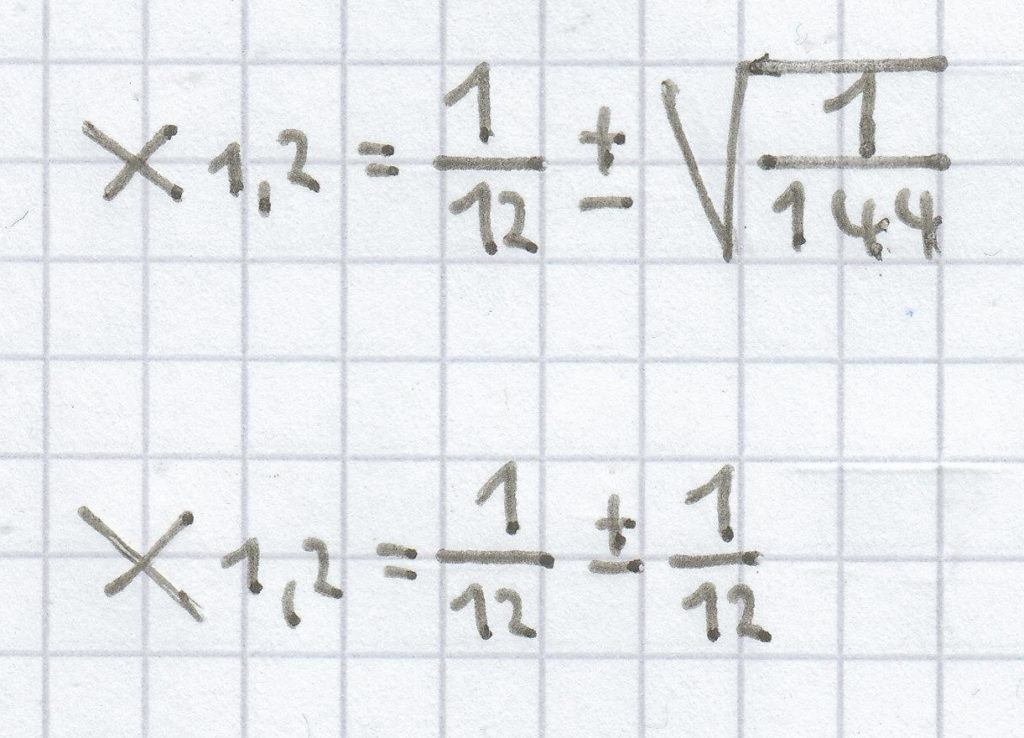
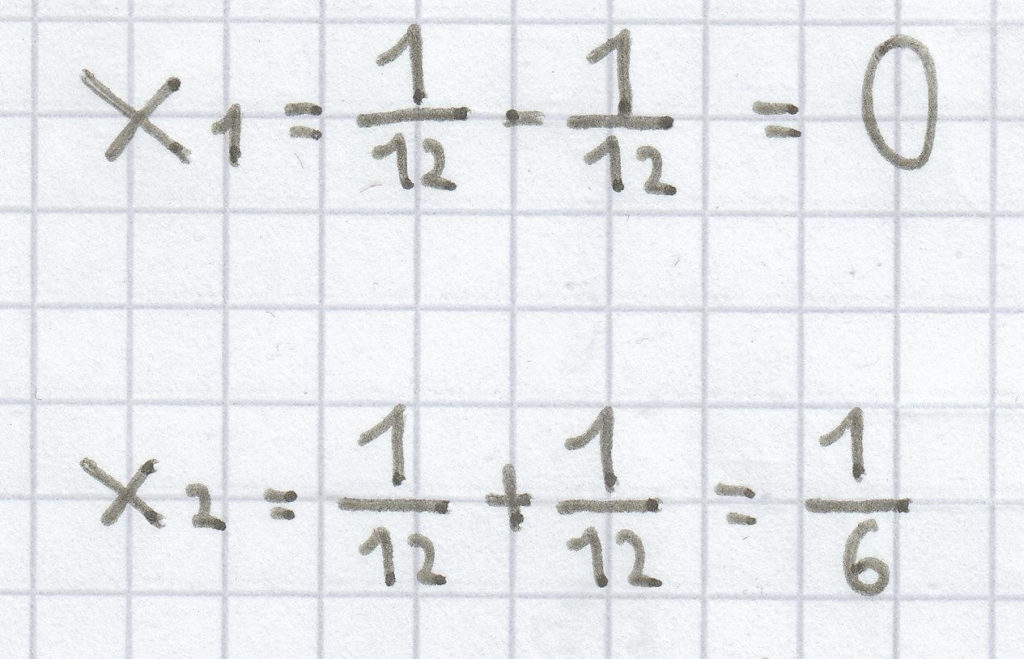
L =
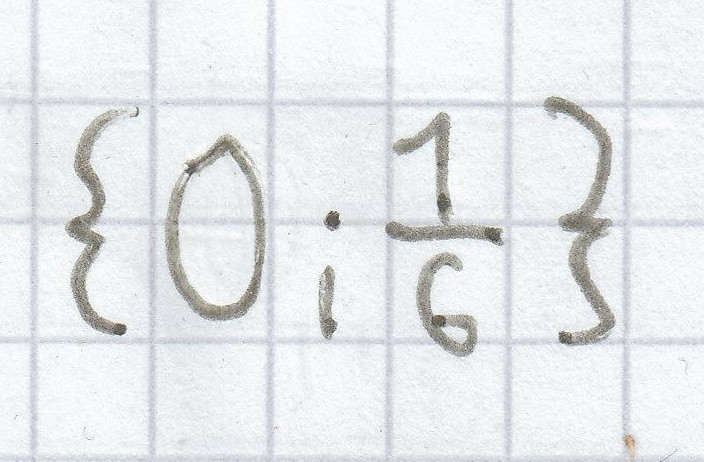
c) (y – 10) (y – 5) = 50
y² – 5y – 10y + 50 = 50
y² – 15y + 50 = 50 | – 50
y² – 15y = 0
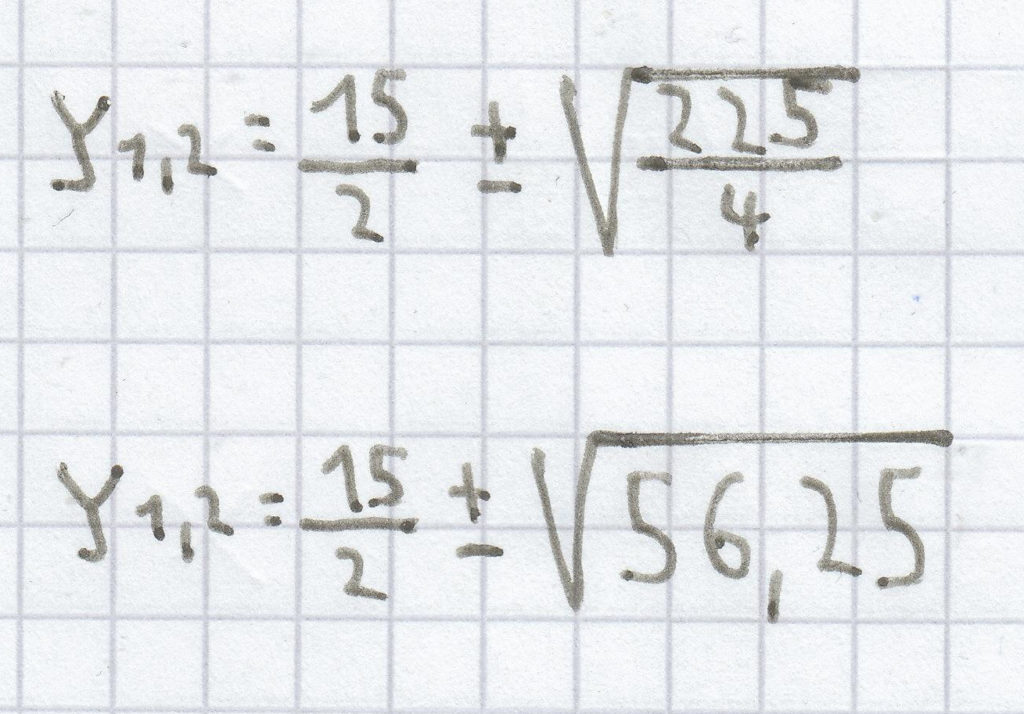
y1,2 = 7,5 ± 7,5
y1 = 7,5 – 7,5 = 0
y2 = 7,5 + 7,5 = 15
L = {0; 15}
d) (3x + 5) x + 1 = (2x + 1)²
3x² + 5x + 1 = 4x² + 4x + 1 | – 1
3x² +5x = 4x² + 4x | – 4x
3x² + x = 4x² | – 4x²
–x² + x = 0 | · (–1)
x² – x = 0
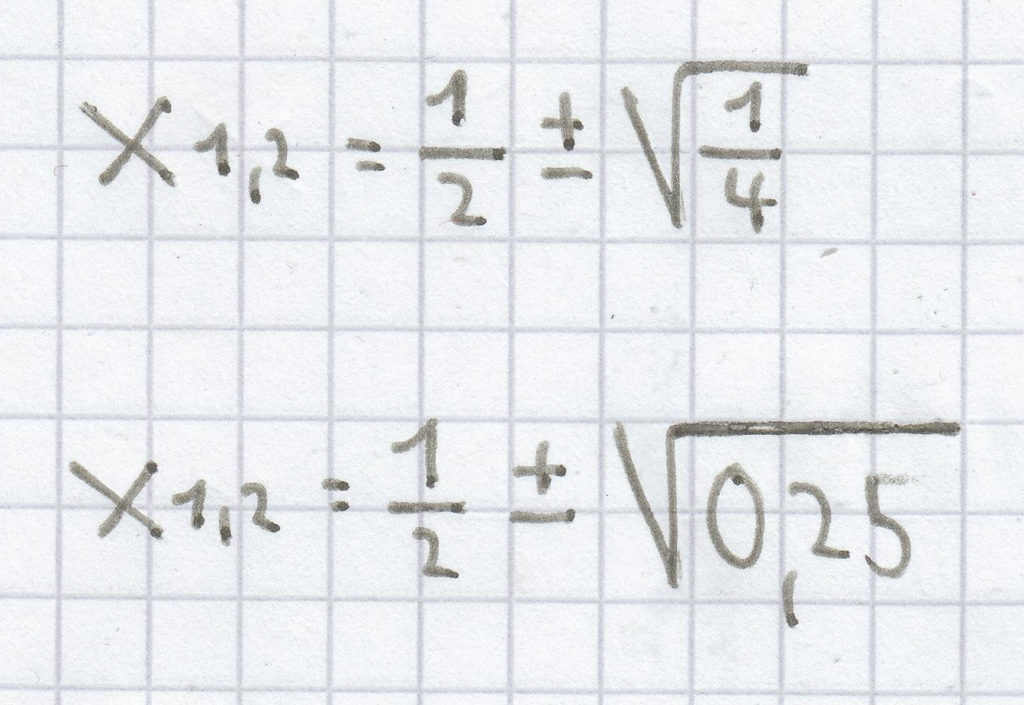
x1,2 = 0,5 ± 0,5
x1 = 0,5 – 0,5 = 0
x2 = 0,5 + 0,5 = 1
L = {0; 1}
e) (2a – 5) (5a – 2) = 10
10a² – 4a – 25a + 10 = 10
10a² – 29a +10 = 10 | – 10
10a² – 29a = 0 | : 10
a² – 2,9a = 0
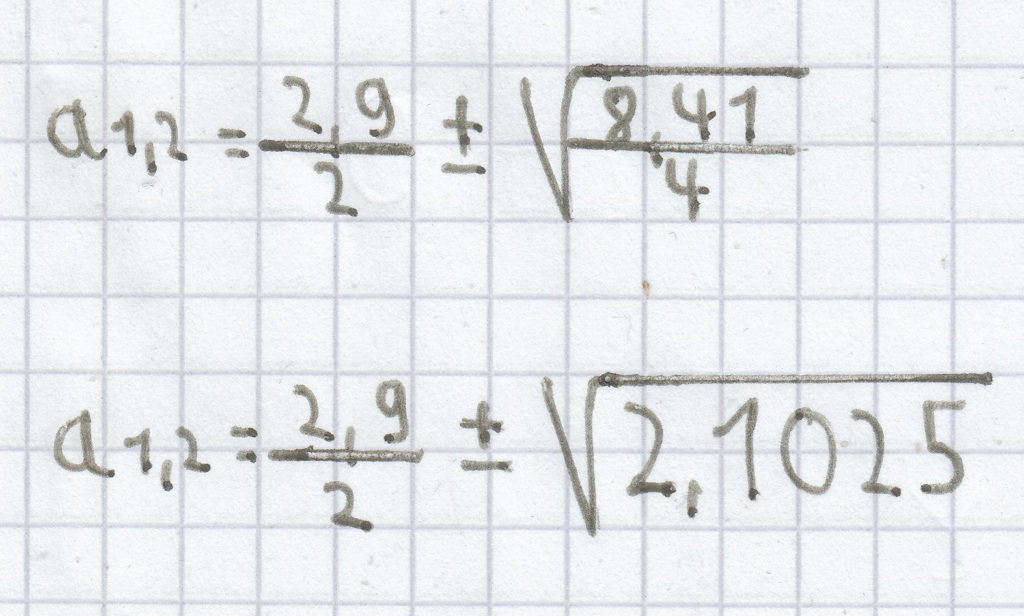
a1,2 = 1,45 ± 1,45
a1 = 1,45 – 1,54 = 0
a2 = 1,45 + 1,45 = 2,9
L = {0; 2,9}
f) 25 + 4x (2x + 1) = (5 + 3x)²
25 + 8x² + 4x = 25 + 30x + 9x² | – 25
8x² + 4x = 30x + 9x² | – 8x²
4x = 30x + x² | – 4x
0 = 26x + x²
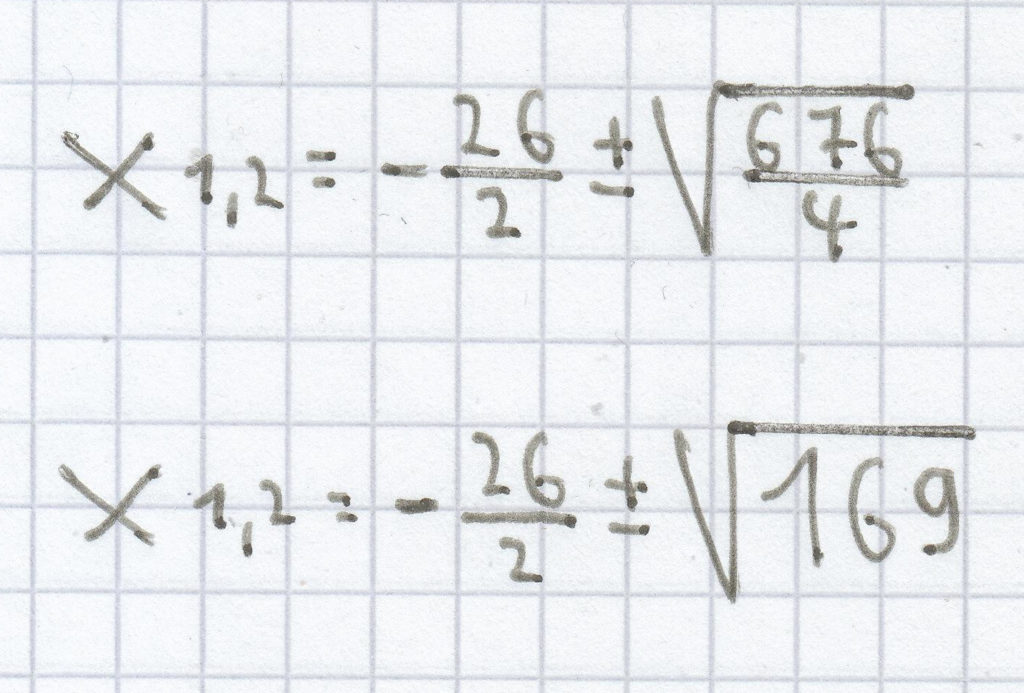
x1,2 = –13 ± 13
x1 = –13 – 13 = –26
x2 = –13 + 13 = 0
L = {–26; 0}