
Hat man gedacht: „Zum Glück habe ich das Mathe-Stoffgebiet lineare Gleichungen (und Funktionen) endlich hinter mir“, so muss man beim nächsten darauf aufbauenden sicherlich ordentlich Schlucken – quadratische Gleichungen (und Funktionen). Denn der Schwierigkeitsgrad bei diesem Stoffgebiet ist auch um einiges höher im Vergleich zu linearen Gleichungen und Funktionen. Das liegt an der höheren Potenz, dem „hoch 2″, das eine Variable bei einer quadratischen Gleichung (und Funktion) immer vorweist. Jetzt könnte aber ein mitdenkender Schüler entgegenhalten: „Da ja gegenüber linearen Gleichungen (und Funktionen) die Potenz nur um eins zunimmt, kann doch an sich der Schwierigkeitsgrad nicht enorm viel höher sein!“ Hier ist zu entgegnen: „Das stimmt auch an sich, dass diese Gleichungen (und Funktionen) für einen in Mathe nicht auf den Kopf gefallenen Schüler kein allzu großes Problem darstellen, da die Verkomplizierung zu linearen Gleichungen (und Funktionen) sich auch in Grenzen hält.“

Hat man daher das Mathematik-Stoffgebiet lineare Gleichungen (und Funktionen) gut verstanden, so wird das auch ganz sicher mit linearen Gleichungen (und Funktionen) der Fall sein. Da man jede quadratische Gleichung unabhängig von ihrer graphischen Darstellung als Funktion betrachten kann, kann man zuerst einmal (wie bei linearen Gleichungen natürlich ebenso ;-)) quadratische Funktionen AUSKLAMMERN und sich voll und ganz dem Lösen dieser Gleichungen widmen. Denn quadratische Gleichungen sind in Mathematik auch gerade in der Oberstufe stets omnipräsent, sprich allgegenwärtig, und sollten immer schnellstmöglich und natürlich fehlerfrei gelöst werden können. Das Lösen einer quadratischen Gleichung sollte hierbei stets abhängig sein, es sei denn es ist explizit vorgegeben (wie beispielsweise „Löse die Gleichung mittels quadratischen Ergänzens oder der pq-Formel“), von der jeweiligen vorliegenden Form der quadratischen Gleichung. Je nach Form bietet sich nämlich normalerweise immer ein bestimmtes Lösungsverfahren an, das am schnellsten das gewünschte Ergebnis liefert.
Aufgaben zum Mathematik-Stoffgebiet Quadratische Gleichungen
1. Mathematik-Nachhilfe-Aufgabe: Bestimme jeweils die Lösungsmenge der reinquadratischen Gleichungen.
a)
x² = 16;
x² – 25 = 0;
x² – 2,25 = 0
b)
0,3x² = 0,012;
0,25x² = 0;
4y² – 9 = 0
c) 0,25a² = 25;
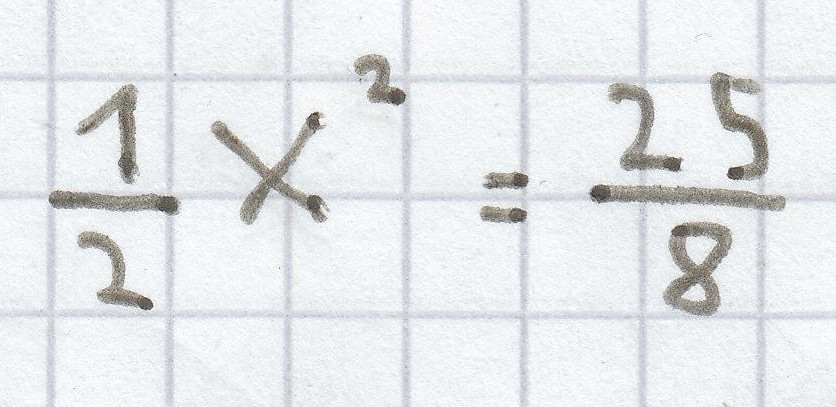
;
4x² + 1 = 0
d)

Reinquadratische Gleichung
;
0,24y² – 6 = 0;
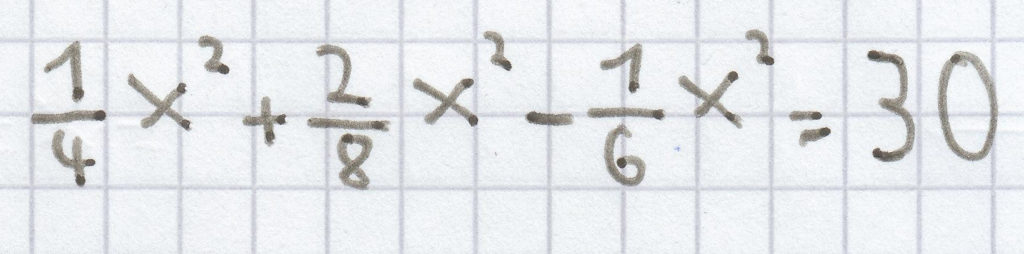
e)
(x – 4)² + (x + 4)² = 34;
–3(x + 8) = (x – 8) · (x + 5);
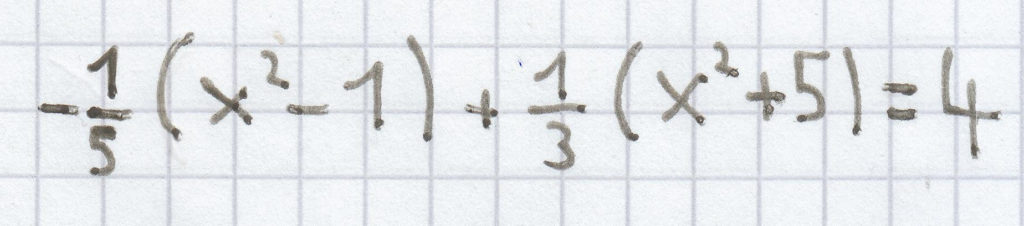
2. Mathe-Nachhilfe-Aufgabe: Gib zu folgenden Lösungsmengen jeweils eine reinquadratische Gleichung an.
a) {–5; 5};
b) {0};
c)

;
d)

;
e) { };
g) {–0,5; 0,5};
h)
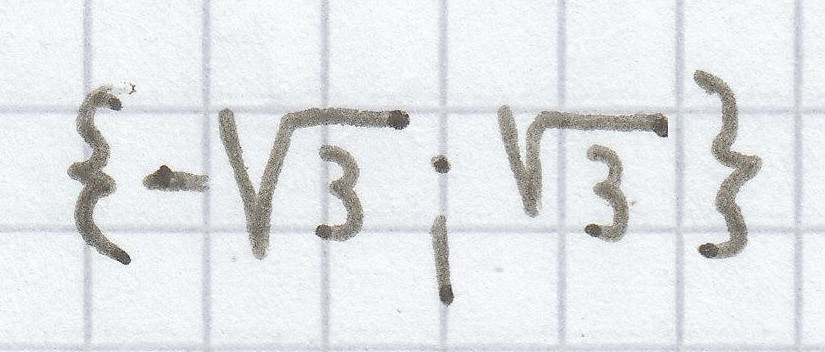
;
i)
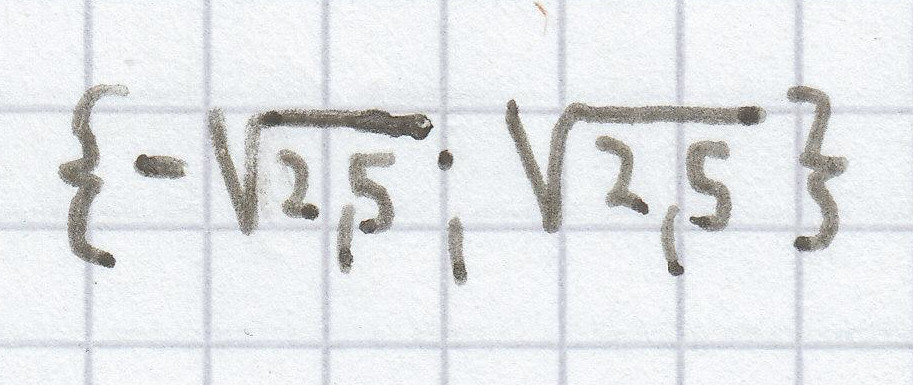
3. Mathe-Nachhilfe-Aufgabe: Bestimme bei folgenden quadratischen Gleichungen zunächst jeweils die Lösungsmenge und überprüfe anschließend das Ergebnis mittels Probe.
a) (x – 4)² = 1
b) (y + 2)² = 25
c) (a + 7)² = 36
d) (x + 2)² = 0
e) (z – 3)² = 16
f) (a – 5)² = –25
g) (x – 2)² = 16
h) (x + 1,2)² = 0,49
i) (x – 0,6)² = 20,25
Lösungen zu dem Mathematik-Stoffgebiet Quadratische Gleichungen
1. Mathe-Nachhilfe-Aufgabe: Ermittle die Lösungsmenge der reinquadratischen Gleichung.
a)
x² = 16 | √
Hier kann man direkt die Wurzel ziehen, um das Ergebnis der quadratischen Gleichung zu ermitteln.
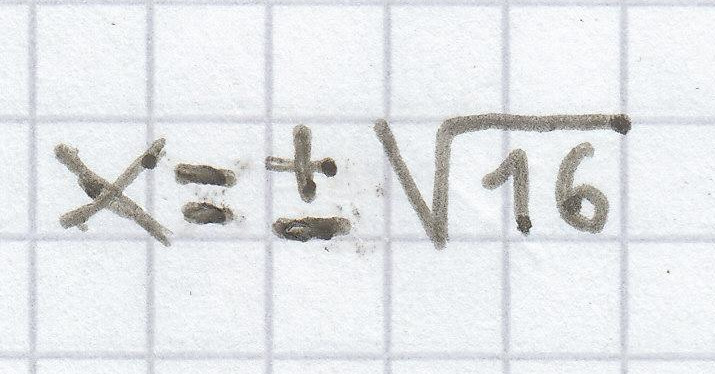
x = ± 4
L = {–4; 4}
a)
x² – 25 = 0 | + 25
Hier muss man erst die „nackte“ Zahl auf die andere Seite der Gleichung bringen, damit man das Ergebnis der quadratischen Gleichung ermitteln kann.
x² = 25 | √
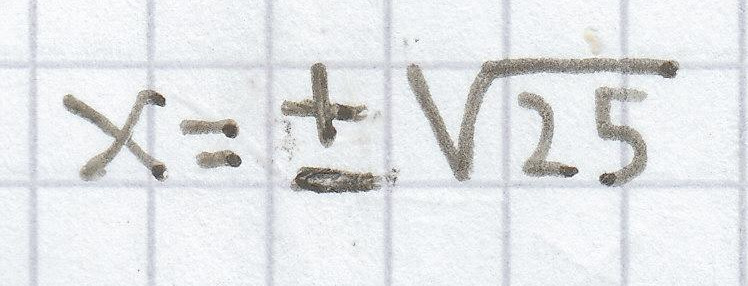
x = ± 5
L = {–5; 5}
a)
x² – 2,25 = 0 | + 2,25
Hier muss man ebenso erst die „nackte“ Zahl auf die andere Seite der Gleichung bringen. Darauf kann man die Wurzel ziehen und das Ergebnis der quadratischen Gleichung offen legen.
x² = 2,25 | √
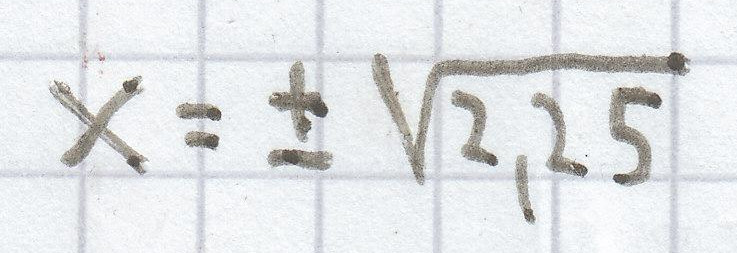
Lösung quadratische Gleichung
x = ± 1,5
L = {–1,5; 1,5}
b)
0,3x² = 0,012 | : 0,3 <=>
Hier muss man zuerst den Faktor vor der Potenz eliminieren. Darauf kann man das Ergebnis der quadratischen Gleichung ermitteln.
x² = 0,04 | √

x = ± 0,2
L = {–0,2; 0,2}
b)
0,25x² = 0 | : 0,25 <=>
Bei dieser quadratischen Gleichung muss man wiederum erst den Faktor vor der Potenz eliminieren, um das Ergebnis der Gleichung ermitteln zu können.
x² = 0 | √
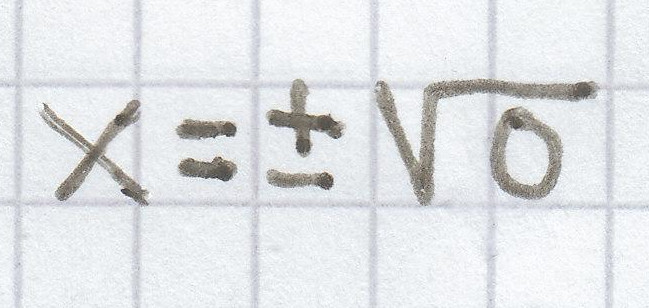
x = 0
L = {0}
b)
4y² – 9 = 0 | + 9 <=>
Hier muss man zuerst die „nackte“ Zahl auf die andere Seite der Gleichung bringen, darauf den Faktor vor der Potenz entfernen. Darauf kann man die Wurzel ziehen und die Lösung der quadratischen Gleichung ermitteln.
4y² = 9 | : 4 <=>
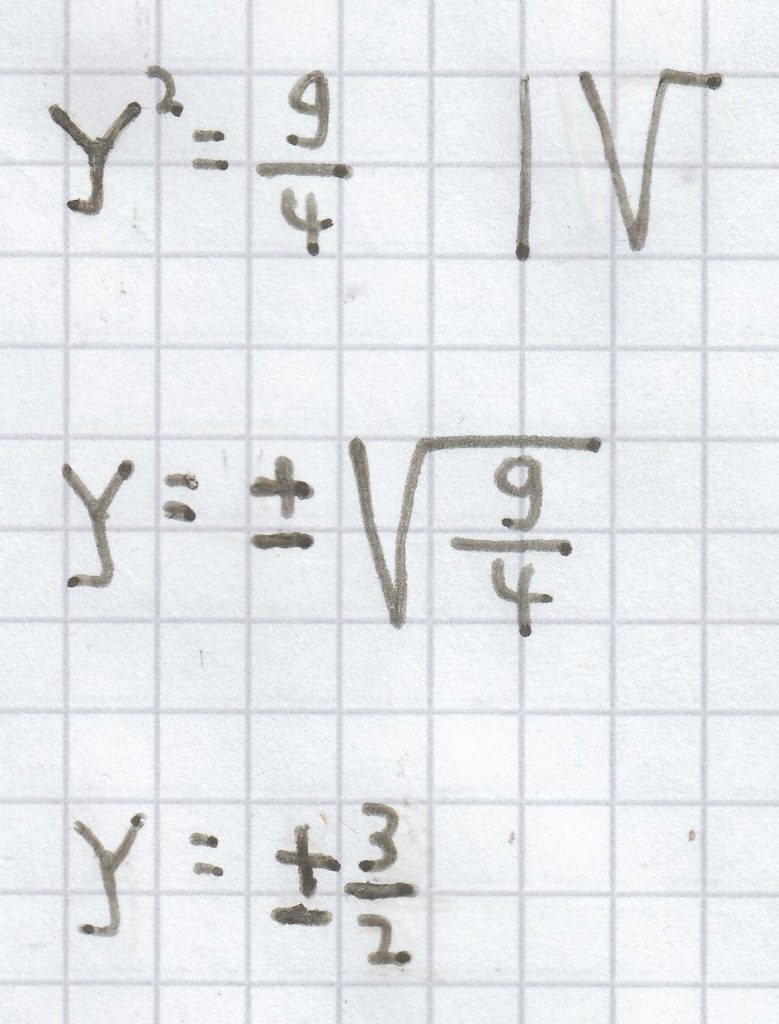
L =
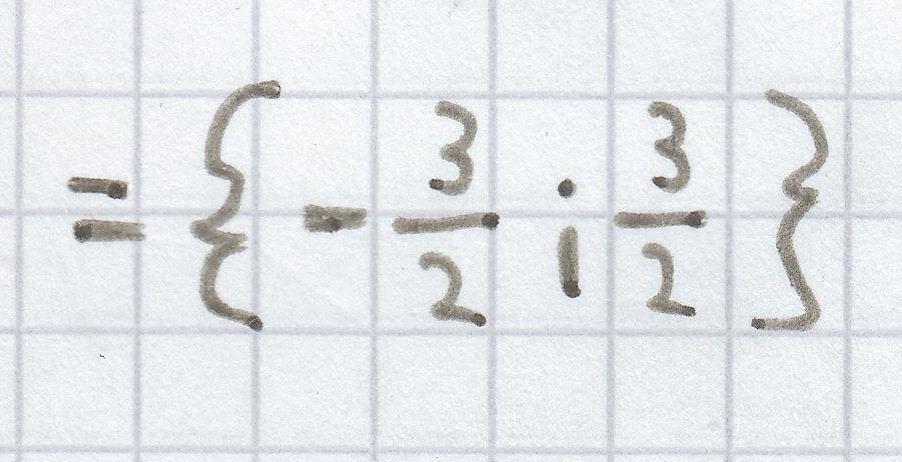
c)
0,25a² = 25 | : 0,25 <=>
Hier muss man wiederum zuerst die „nackte“ Zahl vor der Potenz eliminieren. Darauf kann man die Wurzel ziehen und die Lösung der quadratischen Gleichung ermitteln.
a² = 100 | √
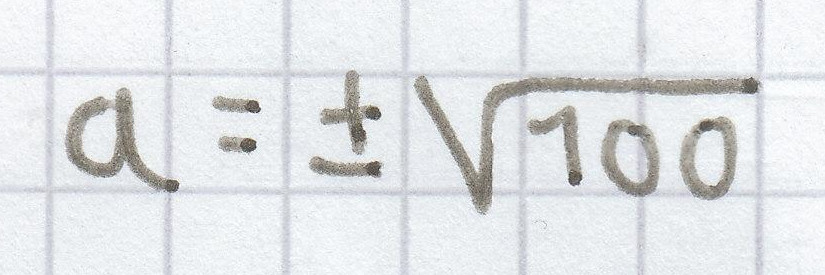
a = ± 10
L = {–10; 10}
c)
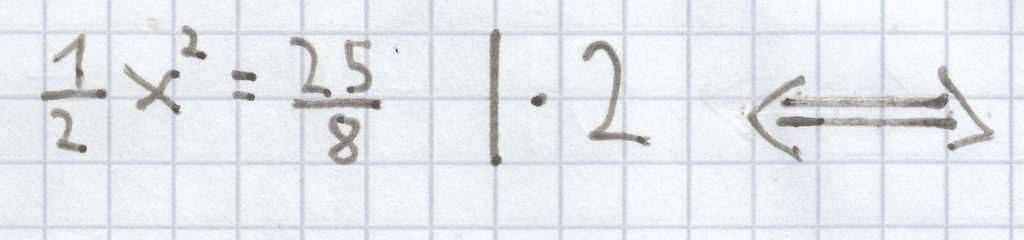
Hier gilt wieder das Gleiche, dass man zuerst den Faktor vor der Potenz entfernen muss. Darauf kann man nach dem Ziehen der Wurzel sofort die Lösung der quadratischen Gleichung bestimmen.
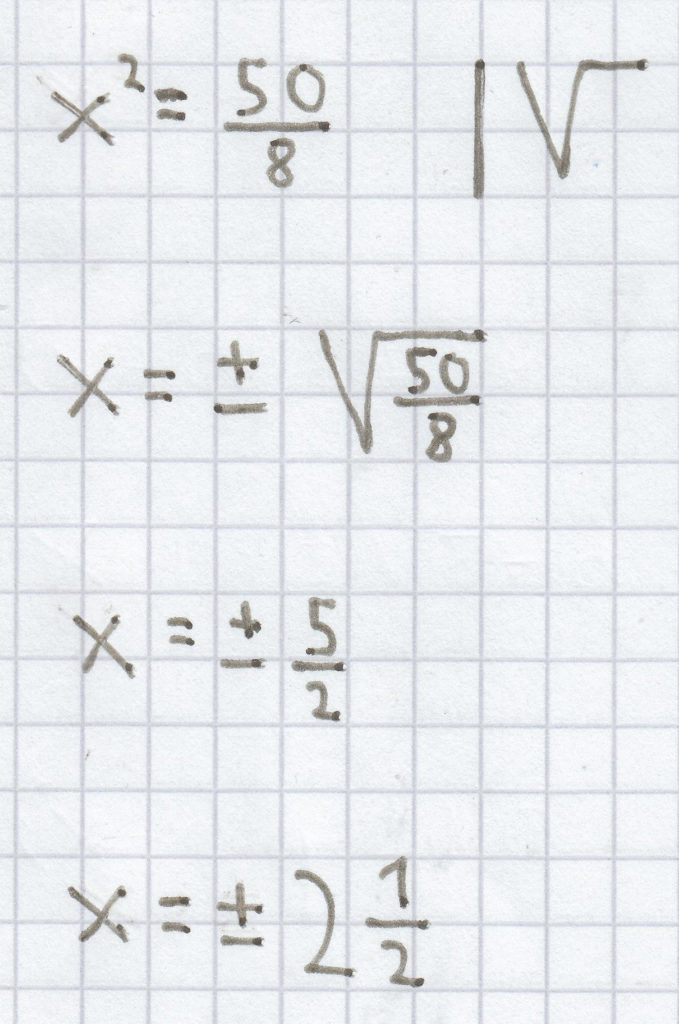
L =
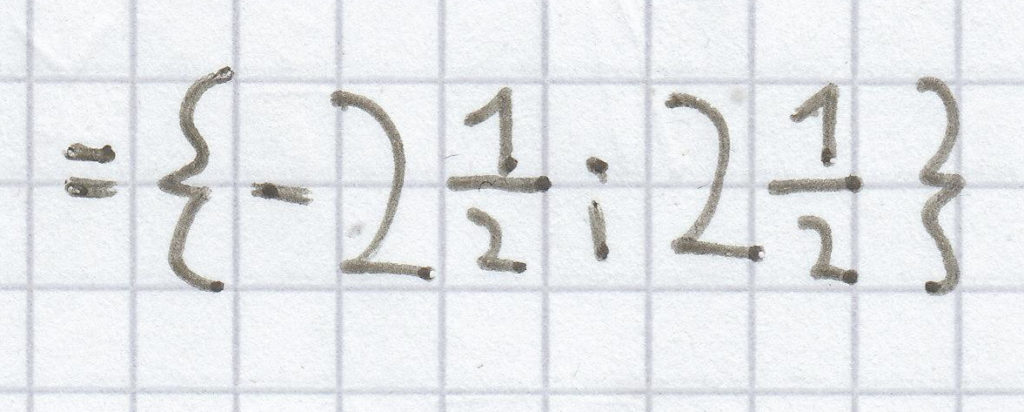
c)
4x² + 1 = 0 | – 1 <=>
Hier muss zuerst die „nackte“ Zahl auf die andere Seite der Gleichung gebracht werden. Darauf entfernt man den Faktor vor der Potenz und zieht die Wurzel. Dann erhält man die Lösung der quadratischen Gleichung.
4x² = –1 | : 4 <=>
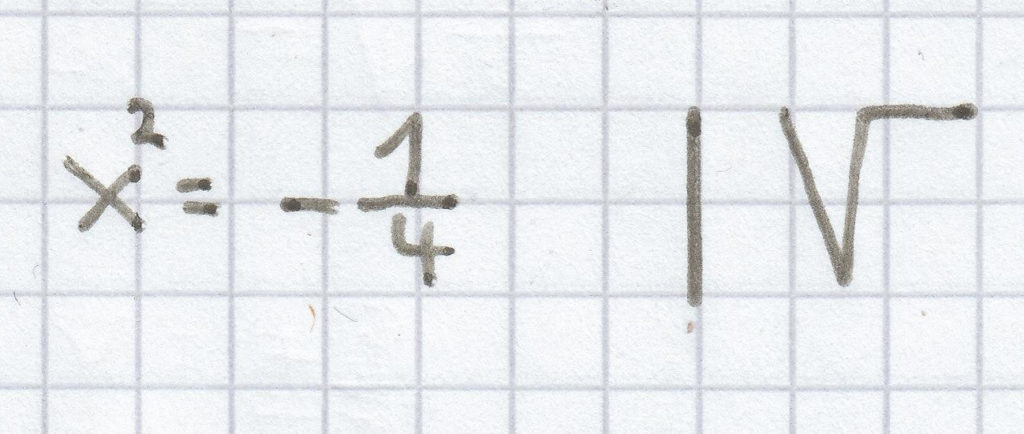
x = nicht definiert
L = { } bzw. Ø
d)
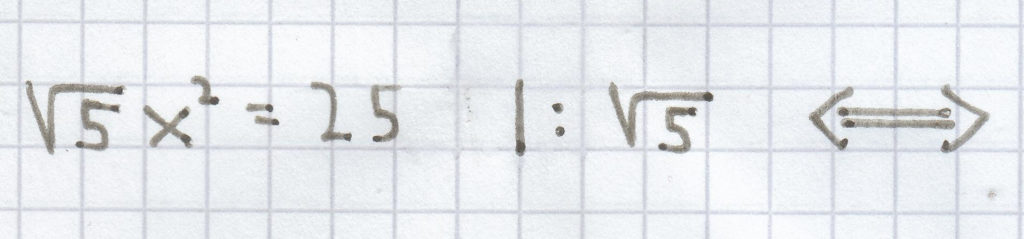
Hier gilt erneut, dass man zuerst den Faktor vor der Potenz entfernen muss. Darauf kann man nach dem Wurzelziehen die Lösung der quadratischen Gleichung ermitteln.
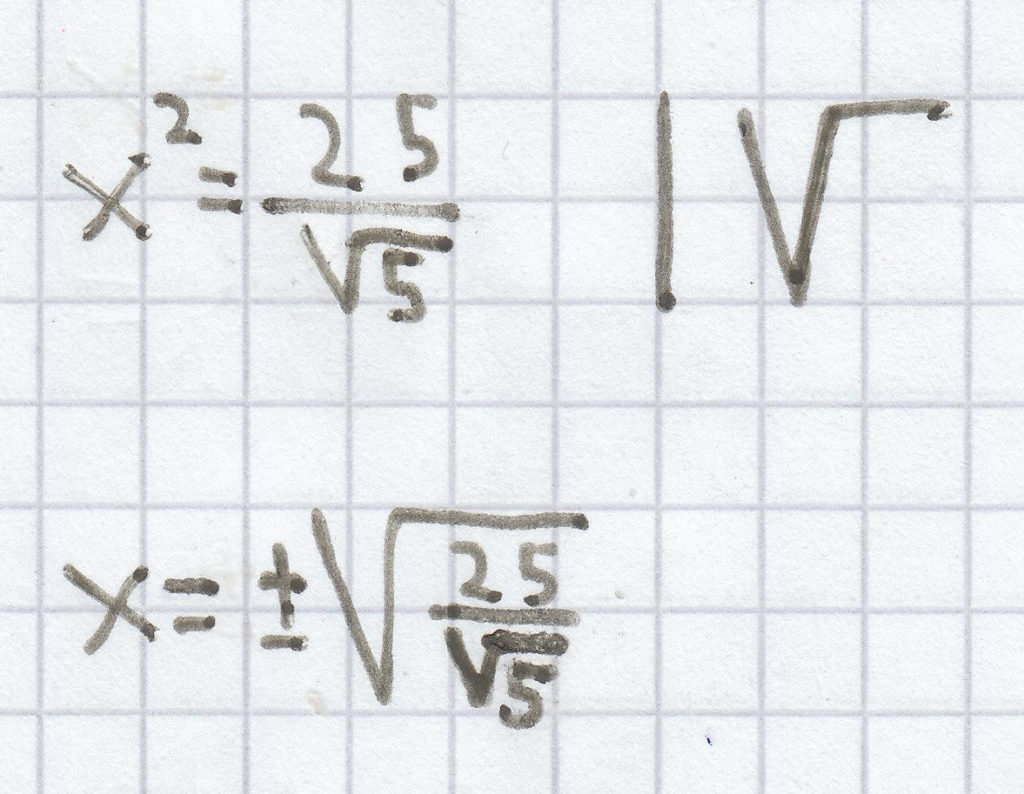
L =
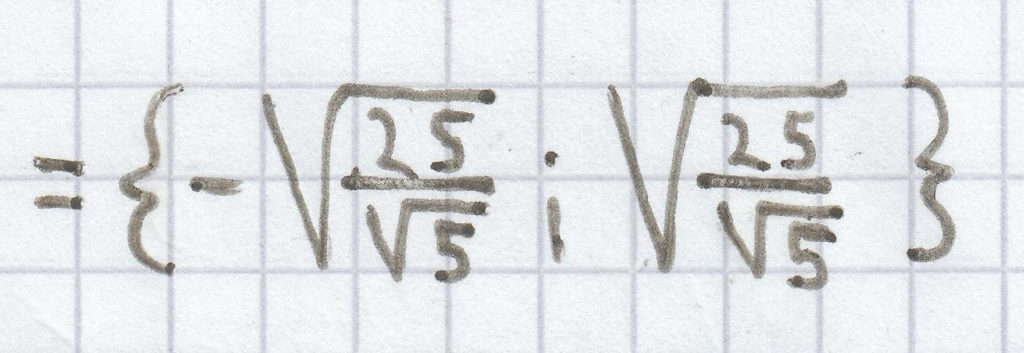
d)
0,24y² – 6 = 0 | + 6 <=>
Bei dieser quadratischen Gleichung muss man wiederum zuerst die „nackte“ Zahl auf die andere Seite der Gleichung bringen. Anschließend eliminiert man den Faktor vor der Potenz. Nach dem Wurzelziehen kann man die Lösung der Gleichung bestimmen.
y² – 6 = 0 | + 6 <=>
y² = 6 | √
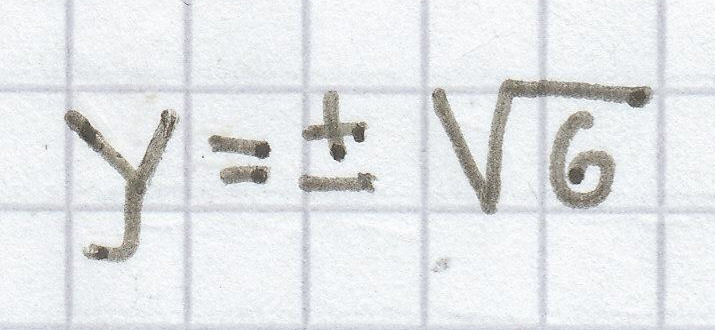
L =
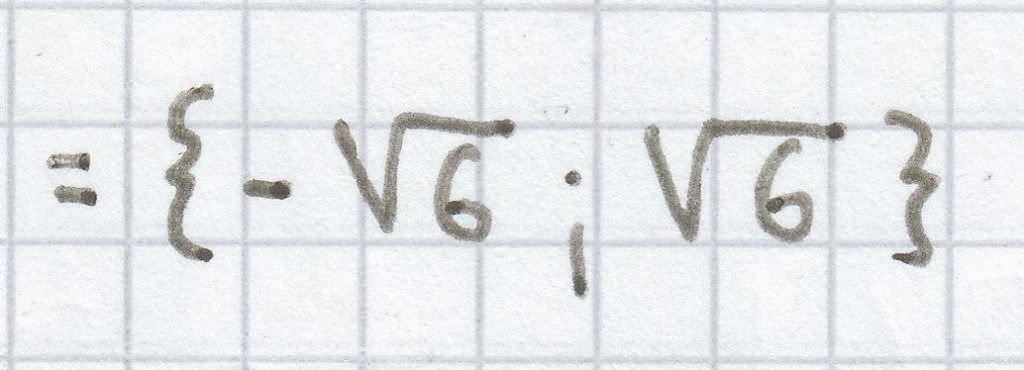
d)
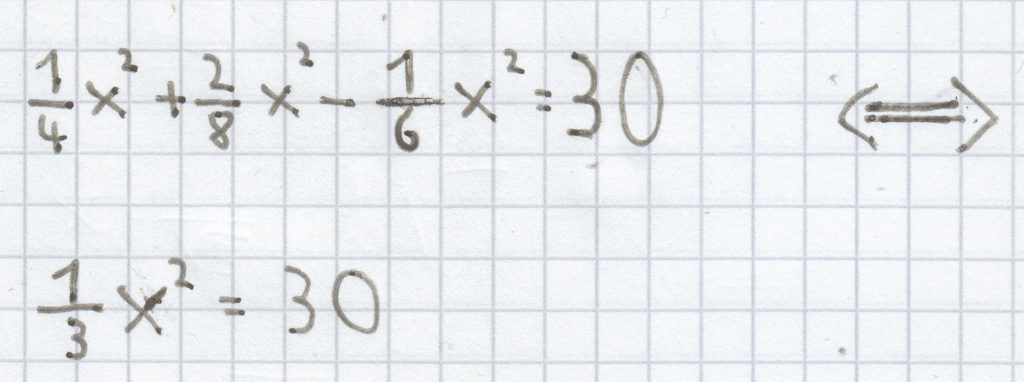
Hier muss man zuerst alle gleichen Einzelterme zusammenfassen. Darauf entfernt man die „nackte“ Zahl vor der Potenz. Nach dem Wurzelziehen kann man die Lösung der quadratischen Gleichung ermitteln.

x² = 90 | √
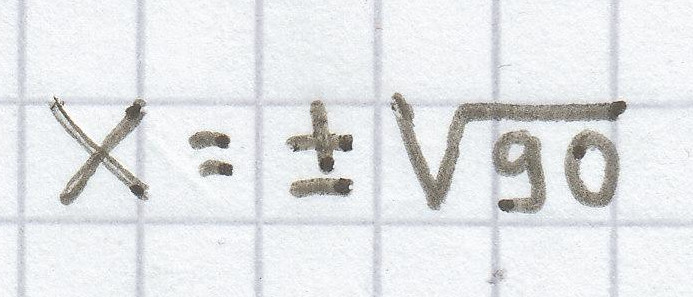
L =
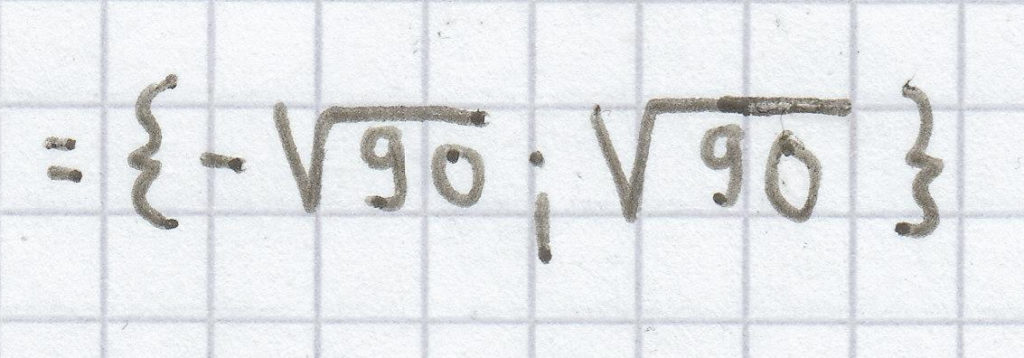
e)
(x – 4)² + (x + 4)² = 34 <=>
Hier muss man erst die beiden binomischen Formeln auflösen. Darauf die gleichen Einzelterme zusammenfassen. Danach mittels Äuqivalenzumformung die Gleichung weiter vereinfachen und dann die „nackte“ Zahl vor der Potenz eliminieren. Nach dem Ziehen der Wurzel erhält man schließlich die Lösung der quadratischen Gleichung.
(x)² – 2 · x · 4 + (4)² + (x)² + 2 · x · 4 + (4)² = 34 <=>
x² – 8x + 16 + x² + 8x + 16 = 34 <=>
2x² + 32 = 34 | – 32 <=>
2x² = 2 | : 2 <=>
x² = 1 | √
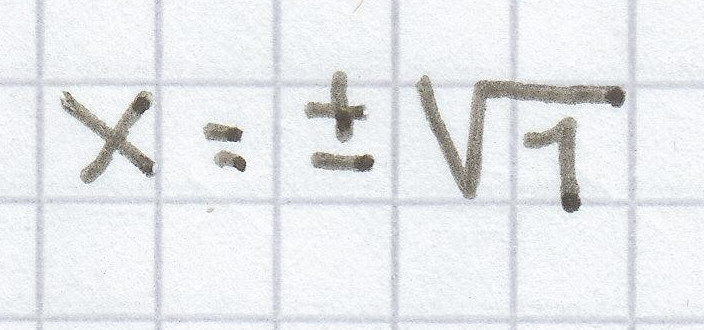
x = ± 1
L = {–1; 1}
e)
–3(x + 8) = (x – 8) · (x + 5) <=>
Zunächst muss man hier die Klammern mittels des Distributivgesetzes/Verteilungsgesetzes korrekt auflösen und darauf die gleichen Einzelterme zusammenfassen, dann mittels Äquivalenzumformungen die Gleichung weiter vereinfachen. Nach dem Wurzelziehen erhält man die Lösung der quadratischen Gleichung.
(–3) · x + (–3) · 8 = x · x + x · 5 + (–8) · x + (–8) · 5 <=>
–3x – 24 = x² + 5x – 8x – 40 <=>
–3x – 24 = x² – 3x – 40 | + 3x <=>
– 24 = x² – 40 | + 40 <=>
16 = x² | √
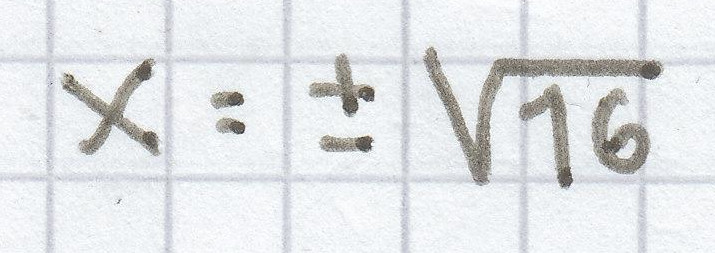
x = ± 4
L = {–4; 4}
e)
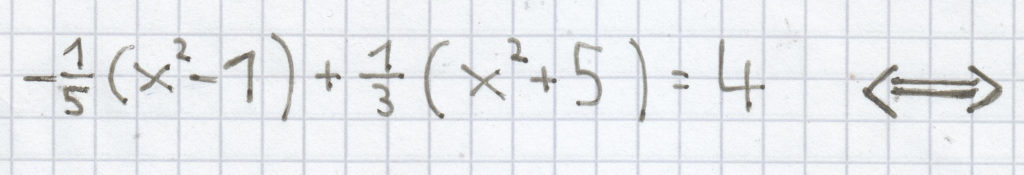
Hier muss man ebenso zunächst die Klammern korrekt auflösen, indem man das Distributivgesetz/Verteilungsgesetz anwendet. Nach dem Zusammenfassen gleicher Einzelterme muss man die Gleichung mittels Äquivalenzumformungen weiter vereinfachen. Die Lösung der quadratischen Gleichung zeigt sich nach dem Wurzelziehen.
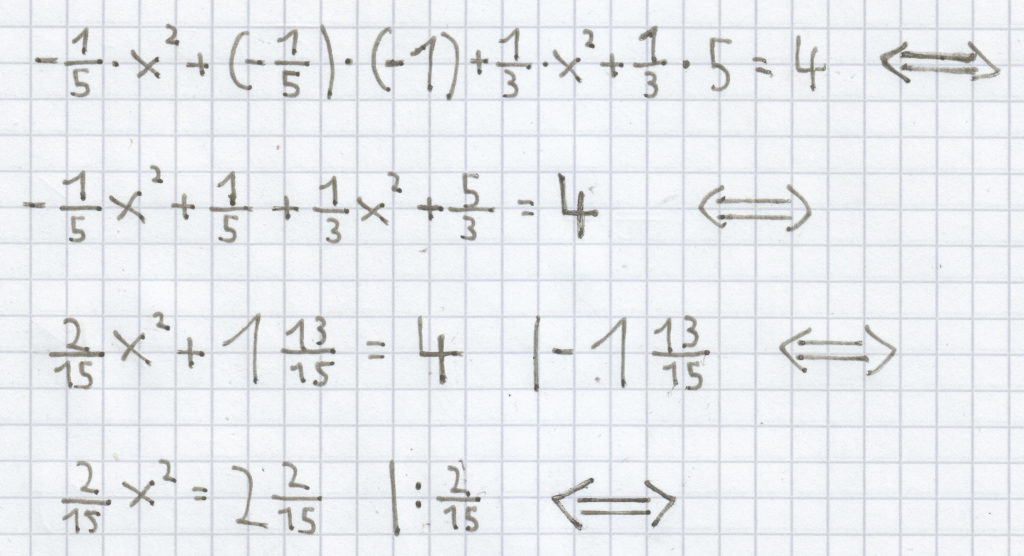
x² = 16 | √
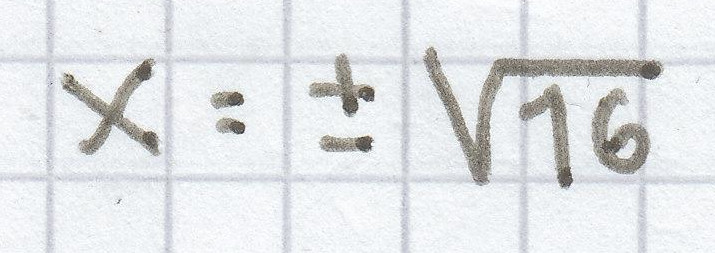
x = ± 4

2. Mathematik-Nachhilfe-Aufgabe: Wie lautet die reinquadratische Gleichung zu der angegebenen Lösungsmenge?
a) {–5; 5}
Die einfachste reinquadratische Gleichung lautet hier: x² = 25
b) {0}
Hier ist die einfachste reinquadratische Gleichung: x² = 0
c)

Hier ist die einfachste reinquadratische Gleichung:
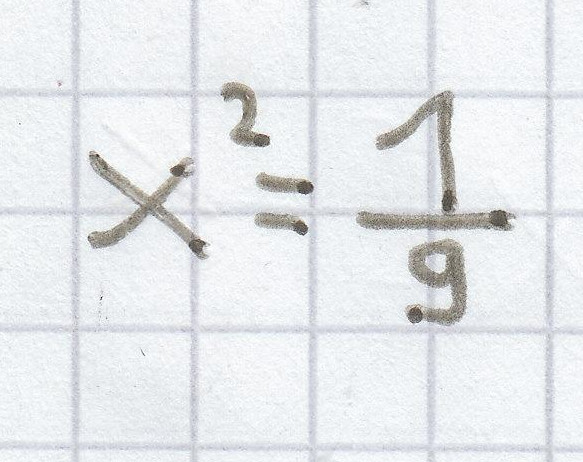
d)

Die einfachste reinquadratische Gleichung ist hier:
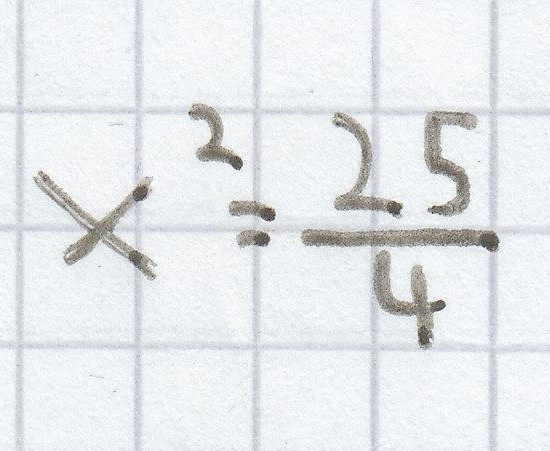
e) { }
Hier muss man einfach eine reinquadratische Gleichung wählen, die wie folgt aussieht: x² = –5. Man muss nur darauf achten, dass ein eine negative Wurzel entsteht, da dann die quadratische Gleichung keine Lösung vorweist.
g) {–0,5; 0,5}
Hier ist die einfachste reinquadratische Gleicung: x² = 0,25
h)
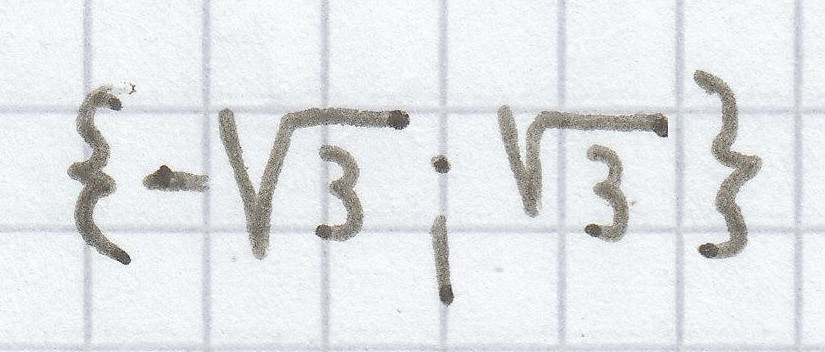
Die einfachste reinquadratische Gleichung ist hier: x² = 3
i)
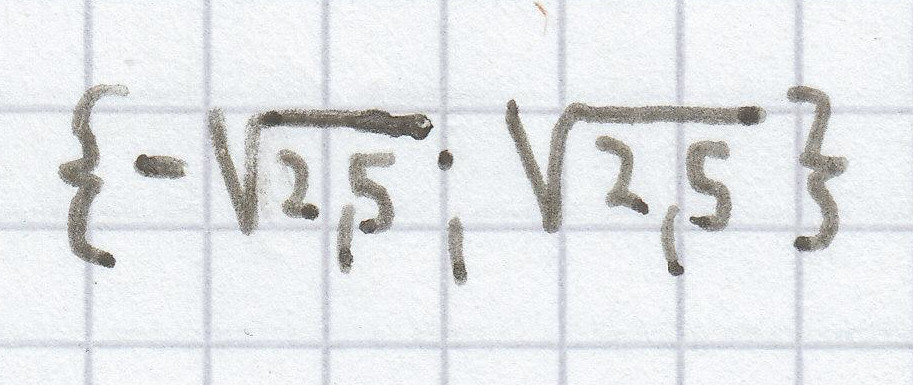
Hier ist die einfachste reinquadratische Gleichung: x² = 2,5
3 Mathe-Nachhilfe-Aufgabe: Ermittle zunächst bei den quadratischen Gleichungen die Lösungsmenge und überprüfe mittels Probe das Ergebnis.
a) (x – 4)² = 1 | √

x = ± 1 + 4
x1 = – 1 + 4 = 3; x2 = 1 + 4 = 5
L = {3; 5}
Probe:
(3 – 4)² = 1 (5 – 4)² = 1
(–1)² = 1 (1)² = 1
1 = 1 1 = 1
Die Probe bestätigt die Richtigkeit der Lösung.
b)
(y + 2)² = 25 | √
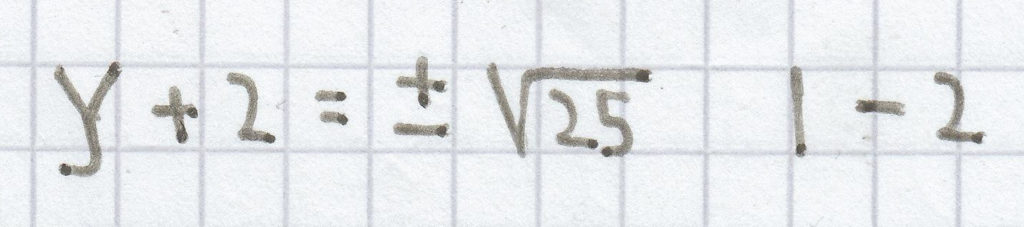
y = ± 5 – 2
y1 = –5 – 2 = –7; y2 = 5 – 2 = 3
L = {–7; 3}
Probe:
(–7 + 2)² = 25 (3 + 2)² = 25
(–5)² = 25 (5)² = 25
25 = 25 25 = 25
Die Probe legt offen, dass die Lösung korrekt ist.
c)
(a + 7)² = 36 | √
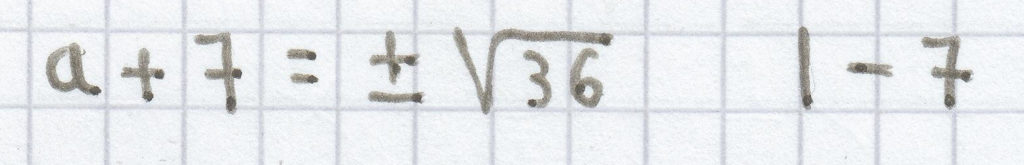
y = ± 6 – 7
y1 = –6 – 7 = –13; y2 = 6 – 7 = –1
L = {–13; –1}
Probe:
(–13 + 7)² = 36 ( –1 + 7)² = 36
(–6)² = 36 (6)² = 36
36 = 36 36 = 36
Auch hier bestätigt die Probe die Richtigkeit der Lösung.
d)
(x + 2)² = 0 | √

x = 0 – 2
x = –2
L = {–2}
Probe:
(– 2 + 2)² = 0
(0)² = 0
0 = 0
Hier bestätigt die Probe wiederum, dass die Lösung der quadratischen Gleichung richtig ist.
e)
(z – 3)² = 16 | √
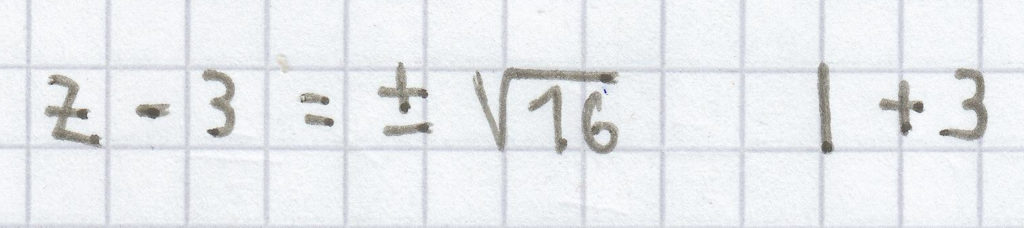
z = ± 4 + 3
z1 = –4 + 3 = –1; z2 = 4 + 3 = 7
L = {–1; 7}
Probe: (–1 – 3)² = 16 (7 – 3)² = 16
(–4)² = 16 (4)² = 16
16 = 16 16 = 16
Auch hier legt die Probe offen, dass die Lösung der quadratischen Gleichung korrekt ist.
f)
(a – 5)² = –25 | √

a = nicht definiert
L = { } bzw. Ø
Da hier eine negative Wurzel vorliegt, gibt es keine Lösung für die quadratische Gleichung.
g)
(x – 2)² = 16 | √
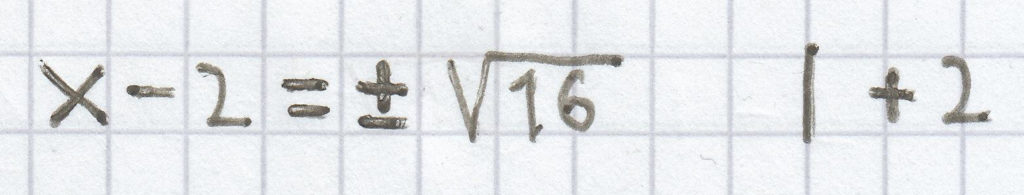
x = ± 4 + 2
x1 = –4 + 2 = –2; x2 = 4 + 2 = 6
L = {–2; 6}
Probe: (–2 – 2)² = 16 (6 – 2)² = 16
(–4)² = 16 (4)² = 16
16 = 16 16 = 16
Die Probe bestätigt, dass die Lösung der quadratischen Gleichung korrekt ist.
h)
(x + 1,2)² = 0,49 | √
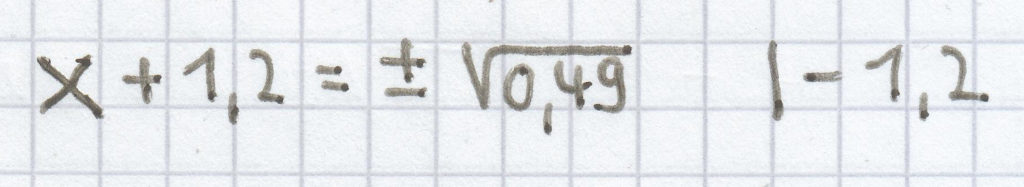
x = ± 0,7 – 1,2
x1 = –0,7 – 1,2 = –1,9; x2 = 0,7 – 1,2 = –0,5
L = {–1,9; –0,5}
Probe: (–1,9 + 1,2)² = 0,49 (–0,5 + 1,2)² = 0,49
(–0,7)² = 0,49 (0,7)² = 0,49
0,49 = 0,49 0,49 = 0,49
Die Probe zeigt auf, dass die Lösung der quadratischen Gleichung korrekt ist.
i)
(x – 0,6)² = 20,25 | √
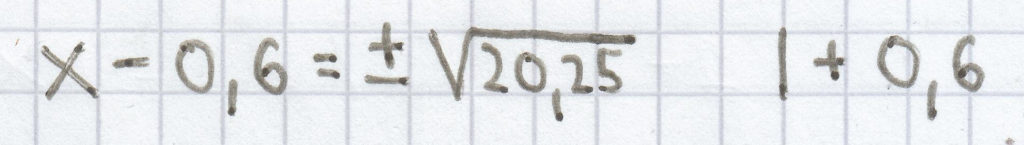
x = ± 4,5 + 0,6
x1 = –4,5 + 0,6 = –3,9; x2 = 4,5 + 0,6 = 5,1
L = {–3,9; 5,1}
Probe: (–3,9 – 0,6)² = 20,25 (5,1 – 0,6)² = 20,25
(–4,5)² = 0,49 (4,5)² = 20,25
20,25 = 0,49 20,25 = 20,25
Auch hier legt die Probe offen, dass die Lösung der quadratischen Gleichung korrekt ist.