1. Allgemeines zu Nullstellen
Bei einer Funktionsuntersuchung gibt es mit den sogenannten Nullstellen ganz besondere Punkte, die eine Funktion vorweisen kann. Bei den Nullstellen handelt es sich um Punkte, bei der die Funktion die x-Achse schneidet oder berührt.
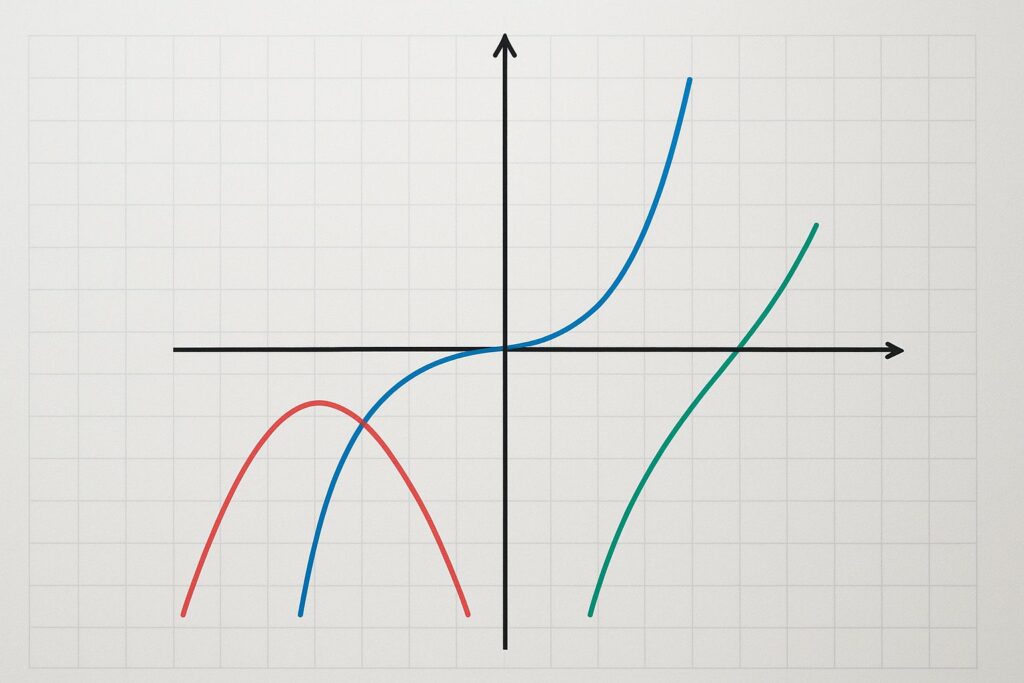
Damit man bei einer Funktion f deren Nullstellen ermitteln kann, muss man die Gleichung f(x) = 0 lösen.
Definition: Eine Zahl x1 Є Df, bei der f(x1) = 0 ist, nennt man Nullstelle der Funktion f.
2. Nullstellen ganzrationaler Funktionen
Es ist folgende Gleichung gegeben:
(x – 3) (x + 2) (x – 4) = x3 – 5x2 – 2x + 24.
Für welche x-Werte nimmt die Gleichung den Wert 0 an?
Eine ganzrationale Funktion 3. Grades (Polynomgrad 3) kann maximal drei Nullstellen vorweisen.
Daher kann die Funktion f(x) = x3 – 5x2 – 2x + 24 maximal drei Nullstellen vorweisen.
Wie man bei dem Term (x – 3) (x + 2) (x – 4) eindeutig erkennen kann, wird dieser bei folgenden x-Werten jeweils 0:
bei x = 3, bei x = – 2, bei x = 4.
Da es sich hierbei um eine Produkt, bestehend aus drei Teiltermen handeln, wird das Produkt jeweils 0, wenn einer der Faktoren, sprich Teilterme gleich null wird. Daher kann man hier die Nullstellen sofort ablesen.
Satz: Eine ganzrationale Funktion n-ten Grades (n Є ℕ) hat maximal n-Nullstellen.
2.1 Ganzrationale Funktionen 1. Grades/lineare Funktionen
Ist eine ganzrationale Funktion 1. Grades gegeben, dann erhält man deren Nullstellen folgendemaßen:
a1x + a0 = 0 | – a0
a1x = – a0 | : a1
x = $- \frac{\mathrm{a}_0}{\mathrm{a}_1}$
(für x1 ≠ 0)
Beispiel:
Es ist folgende lineare Funktion gegeben:
f(x) = 2x + 4
Hier gilt: a1 = 2 und a0 = 4.
Diese Funktion hat daher diese Nullstelle:
x = $- \frac{4}{2}$ = –2
2.2 Ganzrationale Funktionen 2. Grades/quadratische Funktionen
Liegt eine ganzrationale Funktion 2. Grades mit a2x2 + a1x + a0 vor, also eine quadratische Funktion, dann erhält man die Nullstellen mittels der sogenannten Mitternachtsformel:
x1,2 = $\frac{-\mathrm{a_1} \pm \sqrt{\mathrm{a_1}^2 – 4\mathrm{a_2}\ {\cdot}\ \mathrm{a_0}}}{2\ {\cdot}\ \mathrm{a_2}}$
Hierbei muss a12 – 4a2a0 > 0 sein, damit die quadratische Gleichung lösbar ist.
Beispiel:
Es ist folgende quadratische Funktion gegeben:
f(x) = 2x2 – 8x + 6
Hier gilt: a2 = 2, a1 = –8, a0 = 6
Diese Funktion hat daher diese Nullstellen:
x1,2 = $\frac{\mathrm{8} \pm \sqrt{\mathrm{-8}^2 – 4\ {\cdot}\ \mathrm{2}\ {\cdot}\ \mathrm{6}}}{2\ {\cdot}\ \mathrm{2}}$
x1,2 = $\frac{8 \pm \sqrt{64 – 48}}{4}$
x1,2 = $\frac{8 \pm \sqrt{16}}{4}$
x1,2 $\frac{8 \pm 4}{4}$
x1 = $\frac{8}{4}$ – $\frac{4}{4}$ = 2 – 1 = 1
x2 = $\frac{8}{4}$ + $\frac{4}{4}$ = 2 + 1 = 3
Die quadratische Funktion hat die Nullstellen:
x1 = 1 und x2 = = 3
2.3 Ganzrationale Funktionen 3 Grades oder höheren Grades
Liegt eine ganzrationalen 3. Grades oder noch höheren Grades vor, dann kann man deren Nullstellen normalerweise nicht mit einer Formel bestimmen. Nur für Sonderfällt kann man spezielle Lösungsverfahren anwenden:
2.31 Lösen mittels Ausklammern
Es ist diese ganzrationale Funktion 3. Grades gegeben:
f(x) x3 – 4x2 – x
Da die Funktion kein absolutes Glied (also einen Koeffizienten ohne Variable) vorweist, kann man hier das x ausklammern.
x3 – 4x2 – x = 0
x · (x2 – 4x – 1) = 0
Eine Nullstelle ist x = 0, da dann das komplette Produkt gleich null wird. Die anderen Nullstellen kann man nun mittels der Mitternachtsformel ermitteln.
a2 = 1, a1 = –4, a0 = –1
x1,2 = $\frac{\mathrm{-4} \pm \sqrt{\mathrm{4}^2 – 4\ {\cdot}\ \mathrm{1}\ {\cdot}\ \mathrm{(-1)}}}{2\ {\cdot}\ \mathrm{1}}$
x1,2 = $\frac{-4 \pm \sqrt{16 + 4}}{2}$
x1,2 = $\frac{-4 \pm \sqrt{20}}{2}$
x1,2 = $\frac{-4}{2}$ – $\frac{\sqrt{20}}{2}$ = –2 – $\frac{\sqrt{20}}{2}$ = –2 – $\frac{\sqrt{4\ {\cdot}\ 5}}{2}$ = –2 – $\frac{2\sqrt{5}}{2}$ = – 2 – $\sqrt{5}$
x1,2 = $\frac{-4}{2}$ + $\frac{\sqrt{20}}{2}$ = –2 + $\frac{\sqrt{20}}{2}$ –2 + $\frac{\sqrt{4\ {\cdot}\ 5}}{2}$ = –2 + $\frac{2\sqrt{5}}{2}$ = – 2 + $\sqrt{5}$
Die Funktion x3 – 4x2 – x = 0 hat folgende Nullstellen:
x1 = 0, x2 = –2 – $\sqrt{5}$, x3 = –2 + $\sqrt{5}$
2.32 Lösen mittels Substitution
Es ist folgende ganzrationale Funktion 4. Grades gegeben:
f(x) = x4 – 5x2 + 6
Substitution: u = x2
Dadurch ergibt sich diese quadratische Gleichung.
u2 – 5u + 6 = 0
Die Gleichung kann man nun mittels der Mitternachtsformel lösen:
u2 = 1, u1 = –5, u0 = 6
u1,2 = $\frac{\mathrm{5} \pm \sqrt{\mathrm{-5}^2 – 4\ {\cdot}\ \mathrm{1}\ {\cdot}\ \mathrm{6}}}{2\ {\cdot}\ \mathrm{1}}$
u1,2 = $\frac{5 \pm \sqrt{25 – 24}}{2}$
u1,2 = $\frac{5 \pm \sqrt{1}}{2}$
u1,2 = $\frac{5 \pm 1}{2$
u1 = $\frac{5}{2}$ – $\frac{1}{2}$ = $\frac{4}{2}$ = 2
u2 = $\frac{5}{2}$ + $\frac{1}{2}$ = $\frac{6}{2}$ = 3
Jetzt muss man noch eine Resubstitution durchführen: u = x2
2 = x2 | √
x = ± $\sqrt{2}$
3 = x2 | √
x = ± $\sqrt{3}$
Daraus ergeben sich für die Funktion f(x) = x4 – 5x2 + 6 diese Nullstellen:
x1 = –$\sqrt{2}$, x2 = $\sqrt{2}$, x3 = –$\sqrt{3}$, x4 = $\sqrt{3}$