
Hat man in Mathe eine lineare Gleichung vor sich, so zeigt sich hier das spätere Algebra-Können – oder auch nicht. Je nach Aufgabenstellung sollte man nämlich als Schülerin oder als Schüler ganz fix die Gleichung so verändern, dass man im Nu zu der gewünschten Lösung gelangt. Lineare Gleichungen sind ja in der Mathematik die einfachsten Gleichungen und besitzen daher eine sehr überschaubare Komplexität. Deshalb kann man an diesen sich jegliche Problemstellung sehr gut verständlich vor Augen führen – was wiederum sehr hilfreich für komplexere Gleichungen ist. Wie intensiv man sich mit linearen Gleichungen beschäftigt hat und wie hoch der Verständnisgrad ist, zeigt sich dann immer schließlich in der Zeit, die man zum Lösen einer Aufgabe benötigt.
Aufgaben zum Mathematik-Stoffgebiet Lineare Gleichungen
1. Mathe-Nachhilfe-Aufgabe: Löse jeweils möglichst einfach die Gleichung auf!
a) 5 (x + 2) = 30
b) (x – 4) · 3 = 12
c)

d) (x – 7) · 5 = 25
e)

f)

g) 7 · (x – 0,5) = 24,5
h)
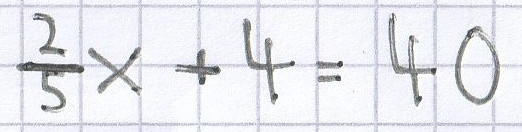
2. Mathematik-Nachhilfe-Aufgabe: Für welches x erfüllt der Term jeweils folgende Werte?
a) 13x + 1 + 5x – 7 Wert: 12; 0; –6; –24
b)

Wert:

; –1; 0
c) –92x + 1 + 100x – 1,2 Wert: 0,6; –8,2; 3,8; –6,2
Lösungen zum Mathe-Stoffgebiet Lineare Gleichungen
1. Mathe-Nachhilfe-Aufgabe: Löse die Aufgabe so, dass sich möglichst schnell die Lösung zeigt.
a) 5 (x + 2) = 30
Hier eliminiert man als Erstes den Faktor vor der Klammer. Dann liegt fast schon die Lösung vor. Um einiges länger würde es dauern, wenn man die Klammer mittels Distributivgesetz/Verteilungsgesetz ausmultipliziert!
a)
5 (x + 2) = 30 | : 5
x + 2 = 6 | – 2
x = 4
L = {4}
b) (x – 4) · 3 = 12
Hier eliminiert man als Erstes wiederum den Faktor. Hierdurch kann man mit Abstand am schnellsten das Ergebnis ermitteln!
b)
(x – 4) · 3 = 12 | : 3
x – 4 = 4 | + 4
x = 8
L = {8}
c)

Hier eliminiert man als Erstes den Bruch, indem man die Gleichung mit dem Nenner des Bruchs malnimmt. Dadurch kürzt sich der Nenner heraus!
c)

x + 6 = 40 | – 6
x = 34
L = {34}
d) (x – 7) · 5 = 25
Hier eliminiert man wiederum zunächst den Faktor vor der Klammer.
d)
(x – 7) · 5 = 25 | : 5
x – 7 = 5 | + 7
x = 12
L = {12}
e)

Hier gilt wieder, dass man am schnellsten zum Ergebnis kommt, wenn man zuerst den Nenner des Bruchs eliminiert.
e)

x – 8 = 21 | + 8
x = 29
L = {29}
f)
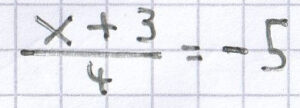
Wenn man hier wiederum als Erstes den Bruch eliminiert, kommt man am schnellsten zur Lösung der Gleichung.
f)
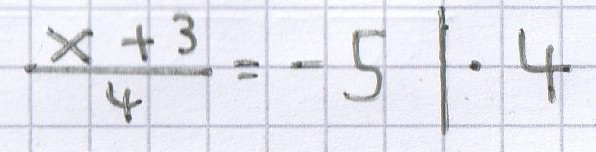
x + 3 = –20 | – 3
x = –23
L = {–23}
g) 7 · (x – 0,5) = 24,5
Hier sollte man auf jeden Fall als Erstes den Faktor vor der Klammer eliminieren.
g)
7 · (x – 0,5) = 24,5 | : 7
x – 0,5 = 3,5 | + 0,5
x = 4
L = {4}
h)

Hier geht man wie gewohnt vor. Zuerst die Variable separieren, dann den Faktor, der vor ihr steht, eliminieren.
h)


x = 90
L = {90}
2. Mathe-Nachhilfe-Aufgabe: Bestimme jeweils das x für die angegebenen Werte.
a) 13x + 1 + 5x – 7 Wert: 12; 0; –6; –24
Bevor man hier eine Gleichung für den jeweils gesuchten Wert aufstellt, sollte man zunächst den angegeben Term vereinfachen.
13x + 1 + 5x – 7 = 18x – 6
Darauf kann man die Gleichung für den gesuchten Wert aufstellen.
18x – 6 = 12 | + 6
18x = 18 | : 18
x = 1
L = {1}
Bei x = 1 wird der Term-Wert 12.
18x – 6 = 0 | + 6
18x = 6 | : 18
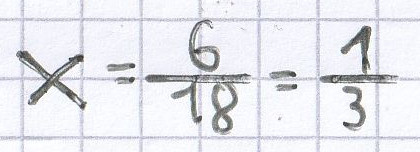
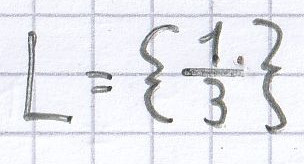
Bei
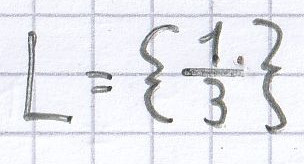
Lösung Gleichung
wird der Term-Wert 0.
18x – 6 = –6 | + 6
18x = 0 | : 18
x = 0
L = {0}
Bei x = 0 wird der Term-Wert –6.
18x – 6 = –24 | + 6
18x = –18 | : 18
x = –1
L = {–1}
Bei x = –1 wird der Term-Wert –24.
b)

Wert:

;–1; 0
Auch hier sollte man zunächst den Term vereinfachen.

Darauf kann man die jeweiligen x für die angegebenen Term-Werte ermitteln.
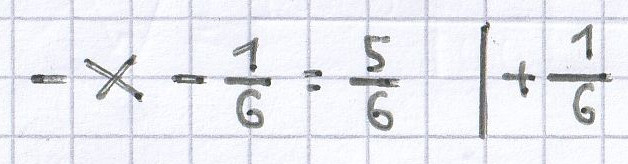
–x = 1 | · (–1)
x = –1
L = {–1}
Bei x = –1 wird der Term-Wert

.
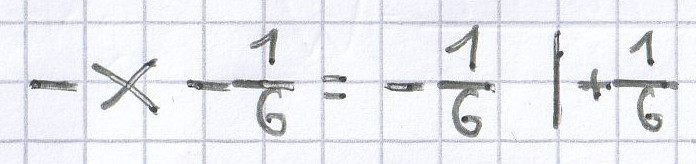
–x = 0 | · (–1)
x = 0
L = {0}
Bei x = 0 wird der Term-Wert

.

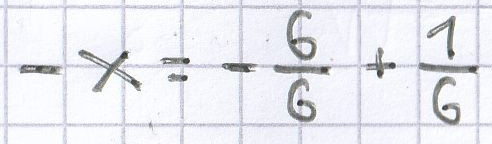
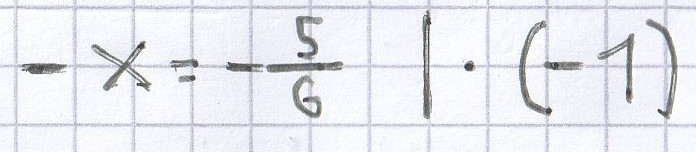

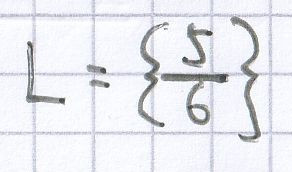
Bei

wird der Term-Wert –1.



Bei

wird der Term-Wert 0.
c) –92x + 1 + 100x – 1,2 Wert: 0,6; –8,2; 3,8; –6,2
Diesen Term sollte man auch vorab vereinfachen.
–92x + 1 + 100x – 1,2 = 8x – 0,2
Danach kann man diejenigen x für die angegebenen Term-Werte bestimmen.
8x – 0,2 = 0,6 | + 0,2
8x = 0,8 | : 8
x = 0,1
L = {0,1}
Bei x = 0,1 erhält man den Term-Wert 0,6.
8x – 0,2 = –8,2 | + 0,2
8x = –8 | : 8
x = –1
L = {–1}
Bei x = –1 wird der Term-Wert –8,2.
8x – 0,2 = 3,8 | + 0,2
8x = 4 | : 8
x = 0,5
Bei x = 0,5 erhält man den Term-Wert 3,8.
8x – 0,2 = –6,2 | + 0,2
8x = –6 | : 8
x = –0,75
L = {–0,75}
Bei x = –0,75 erhält man den Term-Wert –6,2.