
„Hört das denn in Mathe niemals auf mit den binomischen Formeln?“ fragt sich ein innerlich genervter Schüler, als just bei dem Stoffgebiet Quadratische Gleichungen binomischen Formeln wieder aus dem Nichts auftauchen. Unbeantwortete Fragen nerven ja bekanntlich ebenso sehr. Daher möchten wir hier auch keinen Schüler unnötigerweise länger als notwendig damit im Unklaren lassen. Die Antwort zu der an sich selbst gestellten Frage des Schülers ist folgende: bis zum Abitur in Mathematik – dann hat man aber endlich seine Ruhe vor den binomischen Formeln. Trotz jetziger Gewissheit macht das die ganze Sache für den Schüler natürlich nicht wesentlich besser. Korrekt lösen muss er ja in Mathe weiterhin die binomischen Formeln auflösen können. Und das kann man am besten, indem man das übt, übt und nochmals übt.
Aufgaben zum Stoffgebiet Binomische Formeln
1. Mathe-Nachhilfe-Aufgabe: Ermittle die Lösungsmenge.
a) (x – 4)² = (x + 5)²
b) (x + 7) (x – 7) = (x + 8)² – 1
c) –(x + 9)² + (x – 11)² = 0
d) (2x + 5) (8x – 3) – 5 = (4x – 1)²
e)
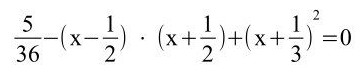
f) (3x –8) (3x + 8) – (x + 1,2) (9x – 5) = –87
g) (1,5x – 3,2)² – 38,08 = (1,5x + 2,4)²
h)
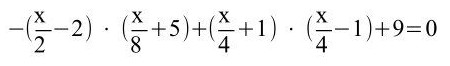
2. Mathematik-Nachhilfe-Aufgabe: Bestimme die Lösungsmenge.
a) (x – 2) · (x + 7) = (x + 1)²
b) (6 – 2a)² = (2a – 4)² – 36
c) (2x – 7)² + 9 = 4x² – 9x + 1
d) 6y + (4 – y)² = –(24 – y²)
e) (y – 5) · (y + 3) – y = (y – 3)²
f) (1 + 2x)² – 30x – 14 = (2x – 15)²
g) (1 + 3z)² + 8z + 1 = (2 + 3z)²
h) (3 – x)² + 5x = (x + 2) · (3 + x)
i) (t + 3) (t – 3) + 2 = (t – 7)²
j) (3 + 2t) (1 – 8t) + 20 = (1 – 4t) (1 + 4t)
3. Mathe-Nachhilfe-Aufgabe: Fülle die Unterstriche innerhalb der Gleichung aus.
a) (4a + _)² = _ + _ + 64
b) (_ – 6)² = _ – 96y + _
c) (_ + _)² = 9a² + 24a + _
d) (_ + _)² = _ + 720a + 400
e) (_ – _)² = 144a² – 96a + _
f) (_ – _) · (_ + _) = 144x² – 36y²
g) (_ – 3a) · (_ + _) = – _ + 4x²
h) (12 + _) · (_ – _) = _ – 400q²
4. Mathe-Nachhilfe-Aufgabe: Faktorisiere und ziehe hierfür die binomischen Formeln heran.
a) x² + 2xy + y²
x² + 2x · 7 + 49
a² – 2ab + b²
r² – 2rs + s²
b) x² + 20x + 100
a² – 20a + 100
x² – 2x + 1
a² + 14a + 49
c) 25 + a² – 10a
36 + x² + 12x
100 + b² – 20b
169 + x² – 26x
d) a² – b²
u² – 121v²
1 – 16r²
s² – 625
Lösungen zum Mathematik-Stoffgebiet Binomische Formeln
1. Mathe-Nachhilfe-Aufgabe: Bestimme die Lösungsmenge.
a) (x – 4)² = (x + 5)²
Hier muss man erkennen, dass sowolh die 2. Binomische Formel als auch die 1. Binomische Formel vorliegen
x · x + 2 · x · (–4) + (–4) · (–4) = x · x + 2 · x · 5 + 5 · 5
x² –8x + 16 = x² + 10x + 25 | – x²
–8x + 16 = 10x + 25 | – 10x
–18x + 16 = 25 | – 16
–18x = 9 | : (–18)
x = –0,5
L = {–0,5}
b) (x + 7) (x – 7) = (x + 8)² – 1
Hier muss man erkennen, dass sowohl die 3. Binomische Formel vorliegt als auch die 1. Binomische Formel.
x · x + 7 · (–7) = x · x + 2 · x · 8 + 8 · 8 – 1
x² – 49 = x² + 16x + 64 – 1
x² – 49 = x² + 16x + 63 | – x²
–49 = 16x + 63 | – 63
–112 = 16x | : 16
–7 = x
L = {–7}
c) –(x + 9)² + (x – 11)² = 0
Hier muss man sehen, dass die 1. Binomische Formel und die 2. Binomische Formel vorliegen. Auch muss man erkennen, dass vor der 1. Binomischen Formel sich ein Minus befindet und hier eine Minusklammer vorliegt.
–(x · x + 2 · x · 9 + 9 · 9) + x · x + 2 · x · (–11) + (–11) · (–11) = 0
–(x² + 18x + 81) + x² – 22x + 121 = 0
–x² – 18x – 81 + x² – 22x + 121 = 0
–40x + 40 = 0 | + 40
40 = 40x | : 40
1 = x
L = {1}
d) (2x + 5) (8x – 3) – 5 = (4x –1)2
Hier muss man erkennen, dass nur die 1. Binomische Formel vorliegt. Die beiden anderen Klammen muss man über das Distributivgesetz/Verteilungsgesetz hin auflösen.
2x · 8x + 2x · (–3) + 5 · 8x + 5 · (–3) – 5 = 4x · 4x + 2 4x · (–1) + (–1) · (–1)
16x² – 6x + 40x – 15 – 5 = 16x² – 8x + 1
16x² + 34x – 20 = 16x² – 8x + 1 | – 16x²
34x – 20 = – 8x + 1 | + 8x
42x – 20 = 1 | + 20
42x = 21 | + 42
x = 0,5
L = {0,5}
e)
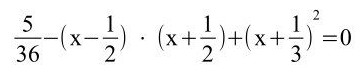
Hier muss man erkennen, dass die 3. und 1. Binomisch Formel vorliegen sowie eine Minusklammer vor der 3. Binomischen Formel.
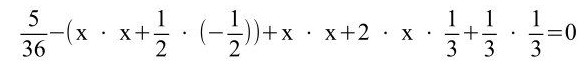
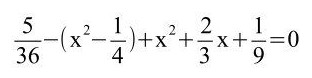
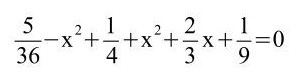
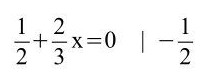
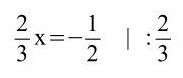
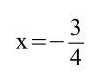
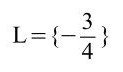
f) (3x –8) (3x + 8) – (x + 1,2) (9x – 5) = –87
Hier muss man sehen, dass die 3. Binomische Formel vorliegt und die anderen beiden Klammern mittels des Distributivgesetzes/Verteilungsgesetzes aufgelöst werden müssen und davor sich noch eine Minusklammer befindet.
3x · 3x + 8 · (–8) – (x · 9x + x · (–5) + 1,2 · 9x + 1,2 · (–5)) = – 87
9x² – 64 – (9x² – 5x + 10,8x – 6) = –87
9x² – 64 – 9x² + 5x – 10,8x + 6 = –87
–58 – 5,8x = –87 | + 58
–5,8x = –29 | : (–5,8)
x = 5
L = {5}
g) (1,5x – 3,2)² – 38,08 = (1,5x + 2,4)²
Hier muss man erkennen, dass sowohl die 2. Binomische Formel als auch die 1. Binomisch Formel vorliegen.
1,5x · 1,5x + 2 · 1,5x · (–3,2) + (–3,2) · (–3,2) – 38,08 = 1,5 · 1,5x + 2 · 1,5x · 2,4 + 2,4 · 2,4
2,25x² – 9,6x + 10,24 – 38,08 = 2,25x² + 7,2x + 5,76
2,25x² – 9,6x – 27,84 = 2,25x² + 7,2x + 5,76 | – 2,25x²
– 9,6x – 27,84 = 7,2x + 5,76 | + 9,6x
–27,84 = 16,8x + 5,76 | – 5,76
–33,6 = 16,8x | : 16,8
–2 = x
L = {–2}
h)
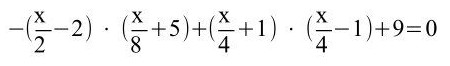
Hier muss man erkennen, dass die ersten beiden Klammern mittels des Distributivgesetzes/Verteilungsgesetzes aufgelöst werden müssen sowie davor sich noch eine Minusklammer befindet. Bei den anderen beiden liegt die 3. Binomische Formel vor.
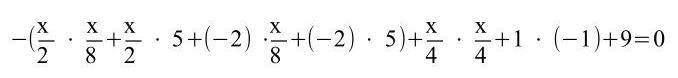
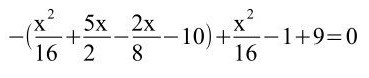
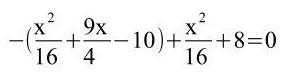
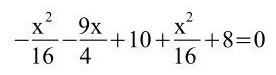
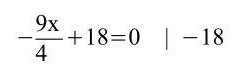
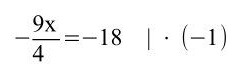
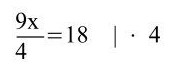
9x = 72 | : 9
8 = x
x = 8
L = {8}
2. Mathe-Nachhilfe-Aufgabe: Ermittle die Lösungsmenge.
a) (x – 2) · (x + 7) = (x + 1)²
x · x + x · 7 + (–2) · x + (–2) · 7 = x · x + 2 · x · 1 + 1 · 1
x² + 7x – 2x – 14 = x² + 2x + 1
x² + 5x – 14 = x² + 2x + 1 | – x²
5x – 14 = 2x + 1 | – 2x
3x – 14 = 1 | + 15
3x = 15 | : 2
x = 5
L = {5}
b) (6 – 2a)² = (2a – 4)² – 36
6 · 6 + 2 · 6 · (–2a) + (–2a) · (–2a) = 2a · 2a + 2 · 2a · (–4) + (–4) · (–4) – 36
36 – 24a + 4a² = 4a² – 16a + 16 – 36
36 – 24a + 4a² = 4a² – 16a – 20 | – 4a²
36 – 24a = – 16a – 20 | + 24a
36 = 8a – 20 | + 20
56 = 8a | : 8
7 = a
L = {7}
c) (2x – 7)² + 9 = 4x² – 9x + 1
2x · 2x + 2 · 2x · (–7) + (–7) · (–7) + 9 = 4x² – 9x + 1
4x² – 28x + 58 = 4x² – 9x + 1 | – 4x²
– 28x + 58 = –9x + 1 | + 28x
58 = 19x + 1 | – 1
57 = 19x | : 19
3 = x
L = {3}
d) 6y + (4 – y)² = –(24 – y²)
6y + 4 · 4 + 2 · 4 · (–y) + (–y) · (–y) = –24 + y²
6y + 16 – 8y + y² = –24 + y²
–2y + 16 + y² = –24 + y² | – y²
–2y + 16 = –24 | – 16
–2y = – 40 | : 2
y = 20
L = {20}
e) (y – 5) · (y + 3) – y = (y – 3)²
y · y + y · 3 + (–5) · y + (–5) · 3 – y = y · y + 2 · y · (–3) + (–3) · (–3)
y² + 3y – 5y – 15 – y = y² – 6y + 9
y² – 3y – 15 = y² – 6y + 9 | – y²
–3y – 15 = –6y + 9 | + 6y
3y – 15 = 9 | + 15
3y = 24 | : 3
y = 8
L = {8}
f) (1 + 2x)² – 30x – 14 = (2x – 15)²
1 · 1 + 2 · 1 · 2x + 2x · 2x – 30x – 14 = 2x · 2x + 2 · 2x · (–15) + (–15) · (–15)
1 + 4x + 4x² – 30x – 14 = 4x² – 60x + 225
–13 – 26x + 4x² = 4x² – 60x + 225 | – x²
–13 – 26x = –60x + 225 | + 60x
–13 + 34x = 225 | + 13
34x = 238 | : 34
x = 7
L = {7}
g) (1 + 3z)² + 8z + 1 = (2 + 3z)²
1 · 1 + 2 · 1 · 3z + 3z · 3z + 8z + 1 = 2 · 2 + 2 · 2 · 3z + 3z · 3z
1 + 6z + 9z² + 8z + 1 = 4 + 12z + 9z²
2 + 14z + 9z² = 4 + 12z + 9z² | – 9z²
2 + 14z = 4 + 12z | – 12z
2 + 2z = 4 | – 2
2z = 2 | : 2
z = 1
L = {1}
h) (3 – x)² + 5x = (x + 2) · (3 + x)
3 · 3 + 2 · 3 · (–x) + (–x) · (–x) + 5x = x · 3 + x · x + 2 · 3 + 2 · x
9 – 6x + x² + 5x = 3x + x² + 6 + 2x
9 – x + x² = 5x + x² + 6 | – x²
9 – x = 5x + 6 | – 5x
9 – 6x = 6 | – 9
–6x = –3 | : ( –3)
x = 0,5
L = {0,5}
i) (t + 3) (t – 3) + 2 = (t – 7)²
t · t + 3 · (–3) + 2 = t · t + 2 · t · (–7) + (–7) · (–7)
t² – 9 + 2 = t² –14t + 49
t² – 7 = t² –14t + 49 | – t²
–7 = –14t + 49 | – 49
–56 = –14t | : (–14)
4 = t
L = {4}
j) (3 + 2t) (1 – 8t) + 20 = (1 – 4t) (1 + 4t)
3 · 1 + 3 · (–8t) + 2t · 1 + 2t · (–8t) + 20 = 1 · 1 + (–4t) · 4t
3 – 24t + 2t – 16t² + 20 = 1 – 16t²
23 – 22t – 16t² = 1 – 16t² | + 16t²
23 – 22t = 1 | –23
–22t = –22 | : (–22)
t = 1
L = {1}
3. Mathe-Nachhilfe-Aufgabe: Fülle die Unterstriche innerhalb der Gleichung korrekt aus.
a) (4a + _)² = _ + _ + 64
Hier handelt es sich um die 1. Binomische Formel. Durch das Wurzelziehen des „64“ erhält man den zweiten Term der unaufgelösten binomischen Formel. Darauf kann man die restlichen Terme in der aufgelösten Form bestimmen.
(4a + 8)² = 16a² + 64a + 64
b) (_ – 6)² = _ – 96y + _
Hier liegt die 2. Binomische Formel vor. Indem man den Mittelterm „– 96y“ durch „2“ und durch „–6“ teilt, erhält man den ersten Term der unaufgelösten binomischen Formel. Daraufhin kann man die 2. Binomische Form in der aufgelösten Form bilden.
(8y – 6)² = 64y² – 96y + 36
c) (_ + _)² = 9a² + 24a + _
Hier liegt die 1 Binomische Formel vor. Dadurch dass man beim „9a²“ die Wurzel zieht, erhält man den 1. Term der Binomischen Formel in der unaufgelösten Form. Darauf kann man dem Mittelterm „24a“ durch „2“ und „3a“ teilen, um den zweiten Term in der unaufgelösten Form zu erhalten. Darauf kann man die Binomische Formel in die unaufgelöste Form bringen.
(3a + 4)² = 9a² + 24a + 16
d) (_ + _)² = _ + 720a + 400
Hier liegt die 1. Binomische Formel vor. Indem man von „400“ die Wurzel zieht, erhält man den zweiten Term in der unaufgelösten Form. Darauf kann man den Mittelterm „720a“ durch „2“ und „20“ teilen, wodurch man den ersten der unaufgelösten Form erhält. Anschließend kann man die unaufgelöste Form der binomischen Formel in die aufgelöste Form umwandeln.
(18a + 20)² = 324a² + 720a + 400
e) (_ – _)² = 144a² – 96a + _
Hier liegt die 2. Binomische Formel vor. Indem man bei „144a²“ die Wurzel zieht, erhält man den ersten Term in der unaufgelösten Form. Teilt man „–96a“ durch „2“ und „12a“, so erhält man den zweiten Term in der unaufgelösten Form. Daraufhin kann man die 2. Binomische Formel von der unaufgelösten Form hin zur aufgelösten umwandeln.
(12a – 4)² = 144a² – 96a + 16
f) (_ – _) · (_ + _) = 144x² – 36y²
Hier liegt die 3. Binomische Formel vor. Dadurch, dass man bei „144x²“ und „36y²“ die Wurzel zieht, erhält man jeweils die beiden Terme in der unaufgelösten Form.
(12x – 6) · (12x + 6) = 144x² – 36y²
g) (_ – 3a) · (_ + _) = – _ + 4x²
Hier liegt die 3. Binomische Formel vor. „3a“ ist hierbei der eine Term in der unaufgelösten Form. Zieht man bei „4x²“ die Wurzel, so erhält man den zweiten Term in der unaufgelösten Form.
(2x – 3a) · (2x + 3a) = – 9a² + 4x²
h) (12 + _) · (_ – _) = _ – 400q²
Hier liegt die 3. Binomische Formel vor. Indem man bei „400q²“ die Wurzel zieht, erhält man den zweiten Term in der unaufgelösten Form.
(12 + 20q) · (12 – 20q) = 144 – 400q²
4. Mathematik-Nachhilfe-Aufgabe: Faktorisiere mittels der Zuhilfenahme der binomischen Formeln.
a) x² + 2xy + y²
Hier liegt die 1. Binomische Formel vor.
(x + y) · (x + y) = (x + y)²
a) x² + 2x · 7 + 49
Hier handelt es sich um die 1 Binomische Formel.
(x + 7) · (x + 7) = (x + 7)²
a) a² – 2ab + b²
Hier liegt die 2. Binomisch Formel vor.
(a – b) · (a – b) = (a – b)²
a) r² – 2rs + s²
Hier liegt ebenfalls die 2. Binomische Formel vor.
(r – s) · (r – s) = (r – s)²
b) x² + 20x + 100
Hier liegt die 1. Binomische Formel vor.
(x + 10) · (x + 10) = (x + 10)²
b) a² – 20a + 100
Hier handelt es sich um die 2. Binomische Formel.
(a – 10) · (a – 10) = (a – 10)²
b) x² – 2x + 1
Hier liegt ebenfalls die 2. Binomische Formel vor.
(x – 1) · (x – 1) = (x – 1)²
b) a² + 14a + 49
Hier handelt es sich um die 1. Binomische Formel.
(a + 9) · (a + 7) = (a + 7)²
c) 25 + a² – 10a
Hier liegt ebenfalls die 2. Binomische Formel vor.
(5 – a) · (5 – a) = (5 – a)²
c) 36 + x² + 12x
Hier handelt es sich um die 1. Binomische Formel.
(6 + x) · (6 + x) = (6 + x)²
c) 100 + b² – 20b
Hier liegt die 2. Binomische Formel vor.
(10 – b) · (10 – b) = (10 – b)²
c) 169 + x² – 26x
Hier handelt es sich ebenfalls um die 2. Binomische Formel.
(13 – x) · (13 – x) = (13 – x)²
d) a² – b²
Hier liegt die 3. Binomische Formel vor.
(a + b) · (a – b)
d) u² – 121v²
Hier liegt ebenfalls die 3. Binomische Formel vor.
(u + 11v) · (u – 11v)
d) 1 – 16r²
Hier handelt es sich ebenso um die 3. Binomische Formel.
(1 + 4r) · (1 – 4r)
d) s² – 625
Hier liegt auch die 3. Binomische Formel vor.
(s + 25) · (s – 25)