1. Allgemeines zum Kreisdiagramm
Das Kreisdiagramm (auch wegen seines Aussehens oft auch als Tortendiagramm bezeichnet) stellt eine Diagrammart dar, die Schülerinnn in der Regel erst in der Sekundarstufe I anfertigen. Das liegt an dem erhöhten Schwierigkeitsgrad, ein Kreisdiagramm zu machen. Man muss zum einen mit dem Zirkel umgehen und zum anderen die Anteile in Prozentangaben umrechnen können. Darüber hinaus ist es notwendig, die Prozentangaben in Gradwerte umzurechnen und diese mittels des Geodreiecks korrekt in den Kreis einzuzeichnen. Wie man unschwer sieht, muss man schon einige mathematische Fertigkeiten beherrschen, um ein Kreisiagramm anfertigen zu können.
Kreisdiagramm eignen sich besonders gut, um die Merkmalausprägungen zu einem bestimmten Merkmal deutlich voneinander abzugrenzen. Denn durch die einzelnen Sektoren im Kreisdiagramm wird die einzelnen Merkmalausprägungen besonders ersichtlich.
2. Anfertigung eines Kreisdiagramms
Eine Erhebung zum Lieblings-Freizeitverhalten von Kindern, bei der 40 Kinder gefragt wurden, ergab folgende Ergebnisse.
Sport treiben: 12 Personen,
Fernsehen: 8 Personen
Lesen: 6 Personen
Video spielen: 10 Personen
Freunde treffen: 4 Personen
Zunächst muss man die Begriffe das Ganze und der Anteil, die aus der Bruchrechnung stammen, auf die Erhebung anwenden. Das ist vonnöten, da man diese rechnerisch, die Anteile zum Ganzen, bestimmen muss. Das Ganze sind alle Kinder, also 40. Der Anteil sind die Anzahl an Kinder, die eine bestimme Merkmalausprägung als Lieblings-Freizeitverhalten angegeben haben, also 12 Personen bei Sport treiben, 8 Personen bei Fersehen, 6 Personen bei Lesen, 10 Personen, bei Video spielen und 4 Personen bei Freunde treffen.
Dieses Verhältnis Anteile zum Ganzen in Prozent kann man nun rechnerisch folgendermaßen mittels bestimmen:
12/40 = 3/10 = 0,3= 30 %
8/40 = 1/5 = 0,2 = 20 %
6/40 = 3/20 = 0,15 = 15 %
10/40 = 1/4 = 0,25 = 25 %
4/40 = 1/10 = 0,1 = 10 %
Im nächsten Schritt muss man die jeweiliges Prozentangabe des Anteils zum Ganzen in Grad umrechnen. Ein vollständiger Kreis hat bekanntlich 360°. Die Anteile zum Ganzen setzt man nun in Beziehung dazu. Hierbei zieht man am besten den Dreisatz heran. Denn es es besteht hier folgende Zuordnung:
360° – 100 %
? – 30 %
? – 20 %
? – 15 %
? – 25 %
? – 10 %
Es handelt sich hier um proportionale Zuordnungen. Daher kann man die fehlenden Grad-Werte zu dem jeweiligen Prozentwert einfach durch Umformung der Grundzuordung bestimmen. Am schnellsten und einfachsten geht das, wenn man bestimmt, wie viel Grad 1 % entsprechen. Dafür teilt man die Anfangszuordnung durch 100. Darauf nimmt man die erhalten Zuordnung mit der Prozentangabe mal, die man bestimmt hat.
360° – 100 % | : 100
3,6° – 1 % | · 30
108° – 30 %
3,6° – 1 % | · 20
72° – 20 %
3,6° – 1 % | · 15
54° – 15 %
3,6° – 1 % | · 25
90° – 25 %
3,6° – 1 % | · 10
36° – 10 %
Jetzt zeichnet man mit einem Zirkeln einen größeren Kreis mit einem Radius von 5 bis 7 cm Radius, damit die Anteile gut einzeichnen kann und diese auch gut zur Geltung kommen. An einer beliebigen Stelle innerhalb der Kreises zeichnet man den Radius ein. An diesen Strich legt man das Geodreick an und bestimmt die jeweilige Gradzahl des Anteils. Hat man eine Gradzahl bestimmt, zeichnet man hierzu eine neue Radius-Linie. Daran legt man wieder das Geodreieck an und bestimmt die nächste Gradzahl des Anteils. Wenn man diesee wiederum bestimmt hat, zeichnet man hierzu wieder eine neue Radius Linie. Auf die gleiche Weise fährt man fort, bis man alle Anteile in Grad bestimmt hat und die einzelnen Sektoren mittels Radius-Linie voneinander abgetrennt hat. Ganz am Ende macht man in der Nähe des jeweiligen Sektor die Beschriftung, das heißt, dass man die jeweilige Merkmalausprägung nennt.
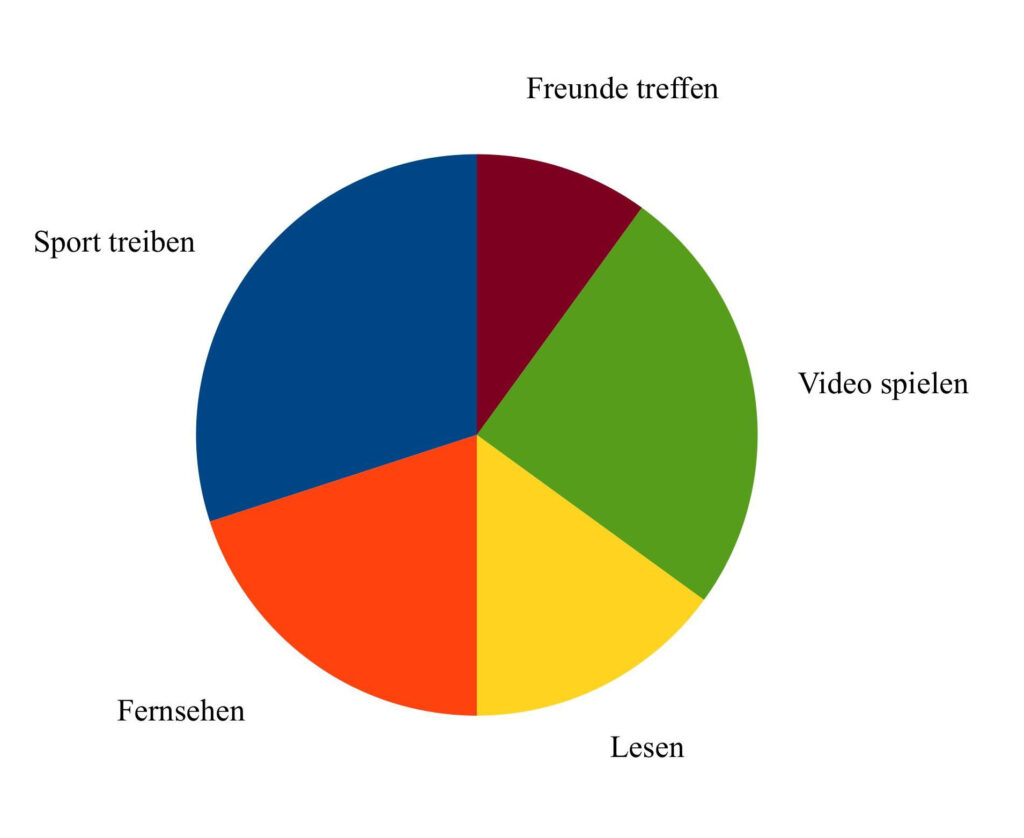
Anhand des Keisdiagrammes kann man nun sofort sehr gut die einzelnen Merkmalausprägungen sehen.