1. Allgemeines zum Baumdiagramm
Ein Baumdiagramm dient dazu, bildlich alle Ergebnisse und deren Wahrscheinlichkeiten eines Wahrscheinlichkeitsexperiments übersichtlich darzustellen. Sämtliche Ereignisse und Abfolgen lassen sich hier Schritt für Schritt optisch verdeutlichen. Die hierbei auftretenden Wahrscheinlichkeiten kann man exakt entlang der einzelnen Äste berechnen.
In der Grundschule wird normalerweise ein Baumdiagramm ausschließlich mit den möglichen Kombinationsmöglichkeiten (und ohne die Prozentangaben der Wahrscheinlichkeiten an den Ästen) erstellt, da Kinder in diesem Alter bereits ein Verständnis für ein bestimmtes kombinatorisches Phänomen haben.
2. Anfertigung enes Baumdiagramms
Beispiel:
Es soll eine Münze dreimal geworfen werden. Die hierbei auftretenden Möglichkeiten Zahl (Z) oder Kopf (K) sollen anhand eines Baumdiagrammes dargestellt werden.
Als Erstes zeichnet man die beiden Äste nach dem ersten Münzwurf. Es bietet sich hier entweder ein hierarische Anordnung (von oben nach unten) oder eine von links nach rechts an. In diesem Beispiel wird eine hierarische bevorzugt. Bei den beiden ersten Ästen ist es wichtig, dass recht lang sind und einen größeren spitzen Winkel aufweisen, sodass man alles darauffolgenden darunter noch gut einzeichnen kann. Auch ist es wichtig, dass diese möglichst symmetrisch verlaufen. Ist man damit fertig, dann mach man an dem Ende beider Äste einen Kreis. In den einen Kreis schreibt man ein K für Kopf und in den anderen eine Z für Zahl. Diese Verästelung soll Kombinationsmöglichkeit nach dem 1. Münzwurf darstellen.
Jetzt macht man bei dem K wiederum zwei Äste mit einem nicht mehr ganz so groß verlaufendem spitzen Winkel. Das Gleiche macht man bei dem Z. Am Ende des ersten Astes schreibt man widerum ein K, am Ende des zweiten ein Z, am Ende des dritten ein K und am Ende des vierten ein Z. Diese Verästelungen sollen die Kombinationsmöglichkeiten nach dem 2. Münzwurf darstellen.
Darauf macht man bei dem K wiederum zwei Äste mit einem nicht mehrganz so groß verlaufendem spitzen Winkel, das Gleiche macht man bei dem Z und allen anderen Kreisen mit Buchstaben. Diese Verästellungen sollen die Kombinationsmöglichkeiten nach dem 3. Münzwurf darstellen.
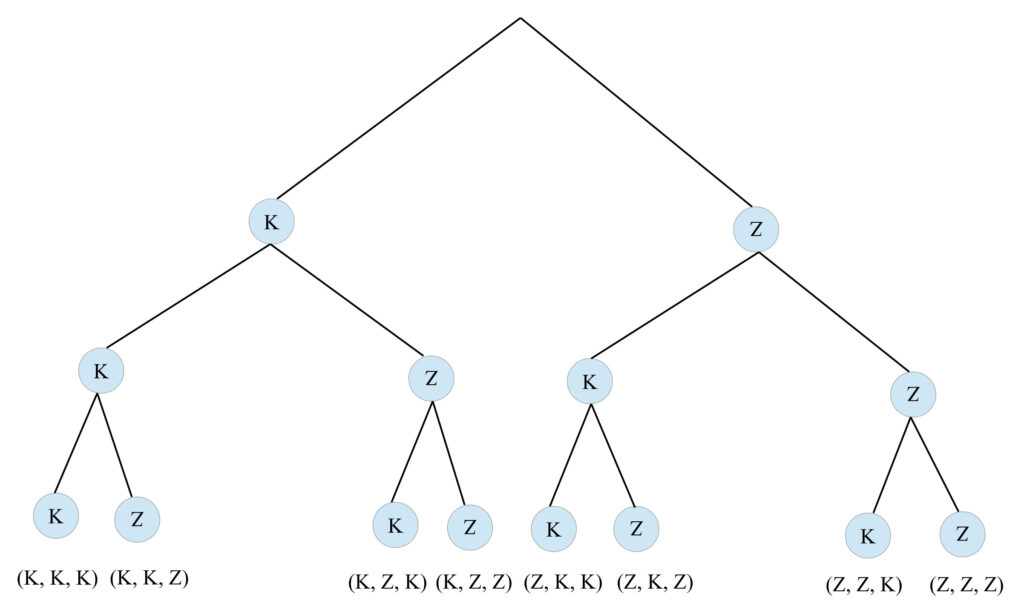
Am Ende fügt man nun unterhalb den acht Kreisen die auftretenden Kombinationsmöglichkeiten der Münze ein (die einzelnen Buchstaben schreibt man in Klammer und trennt diese durch Kommas). Diese ergeben sich, wenn man die einzelnen Äste von oben nach unten entlanggeht. Von links nach rechts ergeben sich dadurch diese Kombinationsmöglichkeiten:
(K, K, K), (K, K, Z) (KZK), (K, Z, Z), (Z, K, K), (Z, K, Z), (Z, Z, K), (Z, Z; Z)
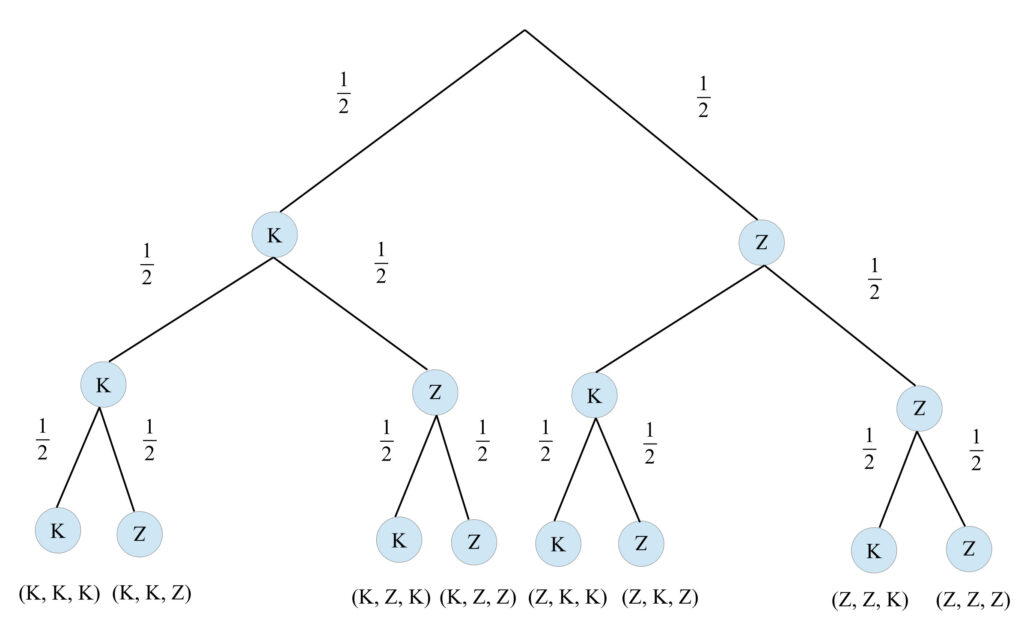
Bei dem folgenden Baumdiagramm wurden zusätzlich die Wahrscheinlichkeiten als Bruchzahlen bei den jeweiligen Verästelungen eingetragen.