1. Die trigonometrischen Beziehungen am rechtwinkligen Dreieck
Ein rechtwinkliges Dreieck besteht bekanntermaßen aus einer Hypotenuse, die sich jeweils gegenüber dem rechten Winkel befindet und zwei Katheten. Hierbei ist die Hypotenuse immer die längste Seite des Dreiecks. Die anderen beiden Seiten bilden stets die Katheten. Je nach Blickrichtung, vom jeweiligen Winkel aus gesehen, werden die beiden Katheten in eine Gegenkathete und eine Ankathete unterteilt. Die Ankathete liegt dabei stets gegenüber der Gegenkathete.
Schaut man daher von der Blickrichtung des Winkels α aus, so befindet sich direkt gegenüber dem Winkel die Gegenkathete (auf dem Bild ist das die Seitenlänge a). Der Gegenkathete gegenüber befindet sich die Ankathete (auf dem Bild ist das die Seitenlänge b). Ist hingegen die Blickrichtung der Winkel β, dann ist die Gegenkathete die dem Winkel gegenüberliegende Seite (auf dem Bild ist das die Seitenlänge b). Die Ankathete (auf dem Bild die Seitenlänge a) ist gegenüber der Gegenkathete liegend.
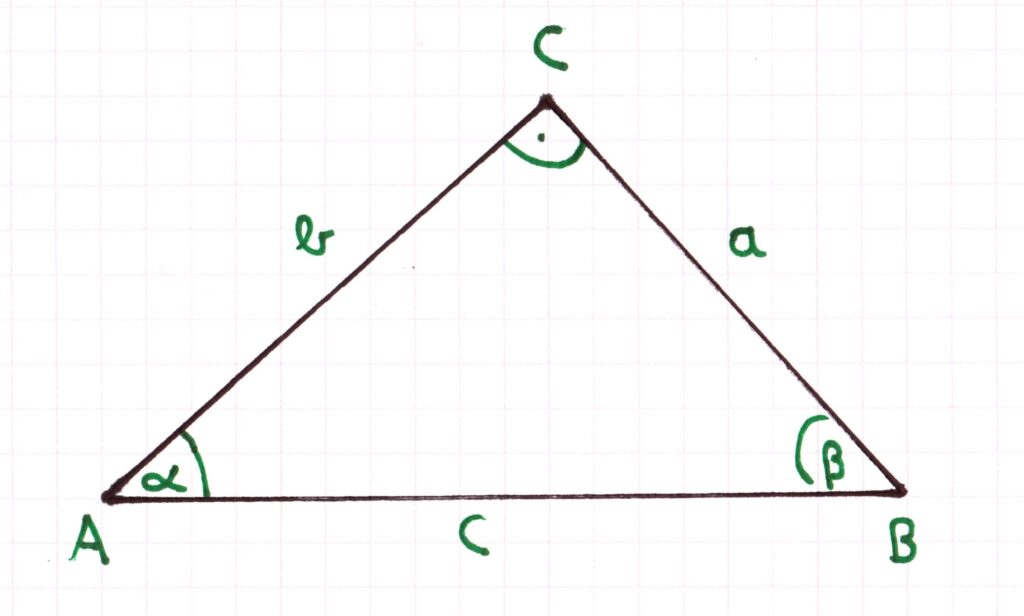
An jedem rechtwinkligen Dreieck sind nun folgende trigonometrischen Beziehungen definiert, von der Blickrichtung des Winkels α:
sin α = ${\frac{\mathrm G\mathrm e\mathrm g\mathrm e\mathrm n\mathrm k\mathrm a\mathrm t\mathrm h\mathrm e\mathrm t\mathrm e }{\mathrm H\mathrm y\mathrm p\mathrm o\mathrm t\mathrm e\mathrm n\mathrm u\mathrm s\mathrm e}}$ = ${\frac{a }{c}}$
cos α = ${\frac{\mathrm A\mathrm n\mathrm k\mathrm a\mathrm t\mathrm h\mathrm e\mathrm t\mathrm e}{\mathrm H\mathrm y\mathrm p\mathrm o\mathrm t\mathrm e\mathrm n\mathrm u\mathrm s\mathrm e}}$ = ${\frac{b}{c}}$
tan α = ${\frac{\mathrm G\mathrm e\mathrm g\mathrm e\mathrm n\mathrm k\mathrm a\mathrm t\mathrm h\mathrm e\mathrm t\mathrm e}{\mathrm A\mathrm n\mathrm k\mathrm a\mathrm t\mathrm h\mathrm e\mathrm t\mathrm e}}$ = ${\frac{a}{b}}$
Und von der Blickrichtung des Winkels β aus gelten in jedem rechtwinkligen Dreieck folgende Beziehungen:
sin β = ${\frac{\mathrm G\mathrm e\mathrm g\mathrm e\mathrm n\mathrm k\mathrm a\mathrm t\mathrm h\mathrm e\mathrm t\mathrm e }{\mathrm H\mathrm y\mathrm p\mathrm o\mathrm t\mathrm e\mathrm n\mathrm u\mathrm s\mathrm e}}$ = ${\frac{\mathrm b }{\mathrm c}}$
cos β = ${\frac{\mathrm A\mathrm n\mathrm k\mathrm a\mathrm t\mathrm h\mathrm e\mathrm t\mathrm e}{\mathrm H\mathrm y\mathrm p\mathrm o\mathrm t\mathrm e\mathrm n\mathrm u\mathrm s\mathrm e}}$ = ${\frac{\mathrm a}{\mathrm c}}$
tan β = ${\frac{\mathrm G\mathrm e\mathrm g\mathrm e\mathrm n\mathrm k\mathrm a\mathrm t\mathrm h\mathrm e\mathrm t\mathrm e}{\mathrm A\mathrm n\mathrm k\mathrm a\mathrm t\mathrm h\mathrm e\mathrm t\mathrm e}}$ = ${\frac{\mathrm b}{\mathrm a}}$
Je nach Blickrichtung vom Winkel α oder vom Winkel β ausgehend, ändert sich beim Aufstellen der jeweiligen trigonometrischen Beziehung die Position der Gegenkathete und der Ankathete am Dreieck. Nur die Hypotenuse bleibt, unabhängig von der Blickrichtung des Winkels, immer an der gleichen Stelle, nämlich gegenüber der dem rechten Winkel.
2. Trigonometrischen Beziehungen: Anwendungsbeispiele
1. Beispiel: In einem Dreieck ABC mit γ = 90° sind zudem folgende Längen gegeben:
α = 35° und c = 6,7 cm.
Berechne die fehlende Längen a und b.
Da die Seitenlänge c gegeben ist und diese sich gegenüber dem rechten Winkel befindet, ist Länge der Hypotenuse bekannt. Gesucht sind demzufolge die beiden Katheten des rechtwinkligen Dreiecks. Von der Blickrichtung des Winkels α ausgehend, kann man diese mittels der trigonometrischen Beziehungen folgendermaßen bestimmen:
sin α = ${\frac{\mathrm G\mathrm e\mathrm g\mathrm e\mathrm n\mathrm k\mathrm a\mathrm t\mathrm h\mathrm e\mathrm t\mathrm e }{\mathrm H\mathrm y\mathrm p\mathrm o\mathrm t\mathrm e\mathrm n\mathrm u\mathrm s\mathrm e}}$ = ${\frac{a }{c}}$
Diese Gleichung muss man nun nach der Seitenlänge a hin auflösen.
sin α = ${\frac{\mathrm a }{\mathrm c}}$ | · c
sin α · c = a
a = sin α · c
a = sin 35° · 6,7 cm
a = 3,8 cm (gerundet auf eine Nachkommastelle)
cos α = ${\frac{\mathrm A\mathrm n\mathrm k\mathrm a\mathrm t\mathrm h\mathrm e\mathrm t\mathrm e}{\mathrm H\mathrm y\mathrm p\mathrm o\mathrm t\mathrm e\mathrm n\mathrm u\mathrm s\mathrm e}}$ = ${\frac{\mathrm b}{\mathrm c}}$
Diese Gleichung muss man nun nach der Seitenlänge b hin auflösen.
cos α = ${\frac{\mathrm b}{\mathrm c}}$ | · c
cos α · c = b
b = cos α · c
b = cos 35° · 6,7 cm
b = 5,5 cm (gerundet auf eine Nachkommastelle)
Die Lösung der Aufgabe aus der Blickrichtung des Winkels β liefert dasselbe Ergebnis für die gesuchten Seitenlängen. Dazu muss man aber noch die Größe dieses Winkels bestimmen. Das kann man aber ganz einfach, da die Winkelsumme in einem Dreieck immer 180° beträgt. Demzufolge ist β = 180° – (α + γ).
2. Beispiel: In einem rechtwinkligen Dreieck ABC ist β = 47° und γ = 90° und die Seitenlänge c = 6,7 cm.
Berechne die Seitenlänge a und b des rechtwinkligen Dreiecks.
Die Hypotenuse, die gegenüber des rechten Winkels sich befindet, ist hier c. Demzufolge sind die beiden gesuchten Seitenlängen a und b die Katheten des Dreiecks. Von der Blickrichtung des Winkels β aus gesehen, ergeben sich hierbei folgende trigonometrischen Beziehungen.
sin β = ${\frac{\mathrm G\mathrm e\mathrm g\mathrm e\mathrm n\mathrm k\mathrm a\mathrm t\mathrm h\mathrm e\mathrm t\mathrm e }{\mathrm H\mathrm y\mathrm p\mathrm o\mathrm t\mathrm e\mathrm n\mathrm u\mathrm s\mathrm e}}$ = ${\frac{\mathrm b }{\mathrm c}}$
Diese Gleichung muss man nun nach der Seitenlänge b hin auflösen.
sin β = ${\frac{\mathrm b }{\mathrm c}}$ | · c
sin α · c = b
b = sin α · c
b = sin 47° · 6,7 cm
b = 4,9 cm (gerundet auf eine Nachkommastelle)
cos β = ${\frac{\mathrm a }{\mathrm c}}$ | · c
cos β · c = a
a = cos β · c
a = cos 47° · 6,7 cm
a = 4,6 cm (gerundet auf eine Nachkommastelle)
Die gesuchten Seitenlängen kann man auch aus der Blickrichtung des Winkels α bestimmen können. Hierfür muss man den Winkel α aus der Winkelsumme eines Dreiecks, die immer 180° beträgt, bestimmen. Demzufolge ist der Winkel α = 180° ( β + γ).
3. Beispiel: In einem rechtwinkligen Dreieck ABC ist β = 90°, γ = 22° und c = 13,7 cm.
Berechne die fehlenden Seitenlängen a und b.
Je nach Aufgabe ist die Hypotenuse die Seitenlänge a, b oder c. Demzufolge variieren auch je nach Aufgabe die Katheten des rechtwinkligen Dreiecks. Wichtig hierbei ist aber, dass die trigonometrischen Beziehungen weiterhin bestehen bleiben und nur die aufgestellten Gleichungen sich dahingehend verändern, und zwar in Abhängigkeit zur jeweiligen Hypotenuse des rechtwinkligen Dreiecks. Damit man je nach Aufgabe genau weiß, wo die Hypotenuse und die Katheten sich befinden, sollte man vorab immer eine Planskizze machen.
Da hier die Hypotenuse die Seitenlänge b ist, sind a und c die Katheten des rechtwinkligen Dreiecks. Aus der Blickrichtung des Winkels γ ergeben sich hierbei folgende trigonometrische Beziehungen:
sin γ = ${\frac{\mathrm G\mathrm e\mathrm g\mathrm e\mathrm n\mathrm k\mathrm a\mathrm t\mathrm h\mathrm e\mathrm t\mathrm e }{\mathrm H\mathrm y\mathrm p\mathrm o\mathrm t\mathrm e\mathrm n\mathrm u\mathrm s\mathrm e}}$ = ${\frac{\mathrm c }{\mathrm b}}$
Diese Gleichung muss man nun nach der Seitenlänge b hin auflösen.
sin γ = ${\frac{\mathrm c }{\mathrm b}}$ | · b
sin γ · b = c | : sin γ
b = ${\frac{\mathrm c}{sin~\gamma}}$
b = ${\frac{13,7~cm }{sin~22^\circ}}$
b = 36, 6 cm (gerundet auf eine Nachkommastelle)
tan γ = ${\frac{Gegenkathete }{Ankathete}}$ = ${\frac{c }{a}}$
Diese Gleichung muss man nun nach der Seitenlänge a hin auflösen.
tan γ = ${\frac{c }{a}}$ | · a
tan γ · a = c | : tan γ
a = ${\frac{c }{tan~\gamma}}$
a = ${\frac{13,7~cm }{tan~22^\circ}}$
a = 33,9 cm (gerundet auf eine Nachkommastelle)
Hat man bei einem rechtwinkligen Dreieck jeweils zwei Seiten gegeben oder eine zweite Seite über die trigonometrischen Beziehungen bestimmt, so kann man die dritte Seite auch stets über den Satz des Pythagoras berechnen. Siehe hierzu auch das Stoffgebiet Satz des Pythagoras an.
4. Beispiel: Gegeben ist ein rechtwinkliges Dreieck mit α = 90° und den Seitenlängen a = 21 cm und c = 17 cm.
Bestimme die Größe der Winkel β und γ sowie die Seitenlänge b.
Die Hypotenuse des rechtwinkligen Dreiecks ist a. Daher sind b und c dessen Katheten. Hieraus ergeben sich folgende trigonometrische Beziehungen:
cos β = ${\frac{Ankathete}{Hypotenuse}}$ = ${\frac{c}{a}}$
Diese Gleichung muss man nun nach dem Winkel β hin auflösen.
cos β = ${\frac{c}{a}}$
cos β = ${\frac{17~cm}{21~cm}}$ | cos−1
β = 36° (gerundet auf eine ganzzahlige Gradzahl)
sin γ = ${\frac{Gegenkathete }{Hypotenuse}}$ = ${\frac{c }{a}}$
Diese Gleichung muss nun nach dem Winkel γ hin aufgelöst werden.
sin γ = ${\frac{c }{a}}$
sin γ = ${\frac{17~cm }{21~cm}}$ | sin−1
γ = 54° (gerundet auf eine ganzzahlige Gradzahl)
Hat man einen Winkel bestimmt, so kann man den noch fehlenden Winkel auch über die Winkelsumme im Dreieck bestimmen. Es gilt ja bei jedem Dreieck: α + β + γ = 180°.
Mit dem Satz des Pythagoras kann man am schnellsten die fehlende Seitenlänge b bestimmen:
a² = b² + c²
Diese Gleichung muss man nach b hin auflösen.
a² = b² + c² | – $\mathrm{c}^{2}$
$\mathrm{a}^{2}$ – $\mathrm{c}^{2}$ = $\mathrm{b}^{2}$ | √
$\sqrt{\mathrm{a}^{2} – \mathrm{c}^{2}}$ = b
b = $\sqrt{\mathrm{a}^{2} – \mathrm{c}^{2}}$
b = $\sqrt{21~cm^{2}-17~cm^{2}}$
b = 12,3 cm (gerundet auf eine Nachkommastelle)
Die gesuchte Seitenlänge b kann man auch mit einer der trigonometrischen Beziehungen bestimmen.