Kommen in Mathe vier Geraden vor, die in ganz bestimmter Beziehung zueinander stehen, so ergeben sich hieraus bestimmte Gesetzmäßigkeiten – die Strahlensätze. Bei den vier Geraden muss hierbei Folgendes gewährleistet sein: Zwei Geraden müssen sich in einem Punkt schneiden, die zwei anderen Gerade müssen parallel zueinander verlaufen und diese beiden Geraden jeweils schneiden. Liegt solch eine Konstellation von vier Geraden vor – dann kann man hieraus die sogenannten Strahlensätze ableiten. Bei den Strahlensätzen handelt es sich hierbei um Ähnlichkeitsverhältnisse zwischen Strecken, die mittels Quotientengleichungen wiedergegeben werden können.
Diese zwei Strahlensätze gibt es:
1. Strahlensatz:
$\frac{\overline{\mathrm{ZA}}}{\overline{\mathrm{ZA}^{\prime}}}$ = $\frac{\overline{\mathrm{ZA}}}{\overline{\mathrm{ZB}^{\prime}}}$ bzw:
$\frac{\overline{\mathrm{ZA}}}{\overline{\mathrm{AA}^{\prime}}}$ = $\frac{\overline{\mathrm{ZB}}}{\overline{\mathrm{BB}^{\prime}}}$
2. Strahlensatz:
$\frac{\overline{\mathrm{AB}}}{\overline{\mathrm{A}^{\prime}\mathrm{B}^{\prime}}}$ = $\frac{\overline{\mathrm{ZB}}}{\overline{\mathrm{Z}\mathrm{A}^{\prime}}}$
bzw:
$\frac{\overline{\mathrm{AB}}}{\overline{\mathrm{A}^{\prime}\mathrm{B}^{\prime}}}$ = $\frac{\overline{\mathrm{ZB}}}{\overline{\mathrm{Z}\mathrm{B}^{\prime}}}$
Aufgaben zum Mathe-Stoffgebiet Strahlensätze
1. Mathematik-Nachhilfe-Aufgabe: Erkläre aus dem 1. Strahlensatz heraus folgende Gleichungen:
a) ${\frac{\overline{ZA‘}}{\overline{ZA}}$ = ${\frac{\overline{ZB‘}}{\overline{ZB}}$
b) ${\frac{\overline{ZA}}{\overline{ZB}}$ = ${\frac{\overline{ZA‘}}{\overline{ZB‘}}$
c) ${\frac{\overline{AA‘}}{\overline{ZA}}$ = ${\frac{\overline{BB‘}}{\overline{ZB}}$
d) ${\frac{\overline{ZA}}{\overline{ZB}}$ = ${\frac{\overline{AA‘}}{\overline{BB‘}}$
e) $\overline{ZA}$ · $\overline{ZB‘}$ = $\overline{ZB}$ · $\overline{ZA‘}$
f) $\overline{ZA}$ · $\overline{BB‘}$ = $\overline{ZB}$ · $\overline{AA‘}$
2 Mathe-Nachhilfe-Aufgabe: Erkläre vom 2. Strahlensatz her alle folgenden Gleichungen.
a) ${\frac{\overline{ZA‘}}{\overline{ZA}}$ = ${\frac{\overline{A’B‘}}{\overline{AB}}$
b) ${\frac{\overline{ZA}}{\overline{AB}}$ = ${\frac{\overline{ZA‘}}{\overline{A’B‘}}$
c) ${\frac{\overline{ZB‘}}{\overline{ZB}}$ = ${\frac{\overline{A’B‘}}{\overline{AB}}$
d) ${\frac{\overline{ZB}}{\overline{AB}}$ = ${\frac{\overline{ZB‘}}{\overline{A’B‘}}$
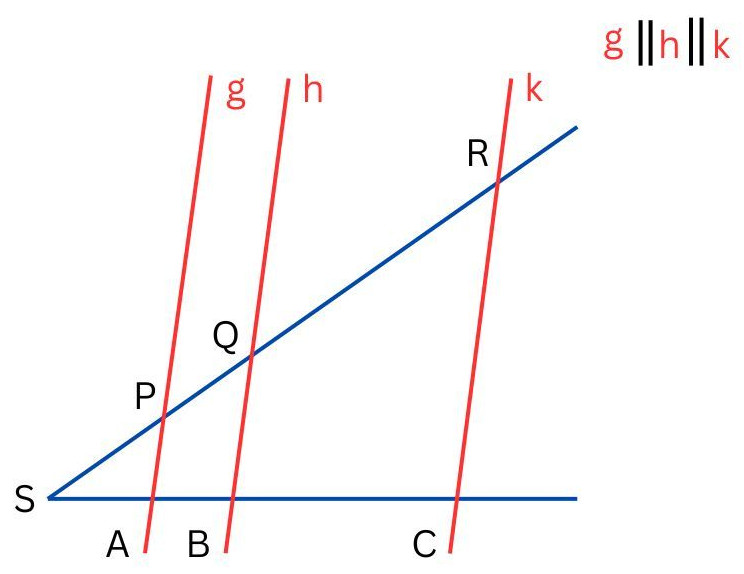
3. Mathematik-Nachhilfe-Aufgabe: Folgende Strahlensatzfigur ist gegeben. Fülle hierzu die Lücken in den Verhältnisgleichungen aus. Ziehe hierfür den 1. Strahlensatz heran. Strahlensatzfigur mit drei parallelen Strahlen
a) ${\frac{\overline{SB}}{\overline{SA}}$ = ${\frac{\framebox[4mm][r]{}}{\framebox[4mm][r]{}}$
b) ${\frac{\overline{SP}}{\overline{SR}}$ = ${\frac{\framebox[4mm][r]{}}{\framebox[4mm][r]{}}$
c) ${\frac{\overline{SC}}{\framebox[4mm][r]{}}$ = ${\frac{\framebox[4mm][r]{}}{\overline{SP}}$
d) ${\frac{\framebox[4mm][r]{}}{\overline{SQ}}$ = ${\frac{\overline{SC}}{\framebox[4mm][r]{}}$
e) ${\frac{\framebox[4mm][r]{}}{\framebox[4mm][r]{}}$ = ${\frac{\overline{SC}}{\overline{SB}}$
f) ${\frac{\framebox[4mm][r]{}}{\framebox[4mm][r]{}}$ = ${\frac{\overline{SQ}}{\overline{SP}}$
g) ${\frac{\overline{SP}}{\overline{PQ}}$ = ${\frac{\framebox[4mm][r]{}}{\framebox[4mm][r]{}}$
h) ${\frac{\overline{SQ}}{\framebox[4mm][r]{}}$ = ${\frac{\framebox[4mm][r]{}}{\overline{BC}}$
i) ${\frac{\overline{AB}}{\framebox[4mm][r]{}}$ = ${\frac{\framebox[4mm][r]{}}{\overline{SQ}}$
4. Mathematik-Nachhilfe-Aufgabe: Wende zur Ausfüllen der Lücken den 2. Strahlensatz an. Ziehe hierfür wiederum die Strahlensatzfigur aus Aufgabe 3 heran.
a) ${\frac{\overline{AP}}{\overline{BQ}}$ = ${\frac{\framebox[4mm][r]{}}{\framebox[4mm][r]{}}$
b) ${\frac{\overline{BQ}}{\overline{CR}}$ = ${\frac{\framebox[4mm][r]{}}{\framebox[4mm][r]{}}$
c) ${\frac{\overline{AP}}{\framebox[4mm][r]{}}$ = ${\frac{\framebox[4mm][r]{}}{\overline{SR}}$
d) ${\frac{\overline{SP}}{\framebox[4mm][r]{}}$ = ${\frac{\framebox[4mm][r]{}}{\overline{RC}}$
e) ${\frac{\framebox[4mm][r]{}}{\overline{SB}}$ = ${\frac{\overline{RC}}{\framebox[4mm][r]{}}$
Lösungen zum Mathe-Stoffgebiet Strahlensätze
1. Mathe-Nachhilfe-Aufgabe: Erkläre jede Gleichung mithilfe des 1. Strahlensatzes. Strahlensätze – erste Darstellung
Die erste Darstellung des Strahlensatzes sieht ja aus, wie auf dem obigen Strahlenfigur dargestellt. Hieraus kann man nun sogenannte Verhältnisgleichungen aufstellen, Gleichungen, die jeweils aus zwei Brüchen bestehen.
a) ${\frac{\overline{ZA‘}}{\overline{ZA}}$ = ${\frac{\overline{ZB‘}}{\overline{ZB}}$
Hier verhält es sich so, dass die Strecke $\overline{ZA‘}$ sich zu der Strecke $\overline{ZA}$ auf der Geraden genauso verhält wie die Strecke $\overline{ZB‘}$ zu der Strecke $\overline{ZB}$ auf der anderen Geraden. In der Sprache der Mathematik kann man das jeweils mit einem Bruch links und rechts einer Gleichung wiedergeben. Es handelt sich hier um den 1. Strahlensatz. Indem man den „doppelten“ Kehrwert hier vornimmt, erhält man die normale Schreibweise:
a) ${\frac{\overline{ZA‘}}{\overline{ZA}}$ =${\frac{\overline{ZB‘}}{\overline{ZB}}$
a) ${\frac{\overline{ZA}}{\overline{ZA‘}}$ =${\frac{\overline{ZB}}{\overline{ZB‘}}$
b) ${\frac{\overline{ZA}}{\overline{ZB}}$ =${\frac{\overline{ZA‘}}{\overline{ZB‘}}$
Hier stehen die Stecken in folgendem Verhältnis zueinander: Die Strecke $\overline{ZA}$ verhält sich zu der Strecke $\overline{ZA}$ genauso wie die Strecke $\overline{ZA‘}$ zu der Strecke $\overline{ZB‘}$. Das gilt für die beiden jeweiligen Geraden. Es handelt sich hierum wieder um den 1. Strahlensatz. Eine Umformung der Strecken belegt das eindeutig:
b) ${\frac{\overline{ZA}}{\overline{ZB}}$ = ${\frac{\overline{ZA‘}}{\overline{ZB‘}}$ | · $\overline{ZB}$
b) $\overline{ZA}$ =[latexpage] ${\frac{\overline{ZA‘}}{\overline{ZB‘}}$ · $\overline{ZB}$ | : $\overline{ZA‘}$
b) ${\frac{\overline{ZA}}{\overline{ZA‘}}$ = [latexpage] ${\frac{\overline{ZB}}{\overline{ZB‘}}$
c) ${\frac{\overline{AA‘}}{\overline{ZA}}$ = ${\frac{\overline{BB‘}}{\overline{ZB}}$
Folgende Streckenverhältnisse gelten hier für die beiden Geraden: Die Strecke $\overline{AA‘}$ verhält sich zu der Strecke $\overline{ZA}$ genauso wie die Strecke $\overline{BB‘}$ zu der Strecke $\overline{ZB}$.
Mit einem „doppelten“ Kehrwert erhält man die alternative übliche Schreibweise des 1. Strahlensatzes.
c) ${\frac{\overline{AA‘}}{\overline{ZA}}$ =${\frac{\overline{BB‘}}{\overline{ZB}}$ <=>
c) ${\frac{\overline{ZA}}{\overline{AA‘}}$ =${\frac{\overline{ZB}}{\overline{BB‘}}$
d) ${\frac{\overline{ZA}}{\overline{ZB}}$ =${\frac{\overline{AA‘}}{\overline{BB‘}}$
Die jeweiligen Strecken $\overline{ZA}$ und $\overline{ZB}$ auf den beiden Geraden verhalten sich genauso wie die beiden anderen Strecken $\overline{AA‘}$ und $\overline{BB‘}$ auf den Geraden. Hierbei handelt es sich auch um den 1. Strahlensatz. Mit einfachen Umformungen lässt sich die Verhältnisgleichung hin zu der gewohnten des 1. Strahlensatzes hin umwandeln.
d) ${\frac{\overline{ZA}}{\overline{ZB}}$ = ${\frac{\overline{AA‘}}{\overline{BB‘}}$ | · $\overline{ZB}$
d) $\overline{ZA}$ =[latexpage] ${\frac{\overline{AA‘}}{\overline{BB‘}}$ · $\overline{ZB}$ | : $\overline{AA‘}$
d) ${\frac{\overline{ZA}}{\overline{AA‘}}$ = ${\frac{\overline{ZB}}{\overline{BB‘}}$
e) $\overline{ZA}$ · $\overline{ZB‘}$ = $\overline{ZB}$ · $\overline{ZA‘}$
Hier verhält sich das Produkt der Strecken $\overline{ZA}$ und $\overline{ZB‘}$ der beiden Geraden so wie das Produkt der anderen Strecken $\overline{ZB}$ und $\overline{ZA‘}$ der Geraden. Auch hier liegt der 1. Strahlensatz vor. Mittels Umformung erhält man seine gewohnte Darstellungsform.
e) $\overline{ZA}$ · $\overline{ZB‘}$ = $\overline{ZB}$ · $\overline{ZA‘}$ | :$\overline{ZA‘}$
e) ${\frac{\overline{ZA}}{\overline{ZA‘}}$ = $\overline{ZB}$ | :$\overline{ZB‘}$
e) ${\frac{\overline{ZA}}{\overline{ZA‘}}$ = ${\frac{\overline{ZB}}{\overline{ZB‘}}$
f) $\overline{ZA}$ · $\overline{BB‘}$ = $\overline{ZB}$ · $\overline{AA‘}$
Hier verhält sich das Produkt der beiden Strecken $\overline{ZA}$ und $\overline{BB‘}$ beider Geraden gleich den Strecken $\overline{ZB}$ und $\overline{AA‘}$ der anderen beiden Geraden. Hier liegt wiederum der 1. Strahlensatz vor. Mittels Äquivalenzumformungen kann man diesen in die gewohnte Darstellung bringen.
f) $\overline{ZA}$ · $\overline{BB‘}$ = $\overline{ZB}$ · $\overline{AA‘}$ : $\overline{AA‘}$
f) ${\frac{\overline{ZA}}{\overline{AA‘}}$ · $\overline{BB‘}$ = $\overline{ZB}$ : $\overline{BB‘}$
f) ${\frac{\overline{ZA}}{\overline{AA‘}}$ = ${\frac{\overline{ZB}}{\overline{BB‘}}$
2. Mathe-Nachhilfe-Aufgabe: Die folgenden Gleichungen sollen mittels des 2. Strahlensatzes erklärt werden. Strahlensätze – zweite Darstellung
Die zweite Strahlensatzfigur sieht ja folgendermaßen aus wie auf dem obigen Bild. Hieraus kann man auch den 2. Strahlensatz in Form von Bruchgleichungen aufstellen.
a) ${\frac{\overline{ZA‘}}{\overline{ZA}}$ = ${\frac{\overline{A’B‘}}{\overline{AB}}$
Die Strecken $\overline{ZA‘}$ und $\overline{ZA}$ der Gerade verhalten sich genauso wie die Strecken $\overline{A’B‘}$ und $\overline{AB}$ der Geraden. Hier handelt sich genau um den 2. Strahlensatz in der bekannten Darstellungsweise. Hierzu muss man nur noch den „doppelten“ Kehrwert durchführen.
a) ${\frac{\overline{ZA‘}}{\overline{ZA}}$ = ${\frac{\overline{A’B‘}}{\overline{AB}}$
a) ${\frac{\overline{ZA}}{\overline{ZA‘}}$ = ${\frac{\overline{AB}}{\overline{A’B‘}}$
b) ${\frac{\overline{ZA}}{\overline{AB}}$ = ${\frac{\overline{ZA‘}}{\overline{A’B‘}}$
Hier verhalten sich die Strecken $\overline{ZA}$ und $\overline{AB}$ der Geraden genauso zu den Strecken $\overline{ZA‘}$ und $\overline{A’B‘}$. Mittels Äquivalenzumforumgen ergibt sich eindeutig die Darstellung des 2. Strahlensatzes.
b) ${\frac{\overline{ZA}}{\overline{AB}}$ = ${\frac{\overline{ZA‘}}{\overline{A’B‘}}$ | · $\overline{AB}$
b) $\overline{ZA}$ = ${\frac{\overline{ZA‘}}{\overline{A’B‘}}$ · $\overline{AB}$ | :$\overline{ZA‘}$
b) ${\frac{\overline{ZA}}{\overline{ZA‘}}$ = ${\frac{\overline{AB}}{\overline{A’B‘}}$
c) ${\frac{\overline{ZB‘}}{\overline{ZB}}$ = ${\frac{\overline{A’B‘}}{\overline{AB}}$
Hier verhalten sich die Strecken $\overline{ZB‘}$ und $\overline{ZB}$ der Geraden genauso wie die Strecken $\overline{A’B‘}$ und $\overline{AB}$ der beiden Geraden. Hier liegt ebenfalls der 2. Strahlensatz vor. Mittels eines „doppelten“ Kehrwerts erhält man seine gewohnte Darstellung.
c) ${\frac{\overline{ZB‘}}{\overline{ZB}}$ = ${\frac{\overline{A’B‘}}{\overline{AB}}$
c) ${\frac{\overline{ZB}}{\overline{ZB‘}}$ = ${\frac{\overline{AB}}{\overline{A’B‘}}$
d) ${\frac{\overline{ZB}}{\overline{AB}}$ = ${\frac{\overline{ZB‘}}{\overline{A’B‘}}$
Hier verhalten sich die Strecken $\overline{ZB}$ und $\overline{AB}$ der Geraden genauso wie die Strecken $\overline{ZB‘}$ und $\overline{A’B‘}$ der Geraden. Hier liegt ebenfalls der 2. Strahlensatz vor. Mittels Äquivalenzumformungen kann man ihn in die gewohnte Darstellung bringen.
d) ${\frac{\overline{ZB}}{\overline{AB}}$ = ${\frac{\overline{ZB‘}}{\overline{A’B‘}}$ | · $\overline{AB}$
d) $\overline{ZB}$ = ${\frac{\overline{ZB‘}}{\overline{A’B‘}}$ · $\overline{AB}$ | :$\overline{ZB‘}$ <=>
d) ${\frac{\overline{ZB}}{\overline{ZB‘}}$ = ${\frac{\overline{AB}}{\overline{A’B‘}}$
3. Mathe-Nachhilfe-Aufgabe: Anhand folgender Strahlensatzfigur sollen die Lücken der gegebenen Verhältnisgleichungen ausgefüllt werden. Hierzu muss jeweils der 1. Strahlensatz herangezogen werden. Strahlensatzfigur mit drei parallelen Strahlen
a) ${\frac{\overline{SB}}{\overline{SA}}$ = ${\frac{\framebox[4mm][r]{}}{\framebox[4mm][r]{}}$
a) ${\frac{\overline{SB}}{\overline{SA}}$ = ${\frac{\overline{SQ}}{\overline{SP}}$
b) ${\frac{\overline{SP}}{\overline{SR}}$ = ${\frac{\framebox[4mm][r]{}}{\framebox[4mm][r]{}}$
b) ${\frac{\overline{SP}}{\overline{SR}}$ = ${\frac{\overline{SA}}{\overline{SC}}$
c) ${\frac{\overline{SC}}{\framebox[4mm][r]{}}$ = ${\frac{\framebox[4mm][r]{}}{\overline{SP}}$
c) ${\frac{\overline{SC}}{\overline{SA}}$ = ${\frac{\overline{SR}}{\overline{SP}}$
d) ${\frac{\framebox[4mm][r]{}}{\overline{SQ}}$ = ${\frac{\overline{SC}}{\framebox[4mm][r]{}}$
d) ${\frac{\overline{SR}}{\overline{SQ}}$ = ${\frac{\overline{SC}}{\overline{SB}}$
e) ${\frac{\framebox[4mm][r]{}}{\framebox[4mm][r]{}}$ = ${\frac{\overline{SC}}{\overline{SB}}$
e) ${\frac{\overline{SR}}{\overline{SQ}}$ = ${\frac{\overline{SC}}{\overline{SB}}$
f) ${\frac{\framebox[4mm][r]{}}{\framebox[4mm][r]{}}$ = ${\frac{\overline{SQ}}{\overline{SP}}$
f) ${\frac{\overline{SB}}{\overline{SA}}$ = ${\frac{\overline{SQ}}{\overline{SP}}$
g) ${\frac{\overline{SP}}{\overline{PQ}}$ = ${\frac{\framebox[4mm][r]{}}{\framebox[4mm][r]{}}$
g) ${\frac{\overline{SP}}{\overline{PQ}}$ = ${\frac{\overline{SA}}{\overline{AB}}$
h) ${\frac{\overline{SQ}}{\framebox[4mm][r]{}}$ = ${\frac{\framebox[4mm][r]{}}{\overline{BC}}$
h) ${\frac{\overline{SQ}}{\overline{QR}}$ = ${\frac{\overline{SB}}{\overline{BC}}$
i) ${\frac{\overline{AB}}{\framebox[4mm][r]{}}$ = ${\frac{\framebox[4mm][r]{}}{\overline{SQ}}$
i) ${\frac{\overline{AB}}{\overline{SB}}$ = ${\frac{\overline{PQ}}{\overline{SQ}}$
4. Mathematik-Nachhilfe-Aufgabe: Fülle die Lücken mithilfe des 2. Strahlensatzes aus. Die Strahlensatzfigur aus Aufgabe 3 dient hierfür als Grundlage. Strahlensatzfigur mit drei parallelen Strahlen
a) ${\frac{\overline{AP}}{\overline{BQ}}$ = ${\frac{\framebox[4mm][r]{}}{\framebox[4mm][r]{}}$
a) ${\frac{\overline{AP}}{\overline{BQ}}$ = ${\frac{\overline{SA}}{\overline{SB}}$
oder:
a) ${\frac{\overline{AP}}{\overline{BQ}}$ = ${\frac{\overline{SP}}{\overline{SQ}}$
b) ${\frac{\overline{BQ}}{\overline{CR}}$ = ${\frac{\framebox[4mm][r]{}}{\framebox[4mm][r]{}}$
b) ${\frac{\overline{BQ}}{\overline{CR}}$ = ${\frac{\overline{SB}}{\overline{SC}}$
oder:
b) ${\frac{\overline{BQ}}{\overline{CR}}$ = ${\frac{\overline{SQ}}{\overline{SR}}$
c) ${\frac{\overline{AP}}{\framebox[4mm][r]{}}$ = ${\frac{\framebox[4mm][r]{}}{\overline{SR}}$
c) ${\frac{\overline{AP}}{\overline{CR}}$ = ${\frac{\overline{SP}}{\overline{SR}}$
d) ${\frac{\overline{SP}}{\framebox[4mm][r]{}}$ = ${\frac{\framebox[4mm][r]{}}{\overline{RC}}$
d) ${\frac{\overline{SP}}{\overline{SR}}$ = ${\frac{\overline{PA}}{\overline{RC}}$
e) ${\frac{\framebox[4mm][r]{}}{\overline{SB}}$ = ${\frac{\overline{RC}}{\framebox[4mm][r]{}}$
e) ${\frac{\overline{SC}}{\overline{SB}}$ = ${\frac{\overline{RC}}{\overline{QB}}$