1. Allgemeines zu Betragsfunktionen
Bei einer Betragsfunktion weist der Term mit der Variablen Betragsstriche auf. Deshalb heißen solche Funktionen auch Betragsfunktionen, da dies deren Charakteristikum ist. Ein weiteres Merkmal bei Betragsfunktionen ist, dass man bei ihnen immer eine sogenannte Fallunterscheidung machen muss. Das liegt in der Besonderheit des Betrags begründet. Ein Betrag darf in Mathematik nämlich niemals negativ werden. Denn bei einem Betrag handelt es sich immer um ein Streckenverhältnis, das per se immer positiv ist. Mittels einer Fallunterscheidung wird das gewährleistet.
Die einfachste Betragsfunktion ist hierbei:
f(x) = |x|.
Man sagt auch, dass f(x) = |x| eine abschnittsweise lineare Funktion ist. Denn diese Funktion ist in einem bestimmten Intervall abschnittsweise linear.
Bei der Funktion f(x) = |x| gilt folgende Fallunterscheidung, da ja der Betrag niemals negativ werden darf:
f(x) = [latexpage] $\left\{\begin{array}{rcl}\mathrm x~\mathrm{f\“ur}\in~\mathbb R^+_0&& \\\mathrm x~\mathrm{f\“ur}\in~\mathbb R^-&& \end{array}\right.$
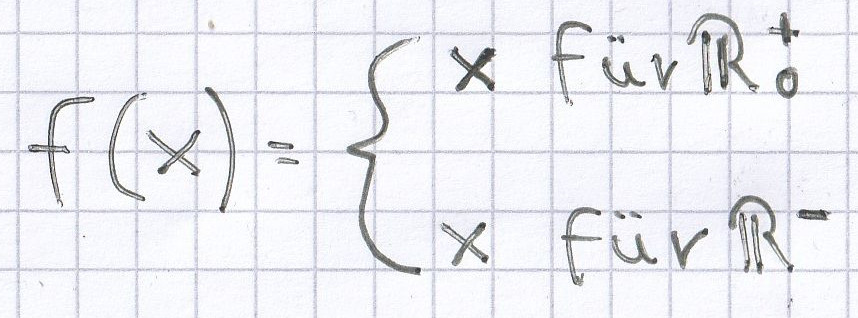
Jeder reelen Zahl wird bei dieser Funktion ihr Betrag zugeordnet.
Es gilt hierfür auch folgende Zuordnungsvorschrift: f: x ↦ |x|; x ∈ ℝ.
Die Betragsfunktion f(x) = |x| hat diesen Graphen:
Die Funktion f(x) = |x| ist nach dem Koordinatenursprung linear steigend und vor dem Koordinatenursprung linear fallend. Als Nullpunkt hat die Funktion die Koordinate N (0 | 0).
