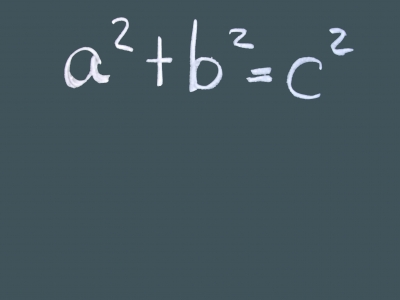
Bei einem rechtwinkligen Dreieck gilt der Satz des Pythagoras. Demzufolge gilt diese sehr berühmte Gesetzmäßigkeit nicht, wenn kein rechtwinkliges Dreieck vorliegt. Ist nun ein rechtwinkliges Dreieck gegeben, dann weist solch ein Dreieck immer eine Hypotenuse und zwei Katheten auf. Was ist aber was? Das ist ganz, ganz einfach – und sollte man deshalb auch nie vergessen. Die Hypotenuse ist immer die Seite im rechtwinkligen Dreieck, die sich gegenüber dem rechten Winkel befindet. Die anderen Seiten sind dann stets die Katheten, da die Hypotenuse ja immer festgelegt ist. Demzufolge ist auch stets klar, wenn man den Satz des Pythagoras an einem beliebigen rechtwinkligen Dreieck aufgestellt, was für eine Gleichung sich ergibt bzw. ergeben muss .