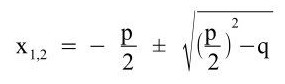Schlagwort: pq-Formel

Kategorien
Gleichungen Mathe Mathematik Nachhilfe Quadratische Gleichungen

Mathematik-Nachhilfe: Aufgaben zu quadratischen Gleichungen, Teil 4

Der beste Lösungsweg für quadratische Gleichungen hängt von der jeweiligen Gleichung ab © S. Hofschlaeger / PIXELIO

In Mathe bei quadratischen Gleichungen die Lösungsmenge mittels pq-Formel oder quadratischen Ergänzens zu bestimmen, macht nur Sinn, wenn die quadratische Gleichung alle Glieder vorweist. Konkret heißt das: Liegt eine quadratische Gleichung mit einem quadratischen Glied/„ax²“, mit einem linearen Glied/„bx“ und einem absoluten Glied/„c“ vor, dann muss man obige Lösungsverfahren anwenden. Fehlt hingegen mindestens das lineare Glied oder das absolute Glied, dann löst man die quadratische Gleichung immer anders. Auch Ökonomie ist im Fach Mathematik sehr wichtig, da dies eine nicht zu unterschätzende Zeitersparnis mit sich bringt. Je mehr Routine man aber im Lösen von quadratischen Gleichungen hat, desto mehr wird man aber auch automatisch stets das beste Lösungsverfahren, sprich das am ökonomischsten, anwenden.

Weiterlesen „Mathematik-Nachhilfe: Aufgaben zu quadratischen Gleichungen, Teil 4“
Kategorien
Gleichungen Mathe Mathematik Nachhilfe Quadratische Gleichungen

Mathematik-Nachhilfe: Aufgaben zu quadratischen Gleichungen, Teil 3

Algebra in Mathe © Henry Klingberg / PIXELIO

Liegt in Mathe eine quadratische Gleichung in der sogenannten Normalform vor, das heißt auf diese Art: x² + px + q, dann kann man sofort ohne Probleme deren Lösung(en) ermitteln. Hierfür gibt es ja extra die pq-Formel:

p-q-Formel

Schließlich kann man bei der Normalform den p-Wert und den q-Wert der quadratischen Gleichung sofort ablesen, so dass man daher im Nu mittels der p-q-Formel deren Lösung(en) berechnen kann. Jetzt gilt es die Werte nur noch richtig einzusetzen. Hier muss man aber immer darauf Acht geben, dass speziell sowohl bei einem negativen p-Wert als auch negativen q-Wert die Vorzeichenregel richtig angewendet wird. Konkret heißt das, dass „–“ und „–“ „+“ ergeben, wenn entweder beim Einsetzen in die pq-Formel der p-Wert oder der q-Wert negativ sind.

Weiterlesen „Mathematik-Nachhilfe: Aufgaben zu quadratischen Gleichungen, Teil 3“
Kategorien
Gleichungen Mathe Mathematik Nachhilfe Quadratische Gleichungen Terme

Mathematik-Nachhilfe: Aufgaben zu quadratischen Gleichungen, Teil 2

Mitternacht © Simone Hainz / PIXELIO

Wenn ehemalige Schülerinnen und Schüler zu einer ganz bestimmten späteren Uhrzeit an Mathematik denken müssen – dann hat dies meist einen bestimmten Grund: Sie erinnern sich der großen Wichtigkeit einer Formel aus ihrem damaligen Mathe-Unterreicht – und zwar an die sogenannte Mitternachtsformel. Jeder, der früher Abitur gemacht hat, musste sich nämlich von seinem Mathe-Lehrer immer wieder gebetsmühlenartig anhören: „Diese Formel ist so wichtig, dass ihr sie sogar zu Mitternacht (und natürlich auch noch zu späterer Stunde 😉 ) auswendig vorsagen können müsst (und das, egal, wie euer geistiges und körperliches Befinden zu dieser Uhrzeit gerade ist 😉 )!“ Die Ergänzungen in der Klammer sind natürlich von mir spaßeshalber hinzugefügt worden, die Aussage des Lehrers entspricht jedoch einer wortwörtlichen Wiedergabe aus dem Mathe-Unterricht der Jahrzehnte vor dem 21. Jahrhundert. Denn noch vor der Schulreform und der damit einhergehenden Reform des Mathematik-Unterrichts hatte die Mitternachtsformel, mit der man die Lösungsmenge jeder quadratischen Gleichung der Form ax² + bx + c = 0 (a, b, x ∈ von und a ≠ 0) bestimmen kann, einen extrem hohen Stellenwert. Inzwischen sieht das jedoch fundamental anders aus!

Weiterlesen „Mathematik-Nachhilfe: Aufgaben zu quadratischen Gleichungen, Teil 2“