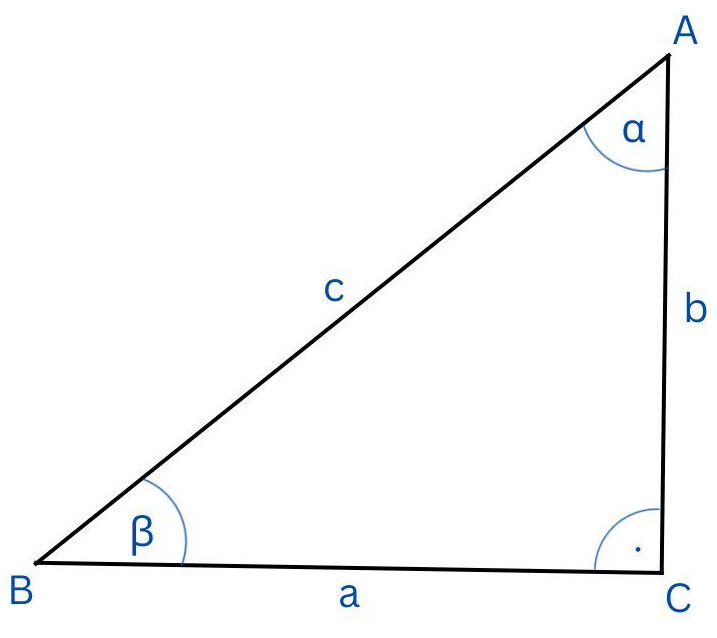
Rechtwinkliges Dreieck mit Längen- und Winkelangabe Stehen in Mathe Berechnungen am rechtwinkligen Dreieck an der Tagesordnung und man muss hierfür nicht den Satz des Pythagoras heranziehen, so hat man das Stoffgebiet Trigonometrie vor der Brust. Mithilfe der trigonometrischen Beziehungen lassen sich nämlich auch die Seiten eines rechtwinkligen Dreiecks berechnen. Im Gegensatz zu dem Satz des Pythagoras macht man das aber entweder mittels zweier Seitenlängen oderzusammen mit einem Winkel und einer Seitenlänge des Dreiecks. Aber im Prinzip ist das Stoffgebiet ähnlich schwer bzw. leicht (wenn man in Mathematik nicht gänzlich auf den Kopf gefallen ist ;-)). Man muss nur die trigonometrischen Beziehungen anwenden – und am besten auch noch auswendig können. Folgende drei trigonometrischen Beziehungen gibt es hierbei:
Vom Blickwinkel des Winkels α:
sin α = [latexpage] ${\frac{Gegenkathete }{Hypotenuse}}$ = ${\frac{a }{c}}$
cos α = [latexpage] ${\frac{Ankathete}{Hypotenuse}}$ = ${\frac{b}{c}}$
tan α = [latexpage] ${\frac{Gegenkathete}{Ankathete}}$ = ${\frac{a}{b}}$
Vom Blickwinkel des Winkels β:
sin β = [latexpage] ${\frac{Gegenkathete }{Hypotenuse}}$ = ${\frac{b }{c}}$
cos β = [latexpage] ${\frac{Ankathete}{Hypotenuse}}$ = ${\frac{a}{c}}$
tan β = [latexpage] ${\frac{Gegenkathete}{Ankathete}}$ = ${\frac{b}{a}}$
Aufgaben zum Mathe-Stoffgebiet Trigonometrie am rechtwinkligen Dreieck
1. Mathe-Nachhilfe-Aufgabe: In einem Dreieck ABC mit α = 90° sind folgende Seitenlängen gegeben:
a) a = 14,1 cm b) a = 12,7 cm c) a = 29,3 cm d) a = 5,3 cm
b = 7,8 cm b = 5,9 cm b = 25,6 cm c = 3,7 cm
Berechne jeweils die fehlende Seitenlänge sowie die beiden anderen Winkel.
2. Mathematik-Nachhilfe-Aufgabe: In einem Dreieck ABC ist Folgendes gegeben:
a) a = 7,8 cm b) b = 23 cm c) a = 12,3 cm d) a = 4,3 cm
b = 5,2 cm c = 16 cm c = 9,4 cm b = 5,7 cm
γ = 90° α = 90° β = 90° γ = 90°
3. Mathe-Nachhilfe-Aufgabe: Auf Straßenkarten findet man bei Passstraßen immer die Angabe der höchsten Steigung vor. So steht da beispielsweise:
St. Gotthard: 10 %; Jaufenpass: 12 %; Furkapass: 11 %, Timmelsjoch: 13 %
a) Wie hoch ist jeweils der Steigungswinkel?
b) Welcher Höhenunterschied besteht, wenn die hierbei zurückgelegte Strecke 1,2 km beträgt?
4. Mathe-Nachhilfe-Aufgabe: In folgenden beiden Dreieck soll jeweils die rot markierte Größe berechnet werden.
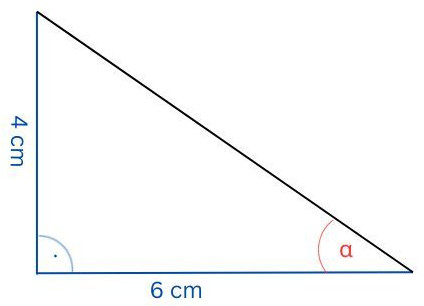
a) Ein rechtwinkliges Dreieck mit zwei Seitenangaben
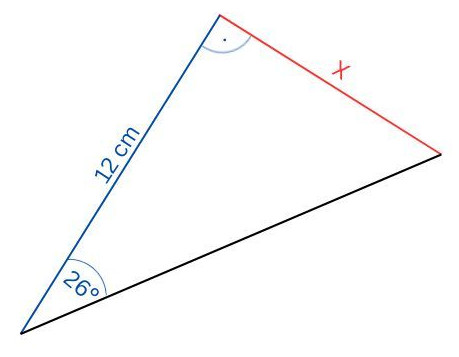
b) Ein rechtwinkliges Dreieck mit Winkel- und Seitenangabe
Lösungen zum Mathe-Stoffgebiet Trigonometrie am rechtwinkligen Dreieck
1. Mathe-Nachhilfe-Aufgabe: In einem Dreieck ABC ist der Winkel α = 90°. Darüber hinaus sind folgende Angaben gegeben:
a) a = 14,1 cm b) a = 12,7 cm c) a = 29,3 cm d) a = 5,3 cm
b = 7,8 cm b = 5,9 cm b = 25,6 cm c = 3,7 cm
Ermittle jeweils die fehlende Seitenlänge und die fehlenden Winkel.
Bevor man mit den Berechnungen beginnt, sollte man sich eine Skizze des gegebenen Dreiecks machen. Dadurch kann man nämlich viel leichter die trigonometrischen Beziehungen aufstellen. Skizze rechtwinkliges Dreieck
a) a = 14,1 cm
b = 7,8 cm
Da der Winkel α = 90° ist, ist die Seitenlänge a die Hypotenuse des Dreiecks. Denn die gegenüberliegende Seite vom rechten Winkel ist immer die Hypotenuse. Daher sind b und c die beiden Katheten des Dreiecks.
Über sin β kann man daher sofort den Winkel β bestimmen.
Denn hier gilt: sin β = [latexpage] ${\frac{Gegenkathete }{Hypotenuse}}$ = ${\frac{b }{a}}$
sin β = ${\frac{b }{a}}$ <=>
sin β = ${\frac{7,8cm}{14,1cm}}$ Ι sin – 1 <=>
β = 34° (gerundet auf eine ganzzahlige Gradzahl)
Mathematik-Nachhilfe-Hinweis: Denke daran, dass die die trigonometrischen Beziehungen immer vom Blickwinkel des jeweiligen Winkels (der nicht die Hypotenuse ist) aufgestellt werden müssen. Dadurch verändert sich auch die Gegenkathete und die Ankathete. Nur die Hypotenuse bleibt immer gleich. Siehe hierzu auch unter Trigonometrie, Am rechtwinkligen Dreieck, den 1. Punkt Die trigonometrischen Beziehungen am rechtwinkligen Dreieck an.
Den fehlenden Winkel γ kann man jetzt problemlos über die Winkelsumme eines Dreiecks berechnen. Hier gilt ja: α + β + γ = 180°.
Daher ist γ = 180° – (α + β)
γ = 180° – (90° + 34°) = 56°
Mathe-Nachhilfe-Hinweis: Den Winkel γ hätte man auch über die trigonometrische Beziehung cos γ = ${\frac{b }{a}}$ berechnen können. Über die Winkelsumme in einem Dreieck geht das aber viel, viel schneller.
Die fehlende Seite c kann man nun folgendermaßen berechnen:
cos β = ${\frac{c}{a}}$ Ι · a <=>
cos β · a = c <=>
c = cos β · a <=>
c = cos 34° · 14,1 cm <=>
c = 11,7 cm (gerundet auf eine Nachkommastelle)
Mathematik-Nachhilfe-Hinweis: Die Seite c hätte man auch folgendermaßen berechnen können: sin γ = ${\frac{c}{a}}$.
b) a = 12,7 cm
b = 5,9 cm
sin β = ${\frac{b }{a}}$ <=>
sin β = ${\frac{5,9cm}{12,7cm}}$ Ι sin – 1 <=>
β = 28° (gerundet auf eine ganzzahlige Gradzahl)
γ = 180° – (90° + 28°) = 62°
cos β = ${\frac{c}{a}}$ Ι · a <=>
cos β · a = c <=>
c = cos β · a <=>
c = cos 28° · 12,7 cm <=>
c = 11,2 cm (gerundet auf eine Nachkommastelle)
Mathe-Nachhilfe-Hinweis: Die fehlende Seite hätte man zudem auch über den Satz des Pythagoras berechnen können. Siehe hierzu auch unter Satz des Pythagoras den 2. Punkt Separieren und Auflösen der Flächenquadrate an.
c) a = 29,3 cm
b = 25,6 cm
sin β = ${\frac{b }{a}}$ <=>
sin β = ${\frac{25,6cm}{29,3cm}}$ Ι sin – 1 <=>
β = 61° (gerundet auf eine ganzzahlige Gradzahl)
γ = 180° – (90° + 61°) = 29°
cos β = ${\frac{c}{a}}$ Ι · a <=>
cos β · a = c <=>
c = cos β · a <=>
c = cos 61° · 29,3 cm <=>
c = 14,2 cm (gerundet auf eine Nachkommastelle)
d) a = 5,3 cm
c = 3,7
cos β = ${\frac{c }{a}}$ <=>
cos β = ${\frac{3,7cm}{5,3cm}}$ Ι cos – 1 <=>
β = 46° (gerundet auf eine ganzzahlige Gradzahl)
γ = 180° – (90° + 46°) = 44°
sin β = ${\frac{b}{a}}$ Ι · a <=>
sin β · a = b <=>
b = sin β · a <=>
b = sin 46° · 5,3 cm <=>
b = 3,8 cm (gerundet auf eine Nachkommastelle)
2. Mathematik-Nachhilfe-Aufgabe: Berechne die fehlenden Größen in folgenden rechtwinkligen Dreiecken.
a) a = 7,8 cm b) b = 23 cm c) a = 12,3 cm d) a = 4,3 cm
b = 5,2 cm c = 16 cm c = 9,4 cm b = 5,7 cm
γ = 90° α = 90° β = 90° γ = 90°
a) a = 7,8 cm
b = 5,2 cm
γ = 90°
Da hier γ = 90° ist, ist hier die Hypotenuse c. Daher sind die beiden Katheten geben.
Für α gilt daher:
tan α = ${\frac{a}{b}}$ <=>
tan α = ${\frac{7,8cm}{5,2cm}}$ Ι tan – 1 <=>
α = 56° (gerundet auf eine ganzzahlige Gradzahl)
β = 180° – (90° + 56°) = 34°
sin α = ${\frac{a}{c}}$ Ι · c <=>
sin α · c = a Ι : sin α <=>
c = ${\frac{a }{sin\alpha}}$ <=>
c = ${\frac{7,8cm}{sin 56^\circ}$ <=>
c = 9,4 cm (gerundet auf eine Nachkommastelle)
b) b = 23 cm
c = 16 cm
α = 90°
Da hier α = 90° ist, ist hier die Seitenlänge a die Hypotenuse. Die Seitenlängen b und c sind daher hier die Katheten.
Für β gilt daher:
tan β = ${\frac{b}{c}}$ <=>
tan β = ${\frac{23cm}{16cm}}$ Ι tan – 1 <=>
β = 55° (gerundet auf eine ganzzahlige Gradzahl)
γ = 180° – (90° + 55°) = 35°
sin β = ${\frac{b}{a}}$ Ι · a <=>
sin β · a = b Ι : sin β <=>
a = ${\frac{b }{sin\beta}}$ <=>
a = ${\frac{23cm}{sin 55^\circ}$ <=>
a = 28,1 cm (gerundet auf eine Nachkommastelle)
c) a = 12,3 cm
c = 9,4 cm
β = 90°
Da der rechte Winkel bei β ist, ist die Hypotenuse die Seitenlänge b. Die Seitenlängen a und c sind daher die Katheten.
Für α gilt daher:
tan α = ${\frac{a}{c}}$ <=>
tan α = ${\frac{12,3cm}{9,4cm}}$ Ι tan – 1 <=>
α = 53° (gerundet auf eine ganzzahlige Gradzahl)
γ = 180° – (90° + 53°) = 37°
sin α = ${\frac{a}{b}}$ Ι · b <=>
sin α · b = a Ι : sin α <=>
b = ${\frac{a }{sin\alpha}}$ <=>
b = ${\frac{12,3cm}{sin 53^\circ}$ <=>
b = 15,4 cm (gerundet auf eine Nachkommastelle)
d) a = 4,3 cm
b = 5,7 cm
γ = 90°
Der Winkel γ ist hier = 90°. Daher ist die Seitenlänge c die Hypotenuse und die Seitenlängen a und b die Katheten.
Für den Winkel α gilt daher:
tan α = ${\frac{a}{b}}$ <=>
tan α = ${\frac{4,3cm}{5,7cm}}$ Ι tan – 1 <=>
α = 37° (gerundet auf eine ganzzahlige Gradzahl)
β = 180° – (90° + 37°) = 53°
sin α = ${\frac{a}{c}}$ Ι · c <=>
sin α · c = a Ι : sin α <=>
c = ${\frac{a }{sin\alpha}}$ <=>
c = ${\frac{4,3cm}{sin 37^\circ}$ <=>
c = 7,1 cm (gerundet auf eine Nachkommastelle)
3. Mathe-Nachhilfe-Aufgabe: Die höchste Steigung auf Passstraßen.
St. Gotthard: 10 %; Jaufenpass: 12 %; Furkapass: 11 %, Timmelsjoch: 13 %
a) Gebe jeweils den Steigungswinkel an
b) Gebe den Höhenunterschied an, wenn die zurückgelegte Strecke 1,2 km einnimmt.
Die Steigung auf Straßenschildern besagt immer, dass über eine Länge von 100 m in der Waagrechten, die Höhe um so und so viel Metern zunimmt in der Senkrechten. Von den trigonometrischen Beziehungen her liegt daher immer der Tangens vor, mit dem man den Steigungswinkel berechnen kann. Nun muss man nur noch den Prozentwert in den Wert des Winkelverhältnisses von Gegenkathete durch Ankathete bringen. Das ist aber sehr leicht. 5 % Steigung sind nichts anderes als ${\frac{5}{100}}$ = 0,05 vom Tangens der trigonometrischen Beziehungen aus betrachtet. Also tan α = 0,05. Daraus ergeben sich folgende Steigungswinkel.
a) für den St. Gotthard:
tan α = ${\frac{10}{100}}$ = 0,1 Ι tan – 1 <=>
α = 5,7° (gerundet auf eine Nachkommastelle)
a) für Jaufenpass: 12 %:
tan α = ${\frac{12}{100}}$ = 0,12 Ι tan – 1 <=>
α = 6,8° (gerundet auf eine Nachkommastelle)
a) für den Furkapass: 11 %:
tan α = ${\frac{11}{100}}$ = 0,11 Ι tan – 1 <=>
α = 6,3° (gerundet auf eine Nachkommastelle)
a) für den Timmelsjoch: 13 %
tan α = ${\frac{13}{100}}$ = 0,13 Ι tan – 1 <=>
α = 7,4° (gerundet auf eine Nachkommastelle)
b) Der Höhenunterschied bei allen Passstraßen bei einer zurückgelegten Strecke von 1,2 km, berechnet man über folgende trigonometrische Beziehung:
sind α = ${\frac{Gegenkathete}{Hypotenuse}}$ = ${\frac{Höhenunterschied}{Stecke}}$ Ι · Stecke <=>
sind α · Strecke = Höhenunterschied Ι : sin α <=>
Höhenunterschied = sind α · Strecke
Die Kilometer sollte man hierbei noch in Meter umrechnen. 1 km entsprechen hierbei 1000 m.
Mathe-Nachhilfe-Hinweis: Siehe zum Umrechnen von Kilometer in Meter auch unter Größen, Das Stoffgebiet Das Umrechnen von Größen an
Daraus ergibt sich für die verschiedenen Passstraßen folgender Höhenunterschied:
b) St. Gotthard:
Höhenunterschied = sind α · Strecke = sin 5,7° · 1200 m = 119,18 m (gerundet auf zwei Nachkommastellen)
b) Jaufenpass:
Höhenunterschied = sind α · Strecke = sin 6,8° · 1200 m = 142,08 m (gerundet auf zwei Nachkommastellen)
b) Furkapass:
Höhenunterschied = sind α · Strecke = sin 6,3° · 1200 m = 131,68 m (gerundet auf zwei Nachkommastellen)
b) Timmelsjoch:
Höhenunterschied = sind α · Strecke = sin 7,4° · 1200 m = 154,55 m (gerundet auf zwei Nachkommastellen)
4. Mathematik-Nachhilfe-Aufgabe: Ermittle bei den folgenden Dreiecken die rot markierte Stelle.
a) Ein rechtwinkliges Dreieck mit zwei Seitenangaben
Der Winkel α ist hier gesucht. Die Seitenlängen der beide Katheten sind hier gegeben. Dadurch ergibt sich für den Winkel α:
tan α = ${\frac{4cm}{6cm}}$ Ι tan – 1 <=>
α = 34° (gerundet auf eine ganzzahlige Gradzahl)
b) Ein rechtwinkliges Dreieck mit Winkel- und Seitenangabe
Hier ist eine eine der beiden Katheten gesucht, die andere Kathete ist gegeben sowie ein Winkel. Für die Kathete ergibt sich:
tan 26° = ${\frac{x}{12cm}}$ Ι · 12 cm <=>
tan 26° · 12 cm = x <=>
x = tan 26° · 12 cm <=>
x = 5,85 cm (gerundet auf zwei Nachkommastellen)