
Bei der Berechnung von Flächen (dem Flächeninhalt) bei Vielecken muss man immer auf zwei Aspekte besonders Acht geben. Der erste und wichtigste Aspekt hierbei ist: die Formel zur Berechnung des Flächeninhalts eines Vielecks korrekt anzuwenden. Konkret heißt das beispielsweise: bei einem Dreieck, einem Parallelgramm oder einem Trapez die Werte korrekt in die Gleichung einzutragen. Der zweite wichtige Aspekt hierbei ist: Bevor man die Werte in die Flächeninhalts-Formel einträgt, muss man diese eventuell ALLE auf die gleiche Einheit bringen/umrechnen. Konkret heißt das, dass alle Größen beispielsweise die Einheit cm oder m vorweisen. Eigentlich ist die Berechnung eines Flächeninhalts in Mathe nicht schwer. Dennoch bleibt es ein Mathematik-Stoffgebiet – und deshalb treten hier auch immer (vor allem bei diesen beiden genannten Aspekten) Fehler auf!
Aufgaben zum Mathe-Stoffgebiet: der Flächeninhalt von Vielecken
1. Mathematik-Nachhilfe-Aufgabe: Wandle die Einheit jeweils in die nächstkleinere Einheit um.
a) 0,74 ha
b) 6,64 a
c) 32,08 km²
d) 55,87 m²
e) 6,98 ha
f) 0,04 dm²
g) 25,54 km²
h) 5,07 cm²
2. Mathe-Nachhilfe-Aufgabe: Ein Teppich auf dem Boden hat die Länge 1,80 m und die Breite 70 cm.
a) Wie kann man den Flächeninhalt des Teppichs berechnen?
b) Berechne den Flächeninhalt auf zwei Arten (in m² und in cm²)
c) Berechne den Umfang des Teppichs
3. Mathematik-Nachhilfe-Aufgabe: Ein Parallelogramm ABCD soll in ein Koordinatensystem eingezeichnet werden (Einheit 1 cm, waagrecht und senkrecht). Der Flächeninhalt des Parallelogramms soll anschließend berechnet werden, ohne dass man die Längen des Parallelogramms abmisst.
A (3 | 6)
B (1 | 2)
C (5 | 2)
D (7 | 6)
4. Mathe-Nachhilfe-Aufgabe: Ermittle die fehlende Größes des Trapezes
a) Seitenlänge a: 3,6 cm
Seitenlänge c: 2,4 cm
Höhe h: 6 cm
Flächeninhalt AT: ?
b) Seitenlänge a: 4 cm
Seitenlänge c: 10 cm
Höhe h: ?
Flächeninhalt AT: 112 cm²
c) Seitenlänge a: 7 cm
Seitenlänge c: ?
Höhe h: 6 cm
Flächeninhalt AT: 60 cm²
Lösungen zum Mathematik-Stoffgebiet: der Flächeninhalt bei Vielecken
1. Mathe-Nachhilfe-Aufgabe: Die Einheit soll jeweils in die nächstkleinere Einheit hin umgewandelt werden.
a)
0,74 ha
0,74 ha (mal 100) = 74 a
Siehe hierzu auch ergänzend unter dem Reiter Umrechnen von Größen die dort gemachten Ausführungen an.
b)
6,64 a
6,64 a (mal 100) = 664 m²
c) 32,08 km²
32,08 km² (mal 100) = 3208 ha
d)
55,87 m²
55,87 m² (mal 100) = 5587 dm²
e)
6,98 ha
6,98 ha (mal 100) = 698 a
f)
0,04 dm²
0,04 dm² (mal 100) = 4 cm²
g)
25,54 km²
25,54 km² (mal 100) = 2554 ha
h) 5,07 cm²
5,07 cm² (mal 100) = 507 mm²
2. Mathematik-Nachhilfe-Aufgabe: Auf einem Boden liegt ein Teppich mit der Länge 1,8 m und der Breite 70 cm.
a) Auf welche Weise kann man den Flächeninhalt des Teppichs berechnen?
b) Der Flächeninhalt des Teppichs soll auf zwei Arten berechnet werden (in m² und cm²).
c) Der Umfang des Teppichs soll berechnet werden.
a) Bei dem Teppich handelt es sich um ein Rechteck. Den Flächeninhalt eines Rechtecks kann man immer wie folgt berechnen:
AR = a · b
Der Flächenihalt eines Rechtecks ist Länge mal Breite.
Siehe hierzu auch unter dem Reiter Flächeninhalt 3. Flächeninhalt bei einem Rechteck ergänzend an.
b) Um den Flächeninhalt in m² oder in cm² berechnen zu können, muss man jeweils eine der beiden Größen umrechnen.
Der Flächeninhalt in m²:
b = 70 cm (durch 10 = 7 dm durch 10) = 0,7 m
AR = 1,8 m · 0,7 m
AR = 1,26 m²
Der Flächeninhalt in cm²:
a = 1,8 m (mal 10 = 18 dm mal 10) = 180 cm
AR = 180 cm · 70 cm
AR = 12600 cm²
c) Der Umfang des Teppichs setzt sich bei einem Rechteck immer folgendermaßen zusammen:
UR = a + a + b + b
UR = 2a + 2b
UR = 2 · 1,8 m + 2 · 0,7 m
UR = 3,6 m + 1,4 m
UR = 5 m
3 Mathe-Nachhilfe-Aufgabe: Es soll ein Parallelogramm ABCD in ein Koordinatensystem eingezeichnet werden (Einheit in cm, 1 cm waagrecht, ein cm senkrecht). Anschließend soll der Flächeninhalt des Parallelogramms berechnet werden, aber ohne die Strecken abzumessen.
A (3 | 6)
B (1 | 2)
C (5 | 2)
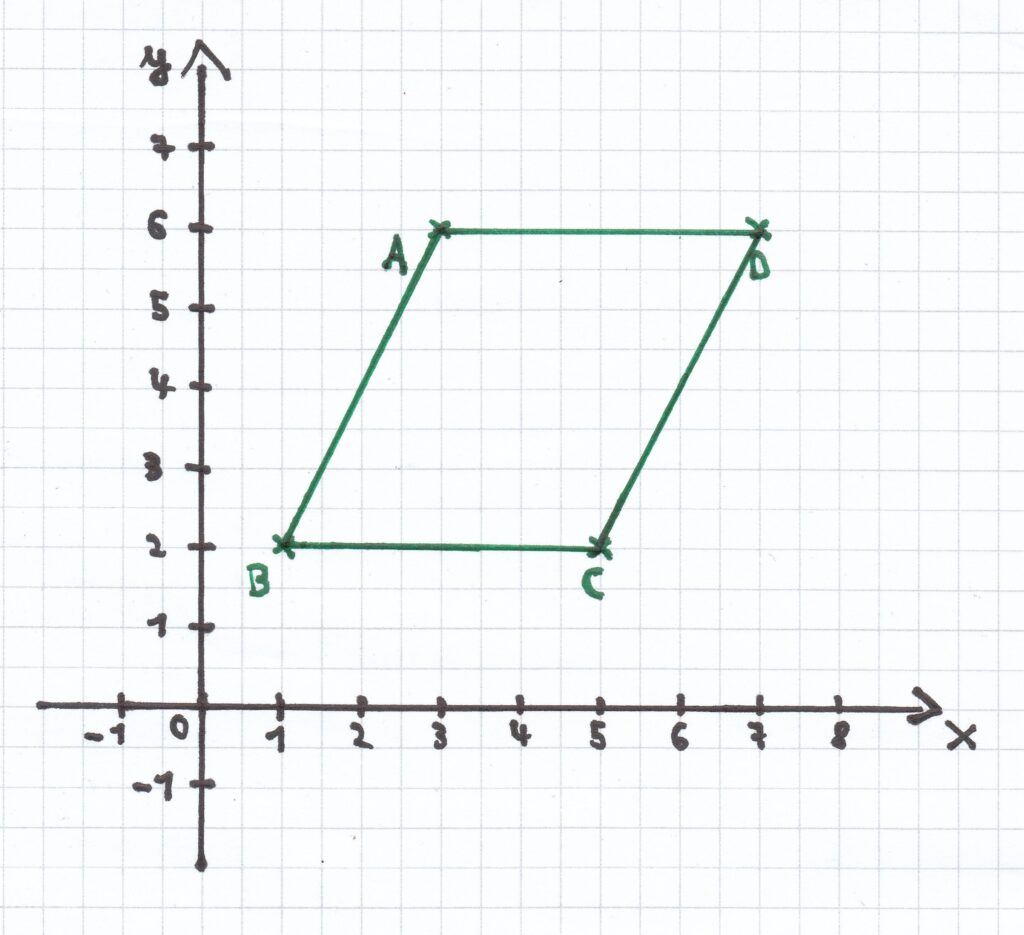
Den Flächeninhalt eines Parallelogramms berechnet man wie folgt:
AP = g · h
Auf das Parallelogramm im Koordinatensystem bezogen, entspricht g der Strecke BC/ $\overline{\mathrm B\mathrm C}$ und h entspricht der Höhe des Parallelogramms.
Aus dem eingezeichneten Parallelogramm kann man jeweils $\overline{\mathrm B\mathrm C}$ und h berechnen.
Hierbei muss man bei $\overline{\mathrm B\mathrm C}$ die beiden x-Koordinaten der Punkte C und B voneinander abziehen:
$\overline{\mathrm B\mathrm C}$ = 5 cm – 1 cm
$\overline{\mathrm B\mathrm C}$ = 4 cm
Darüber hinaus muss man für h die y-Koordinaten von A und B oder D und C voneinander abziehen:
h = 6 cm – 2 cm
h = 4 cm
Jetzt kann man den Flächeninhalt des Parallelogramms berechnen:
AP = g · h
AP = 4 cm · 4 cm
AP = 16 cm²
4. Mathematik-Nachhilfe-Aufgabe: Berechne jeweils die fehlende Größe bei einem Trapez.
a)
Seitenlänge a: 3,6 cm
Seitenlänge c: 2,4 cm
Höhe h: 6 cm
Flächeninhalt AT: ?
Hier ist der Flächeinhalt des Trapezes gesucht. Dieser berechnet sich wie folgt:
AT = ${\frac{1}{2}}$ · (a + c) · h
AT = ${\frac{1}{2}}$ · (3,6 cm + 2,4 cm) · 6cm
AT = 18 cm²
b)
Seitenlänge a: 4 cm
Seitenlänge c: 10 cm
Höhe h: ?
Flächeninhalt AT: 112 cm²
Hier ist die Höhe h des Trapezes gesucht. Die Formel muss man daher zunächst nach der Höhe h hin umformen.
AT = ${\frac{1}{2}}$ · (a + c) · h | · 2
AT · 2 = (a + c) · h | : (a + c)
h = ${\frac{\mathrm A_{\mathrm T}\ {\cdot}~2}{\mathrm a~+~\mathrm c}}$
h = ${\frac{112~\mathrm c\mathrm m^2\ {\cdot}~2}{4~\mathrm c\mathrm m~+~10~\mathrm c\mathrm m}}$
h = 16 cm
c)
Seitenlänge a: 7 cm
Seitenlänge c: ?
Höhe h: 6 cm
Flächeninhalt AT: 60 cm²
Hier ist die die Seitenlänge c des Trapezes gesucht. Hier muss man ebenfalls zunächst die Formel nach der Seitenlänge c hin umformen.
AT = ${\frac{1}{2}}$ · (a + c) · h | · 2
AT · 2 = (a + c) · h | : h
${\frac{\mathrm A_{\mathrm T}\ {\cdot}~2}{\mathrm h}}$ = a + c | – a
c = ${\frac{\mathrm A_{\mathrm T}\ {\cdot}~2}{\mathrm h}}$ – a
c = ${\frac{60~\mathrm c\mathrm m^2\ {\cdot}~2}{6~\mathrm c\mathrm m}}$ – 7 cm
c = 13 cm