Schlagwort: Potenz

Kategorien
Mathe Mathematik Nachhilfe Potenzen Rechenoperationen

Mathematik-Nachhilfe: Aufgaben zu Potenzen, Teil 9

Der Sinn des Lernens © Dieter Schütz / PIXELIO

Nach dem MSA oder dem Abitur hat man oftmals nur noch begrenzt etwas mit Mathe zu tun. Fast alles, was man im Fach Mathematik lernen musste, ist nicht wirklich alltagskompatibel. Das ist aber auch nicht weiter schlimm. Es geht ja auch nicht um die spätere konkrete Anwendung von dem, was man in der Schule lernt – sondern um das Verstehen! Hat man die durchlaufenden Stoffgebiete in Mathe beispielsweise gut VERSTANDEN, so hat man eine anspruchsvolle Geistesleistung vollbracht. Und das ist viel wert. Denn jede Geistesleistung bringt einen im Leben weiter! Das Gleiche gilt natürlich für körperlich vollbrachte Leistungen! Aus diesem Grund ist das, was man im Fach Mathe lernt, alles andere als unwichtig – ebenso das, was man in allen anderen Fächern lernt. Nur so entwickelt man sich POTENT weiter – sein ganzes Leben lang.

Weiterlesen „Mathematik-Nachhilfe: Aufgaben zu Potenzen, Teil 9“
Kategorien
Mathe Mathematik Nachhilfe Potenzen Rechenoperationen

Mathematik-Nachhilfe: Aufgaben zu Potenzen, Teil 8

Mathe-Nachhilfe in Potenzen und anderen Stoffgebieten © bschpic / PIXELIO

Vielen Schülerinnen und Schülern wird oft Angst und Bange, wenn diese die Mathe-Arbeit zu dem Thema Potenzen zurückbekommen. Spätestens wenn der Mathematik-Lehrer sagt: „Der Durchschnitt der Arbeit liegt bei 3,4“, ist bei einem im Unterricht das eigene Nervenkostüm sehr angespannt. Das sehr ungute Gefühl, das man bereits kurz nach der Arbeit hatte, hat sich nun offenbar bewahrheitet. Und die Note 5 oder gar eine 6 ist ja auch alles andere als schön, wenn man solch eine Note tatsächlich schließlich erhält. In einem Hauptfach wie Mathe verursacht diese sofort Versetzungspanik. Viele Eltern schicken daher – so meine Erfahrung – dann ihre Filia oder ihren Filius zur Nachhilfe. In der Regel ist aber nur jene eine Arbeit mörderverhauen worden – und daher eine Mathe-Nachhilfe totaler Quatsch! Die Ursache für das Komplettversagen liegt einfach an der unzureichenden Verinnerlichung der neuen Potenz-Algebra-Materie – und die muss man einfach pauken!

Weiterlesen „Mathematik-Nachhilfe: Aufgaben zu Potenzen, Teil 8“
Kategorien
Gleichungen Mathe Mathematik Nachhilfe Quadratische Gleichungen

Mathematik Nachhilfe: Aufgaben zu quadratischen Gleichungen, Teil 8

Der falsche Mathe-Lösungsweg © Tim Reckmann / PIXELIO

Liegt eine reinquadratische Gleichung vor, so kann man diese natürlich auch über die Anwendung der p-q-Formel lösen! Das geht natürlich – das ist aber alles andere als logisch sinnvoll! In Mathe geht es ja auch beim Aufgabenlösen um den möglichst unkompliziertesten und damit auch schnellsten Weg. Neben einer Zeitersparnis ist dieser Weg auch immer mit einem Fehlerverringerungsrisiko verbunden. Ein Musterbeispiel stellt hierfür eine reinquadratische Gleichung dar. Da diese keinen Mittelterm aufweist, kann diese im Nu durch ein Wurzelziehen gelöst werden. Mit der p-q-Formel geht das, wie gesagt, auch, das dauert aber viel, viel länger. Auch besteht hierbei die Gefahr, dass man einen Leichtsinnsfehler macht – und wirklich unnötige und somit wirklich ärgerliche Punkte verliert. Das spiegelt sich ja wiederum in der Mathe-Note wider!

Weiterlesen „Mathematik Nachhilfe: Aufgaben zu quadratischen Gleichungen, Teil 8“
Kategorien
Mathe Mathematik Nachhilfe Potenzen Rechenoperationen

Mathematik-Nachhilfe: Aufgaben zu Potenzen, Teil 7

Formel zur Berechnung der Fliehkraft © Karl-Heinz Laube / PIXELIO

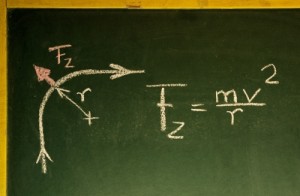
Hört das denn mit Potenzen niemals auf in Mathe? Die Antwort lautet ganz klar: nein! Solange man in die Schule geht, werden Potenzen einem im Fach Mathematik immer wieder begegnen. Daher stellen auch die Potenzgesetze ein Fundamentalwissen dar. Hat man dieses Fudamentalwissen nicht, dann kann man sehr leicht ableiten, dass einem die Vereinfachung von Termen mittels algebraischer Umformungen sicherlich äußerst schwerfällt. Und das ist nur sozusagen das Handwerkszeug, das man flink abspulen können sollte. Die eigentliche Mathematik-Problemstellung stellt normalerweise ja noch die viel größere zu bewältigende Schwierigkeit dar. Wie man sieht, können Potenzen in Mathe fiese Fallstricke sein – und das gilt dann oft für die komplette zu lösende Aufgabe.

Weiterlesen „Mathematik-Nachhilfe: Aufgaben zu Potenzen, Teil 7“
Kategorien
Mathe Mathematik Nachhilfe Terme

Mathematik-Nachhilfe: Aufgaben zu Wurzeln, Teil 4

Ein „schreckliches“ Tafelbild aus dem Mathematik-Unterricht © bernhard / PIXELIO

Terme, die einem in Mathe Angst machen, sind ein Ausdruck von algebraischer Unsicherheit. Je schwieriger die Terme werden, desto stärker kann daher auch die Verunsicherung steigen – und somit auch der Frust. Das kann einem dann im Nu das ganze Fach Mathematik verleiden. So weit sollte es daher unter keinen Umständen kommen! Terme sollten für einen keine Term-Monster werden. Oft bekommen Schülerinnen und Schüler größere algebraische Schwierigkeiten bei ganz neu aussehenden Term-Gebilden, wie das bei Wurzeln der Fall ist. Das Wurzelzeichen stellt ja auch ein ganz neues und deshalb erst einmal ein gänzlich ungewohntes Zeichen dar. Bei Wurzeln gilt aber das Gleiche wie bei anderen Term-Ausdrücken: Sie verlieren ihren Schrecken – durch Üben, Üben, Üben anhand von Aufgaben.

Weiterlesen „Mathematik-Nachhilfe: Aufgaben zu Wurzeln, Teil 4“