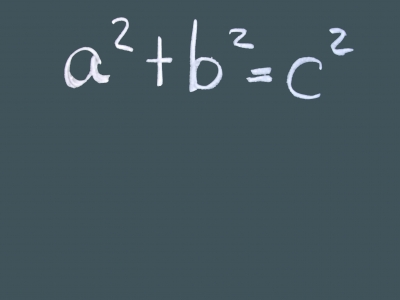Kategorie: Mathematik

Kategorien
Mathe Mathematik Nachhilfe Potenzen Rechenoperationen

Mathematik-Nachhilfe: Aufgaben zu Potenzen, Teil 10

Schwierig hoch 12 © Rainer Sturm / PIXELIO

Auch im Alltag benutzt man in seinem aktiven Wortschatz Potenzen. Das ist immer der Fall, wenn man etwas sehr Schwieriges oder eine – sagen wir mal auch in Anführungszeichen – sehr schwierige Person vor sich hat. „Die Aufgabe, die ich zu bewältigen habe, ist kompliziert hoch zwölf“, sagt ein Schüler zu einem anderen. „Die Person, mit der ich zusammenarbeiten muss, nervt mich im Quadrat“, antwortet eine Frau gegenüber ihrem Freund. Diese Aufgabe oder Person ist natürlich nicht an sich in der jeweiligen Potenz so schwierig bzw. schlimm. Dennoch empfindet ein Mensch das so – was natürlich dennoch real eine sehr schwierige Situation für diese Person ist. Am besten man ist selbst potent genug, um solche immer wieder im Leben auftretenden Situationen so gut wie möglich zu meistern.

Weiterlesen „Mathematik-Nachhilfe: Aufgaben zu Potenzen, Teil 10“
Kategorien
Bruchterme Gleichungen Mathe Mathematik Nachhilfe

Mathematik-Nachhilfe: Aufgaben zu Bruchtermen, Teil 10

Bruchterme sind super © Esther Stosch / PIXELIO

Alle Aufgaben in Mathe zu Bruchtermen kann man im Prinzip schon. Alles, was man beim Bruchrechnen gelernt hat, muss man ja hier wiederum abrufen. Daher sind Bruchterme ein dankbares Stoffgebiet – wenn man schon top bei Brüchen war. Das Einzige, was wirklich bei Bruchtermen neu ist, ist die eingeschränkte Lösungsmenge sowie die auftretenden Variablen beim Bruch. Aber das Allerallerwichtigste ist: Alle Rechenoperationen sind bekannt! Das Addieren, das Subtrahieren, das Multiplizieren und das Dividieren sind schließlich zu 100 % gleich wie beim Bruchrechnen. Ebenso hat man bereits gelernt, wie man z. B. Variablen mittels des Distributivgesetzes auflöst – wenn man dieses bei Bruchtermen anwenden muss. Nichtsdestotrotz muss man natürlich beim Lösen jeder Aufgabe bei Bruchtermen hochkonzentriert sein – wie immer bei Mathe!

Weiterlesen „Mathematik-Nachhilfe: Aufgaben zu Bruchtermen, Teil 10“
Kategorien
Gleichungen Lineare Gleichungen Mathe Mathematik Nachhilfe Terme

Mathematik-Nachhilfe: Aufgaben zu linearen Gleichungen, Teil 5

Alle Gleichungen liefern ein “wahres“ Ergebnis © M. Großmann / PIXELIO

In Mathe ist die Bedeutung von Wörtern zentral, das führt man sich aber nicht immer bewusst vor Augen (wie das übrigens auch oft im realen Leben der Fall ist). Bei der Einführung von Gleichungen bzw. linearen Gleichungen (was ja die ersten im Fach Mathematik sind), bezieht sich die Bedeutung des Wortes auf die Terme rechts und links des Gleichheitszeichens („=“). Sind nämlich hierbei beide Terme gleich, also rechts und links des Gleichheitszeichens, dann ist die lineare Gleichung auch wahr (formal gesehen). 1 = 1 oder 25 = 25 ist ja beispielsweise nichts anderes als eine wahre Aussage. Sind die Terme jedoch nicht gleich, so liefert die Gleichung eine unwahre Aussage (formal gesehen), wie zum Beispiel: 1 ≠ 2 bzw. 25 ≠ 26.

Weiterlesen „Mathematik-Nachhilfe: Aufgaben zu linearen Gleichungen, Teil 5“
Kategorien
Gleichungen Mathe Mathematik Nachhilfe Rechenoperationen Satz des Pythagoras Terme

Mathematik-Nachhilfe: Aufgaben zum Satz des Pythagoras, Teil 4

Der Satz des Pythagoras © S. Hofschlaeger / PIXELIO

Bei einem rechtwinkligen Dreieck gilt der Satz des Pythagoras. Demzufolge gilt diese sehr berühmte Gesetzmäßigkeit nicht, wenn kein rechtwinkliges Dreieck vorliegt. Ist nun ein rechtwinkliges Dreieck gegeben, dann weist solch ein Dreieck immer eine Hypotenuse und zwei Katheten auf. Was ist aber was? Das ist ganz, ganz einfach – und sollte man deshalb auch nie vergessen. Die Hypotenuse ist immer die Seite im rechtwinkligen Dreieck, die sich gegenüber dem rechten Winkel befindet. Die anderen Seiten sind dann stets die Katheten, da die Hypotenuse ja immer festgelegt ist. Demzufolge ist auch stets klar, wenn man den Satz des Pythagoras an einem beliebigen rechtwinkligen Dreieck aufgestellt, was für eine Gleichung sich ergibt bzw. ergeben muss .

Weiterlesen „Mathematik-Nachhilfe: Aufgaben zum Satz des Pythagoras, Teil 4“
Kategorien
Funktionen Gleichungen Mathe Mathematik Nachhilfe Terme

Mathematik-Nachhilfe: Aufgaben zum Stoffgebiet Funktionen, Teil 4

Eine lineare Funktion als Graph dargestellt © Honina

Funktionen sind eindeutige Zuordnungen. Das ist ihr Charakteristikum. Ist das bei einer Funktion der Fall, dass eine eindeutige Zuordnung vorliegt, so kann man in Mathe hierzu einen Funktionsterm aufstellen. Dieser Funktionsterm gibt ganz allgemein die Zuordnung wieder. Man kann solch eine eindeutige Zuordnung jedoch nicht nur algebraisch durch einen Term bestimmen, sondern auch graphisch. Eine Funktion kann schließlich immer auch in ein Koordinatensystem eingezeichnet werden und ihr Verlauf sichtbar gemacht werden. Das nennt man den Graph einer Funktion. Daher kann man auch immer sowohl algebraisch als auch mittels eines Koordinatensystems eindeutig sagen, ob wirklich eine Funktion vorliegt – oder nicht. Es gibt in der Mathematik ja nicht nur Funktionen, das heißt, eindeutige Zuordnungen, sondern auch Relationen, uneindeutige Zuordnungen.

Weiterlesen „Mathematik-Nachhilfe: Aufgaben zum Stoffgebiet Funktionen, Teil 4“