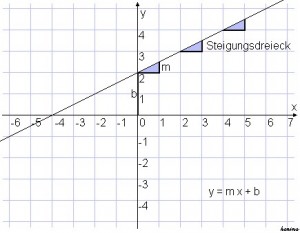
Eine Funktion kann man in Mathe immer grafisch darstellen, und zwar in einem Koordinatensystem. Diesen optischen Verlauf einer Funktion nennt man den Graph der Funktion. Einfache Funktionen wie lineare Funktionen und quadratische Funktionen kann man hierbei recht einfach in ein Koordinatensystem einzeichnen. Bei höheren Funktionen wie ganzrationale Funktionen 3. oder 4. Grades oder gebrochenrationalen Funktionen ist das schon um einiges schwieriger. Umso wichtiger ist es daher, dass bei solchen Funktionen vorher eine genaue Wertetabelle aufgestellt wird, die in einem bestimmten Intervall aufs Beste den Verlauf der Funktion optisch veranschaulicht. Was bei einer Funktion aber alles zu beachten ist, das lernt man in Mathematik schrittweise bzw. von Funktion zu Funktion – und das ab der Mittelstufe.