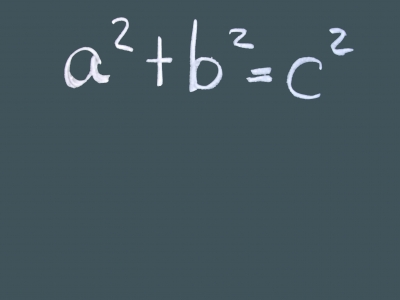Kategorie: Gleichungen

Kategorien
Gleichungen Mathe Mathematik Nachhilfe Ungleichungen

Mathematik-Nachhilfe: Aufgaben zu linearen Ungleichungen, Teil 7

Die Kardinalregel bei Ungleichungen!!! © Thommy Weiss / PIXELIO

Die wichtigste Regel in Mathe beim Lösen von Ungleichungen ist (das gilt für lineare Ungleichungen und ebenso für alle anderen Ungleichungen): Bei einer Multiplikation mit einer negativen Zahl oder einer Division mit einer negativen Zahl dreht sich bei der Ungleichung das Ungleichheitszeichen um. Das ist superwichtig, es ist schließlich die Kardinalregel bei Ungleichungen. Macht man also z. B. ein „mal (–5)“ / „· (–5)“ so ändert sich beispielsweise das < hin zu >. Macht man hingegen ein „durch (–4)“ / „: (–4)“ so ändert sich ebenso beispielsweise das > hin zu <. Das sollte man bei Ungleichungen so schnell wie möglich verinnerlichen. Wendet man die Kardinalregel bei Ungleichungen nämlich nicht an – so ist auch die spätere Lösungsmenge definitiv falsch. Wenn man aber geschickt umformt, dann kann man sich einen Wechsel des Ungleichheitszeichens ersparen!

Weiterlesen „Mathematik-Nachhilfe: Aufgaben zu linearen Ungleichungen, Teil 7“
Kategorien
Gleichungen Mathe Mathematik Nachhilfe Terme

Mathematik-Nachhilfe: Aufgaben zum Stoffgebiet Term, Teil 13

Ein Gespräch zwischen Termen © Uwe Wagschal / PIXELIO

„Was für ein Typ bist du denn?“, fragt ein Term einen anderen Term.

„Ich bin ein Produkt-Term. Und du?“

„Was denkst du denn?“, erwidert jener.

„Da muss ich dich erst einmal genau anschauen, damit ich das ganz genau sagen kann. „Einen Moment bitte“, antwortet dieser.

Ein paar Sekunden später.

„Du bist eine algebraische Summe.“

„Ja, das stimmt“, entgegnet schließlich der Term dem anderen Term.

Gäbe es Gespräche unter Termen, dann könnten viele hiervon tagtäglich so vonstattengehen. Das Ergebnis, mit welchem Term-Typ man es gerade verbal zu tun hat, würde hierbei natürlich je nach Typ unterschiedlich ausfallen – da ja normalerweise die letzte zu tätigende Rechenoperation den Typ des Terms bestimmt.

Weiterlesen „Mathematik-Nachhilfe: Aufgaben zum Stoffgebiet Term, Teil 13“
Kategorien
Funktionen Gleichungen Lineare Funktionen Mathe Mathematik Nachhilfe Terme

Mathematik-Nachhilfe: Aufgaben zu linearen Funktionen, Teil 2

Neuigkeiten aus dem Mathe-Unterricht © Tim Reckmann / PIXELIO

Als Schülerin und Schüler lernt man in Mathe als erste Funktionen lineare Funktionen kennen. „Das sind Geraden“, sagt ein emsiger Eleve, als er von seinen Eltern gefragt wird, was das ist. „Den Graphen einer linearen Funktion nennt man Gerade“, antwortet der Lehrer bei einem Elternabend auf die gleiche Frage einer Elternhälfte. Der Lehrer muss das auch haargenau so sagen, denn die Darstellung einer linearen Funktion in einem Koordinatensystem ergibt eine Gerade. „Lineare Funktionen kann man aber nicht nur im Koordinatensystem darstellen“, ergänzt er weiter. „Lineare Funktionen weisen auch einen Funktionsterm auf, anhand dessen man verschiedene Berechnungen machen kann – die auch wiederum an deren Graph ablesbar sind.“ „Aha“, hört man dann die Eltern sagen.

Weiterlesen „Mathematik-Nachhilfe: Aufgaben zu linearen Funktionen, Teil 2“
Kategorien
Bruchterme Gleichungen Mathe Mathematik Nachhilfe

Mathematik-Nachhilfe: Aufgaben zu Bruchtermen, Teil 10

Bruchterme sind super © Esther Stosch / PIXELIO

Alle Aufgaben in Mathe zu Bruchtermen kann man im Prinzip schon. Alles, was man beim Bruchrechnen gelernt hat, muss man ja hier wiederum abrufen. Daher sind Bruchterme ein dankbares Stoffgebiet – wenn man schon top bei Brüchen war. Das Einzige, was wirklich bei Bruchtermen neu ist, ist die eingeschränkte Lösungsmenge sowie die auftretenden Variablen beim Bruch. Aber das Allerallerwichtigste ist: Alle Rechenoperationen sind bekannt! Das Addieren, das Subtrahieren, das Multiplizieren und das Dividieren sind schließlich zu 100 % gleich wie beim Bruchrechnen. Ebenso hat man bereits gelernt, wie man z. B. Variablen mittels des Distributivgesetzes auflöst – wenn man dieses bei Bruchtermen anwenden muss. Nichtsdestotrotz muss man natürlich beim Lösen jeder Aufgabe bei Bruchtermen hochkonzentriert sein – wie immer bei Mathe!

Weiterlesen „Mathematik-Nachhilfe: Aufgaben zu Bruchtermen, Teil 10“
Kategorien
Gleichungen Lineare Gleichungen Mathe Mathematik Nachhilfe Terme

Mathematik-Nachhilfe: Aufgaben zu linearen Gleichungen, Teil 5

Alle Gleichungen liefern ein „wahres“ Ergebnis © M. Großmann / PIXELIO

In Mathe ist die Bedeutung von Wörtern zentral, das führt man sich aber nicht immer bewusst vor Augen (wie das übrigens auch oft im realen Leben der Fall ist). Bei der Einführung von Gleichungen bzw. linearen Gleichungen (was ja die ersten im Fach Mathematik sind) bezieht sich die Bedeutung des Wortes auf die Terme rechts und links des Gleichheitszeichens („=“). Sind nämlich hierbei beide Terme gleich, also rechts und links des Gleichheitszeichens, dann ist die lineare Gleichung auch wahr (formal gesehen). 1 = 1 oder 25 = 25 ist ja beispielsweise nichts anderes als eine wahre Aussage. Sind die Terme jedoch nicht gleich, so liefert die Gleichung eine unwahre Aussage (formal gesehen), wie zum Beispiel: 1 ≠ 2 bzw. 25 ≠ 26.

Weiterlesen „Mathematik-Nachhilfe: Aufgaben zu linearen Gleichungen, Teil 5“