
Es gibt bei einer quadratischen Gleichung verschiedene rechnerische Lösungsverfahren. Wendet man diese korrekt an, ergeben jene allesamt das richtige Ergebnis. So funktioniert ja Mathe! Wie gelingt das einem aber? Das Stichwort ist hier: Fleiß! Auch wenn man am Anfang vielleicht nicht zur Gänze verstanden hat, wie die p-q-Formel oder das quadratische Ergänzen funktioniert, dann sollte man auf keinen Fall „den Kopf in den Sand stecken“. Vielmehr sollte man eigenständig versuchen Aufgaben zu lösen. Die Aufgaben überprüft man dann im Unterricht oder mit den gemachten Aufgaben von KlassenkameradInnen. Irgendwann macht es dann nämlich „klick“. Das passiert aber nur, wenn man weiter intensiv die Aufgaben macht – und genau guckt, wie man mittels eines Lösungsverfahren zur Lösung einer quadratischen Gleichung kommt und was man für Fehler hierbei evtl. gemacht hat.
Aufgaben zum Mathe-Stoffgebiet quadratische Gleichung
1. Mathematik-Nachhilfe-Aufgabe: Ermittle graphisch die Lösungsmenge der quadratischen Gleichung.
a) 2a² + 2 = a
b) x² = 2x
c) y² – 1 – 1,5y = 0
d) x² = 0
2. Mathe-Nachhilfe-Aufgabe: Bestimme die Lösungsmenge der quadratischen Gleichung. Wende hierfür das quadratische Ergänzen an.
a) –$\frac{1}{3}$x2 – 5x + 18 = 0
b) 0,5a² + 4a + 10 = 0
c) 0,1x² + 1,5x – 3,4 = 0
d) y² + 20y + 36 = 0
3. Mathematik-Nachhilfe-Aufgabe: Ermittle die Lösung der quadratischen Gleichung. Ziehe hierfür die p-q-Formel heran.
a) x² + 40x + 39 = 0
b) 2z² + 15z + 28 = 0
c) 3a² – 1,6a – 0,75 = 0
d) 0 = –9y + y² + 18

Lösungen zum Mathematik-Stoffgebiet Quadratische Gleichungen
1. Mathe-Nachhilfe-Aufgabe: Bestimme mittels des graphischen Lösungsverfahrens die Lösung der quadratischen Gleichung.
a)
2a² + 2 = a | : 2
a2 + 1 = $\frac{1}{2}$a | – 1
a2 = $\frac{1}{2}$a – 1
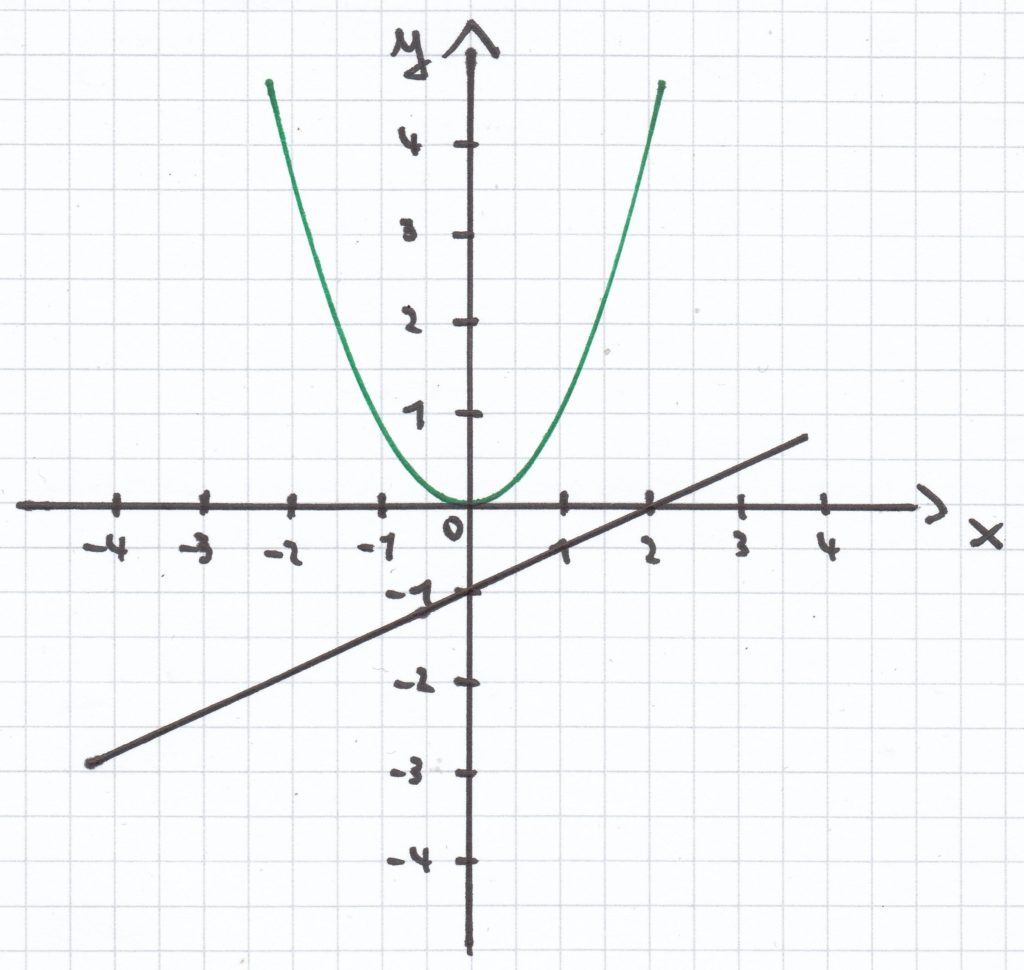
L = { } bzw. Ø
b)
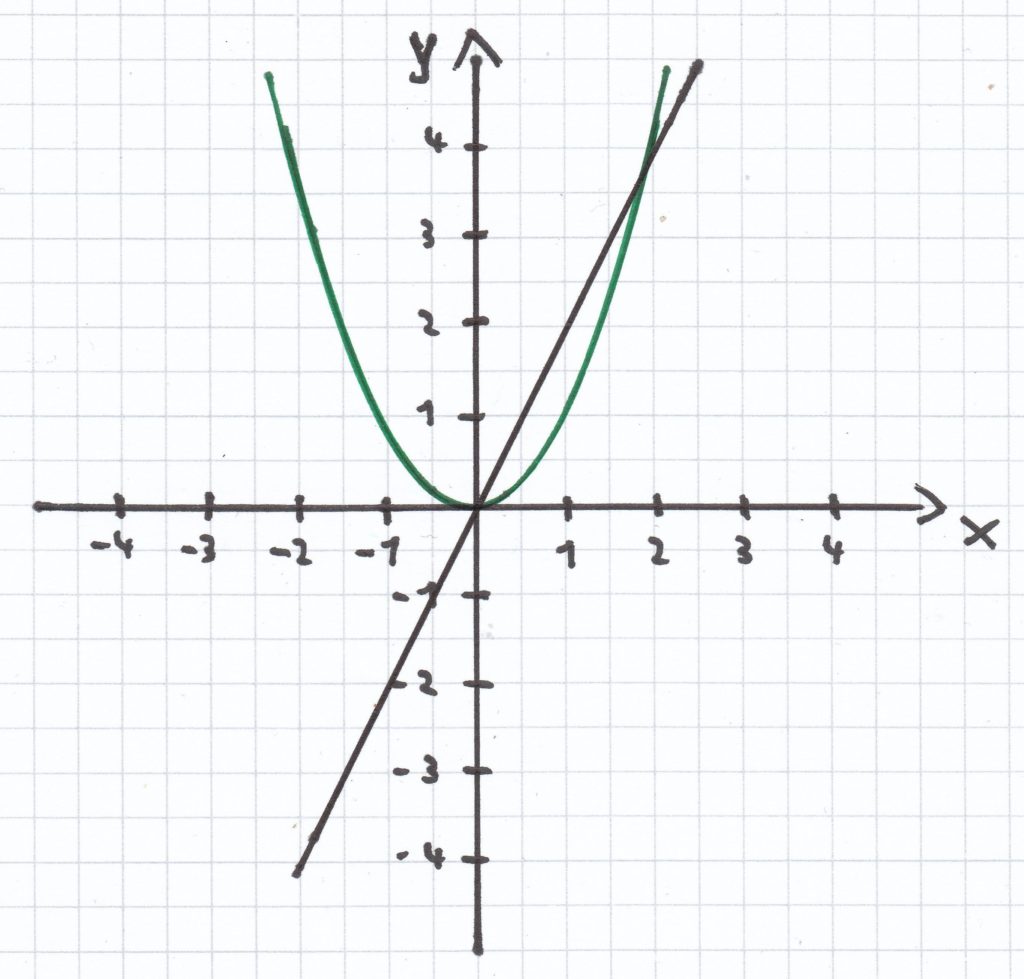
L = {0; 2}
c)
y² – 1 – 1,5y = 0 | + 1,5y
y² – 1 = 1,5y | + 1
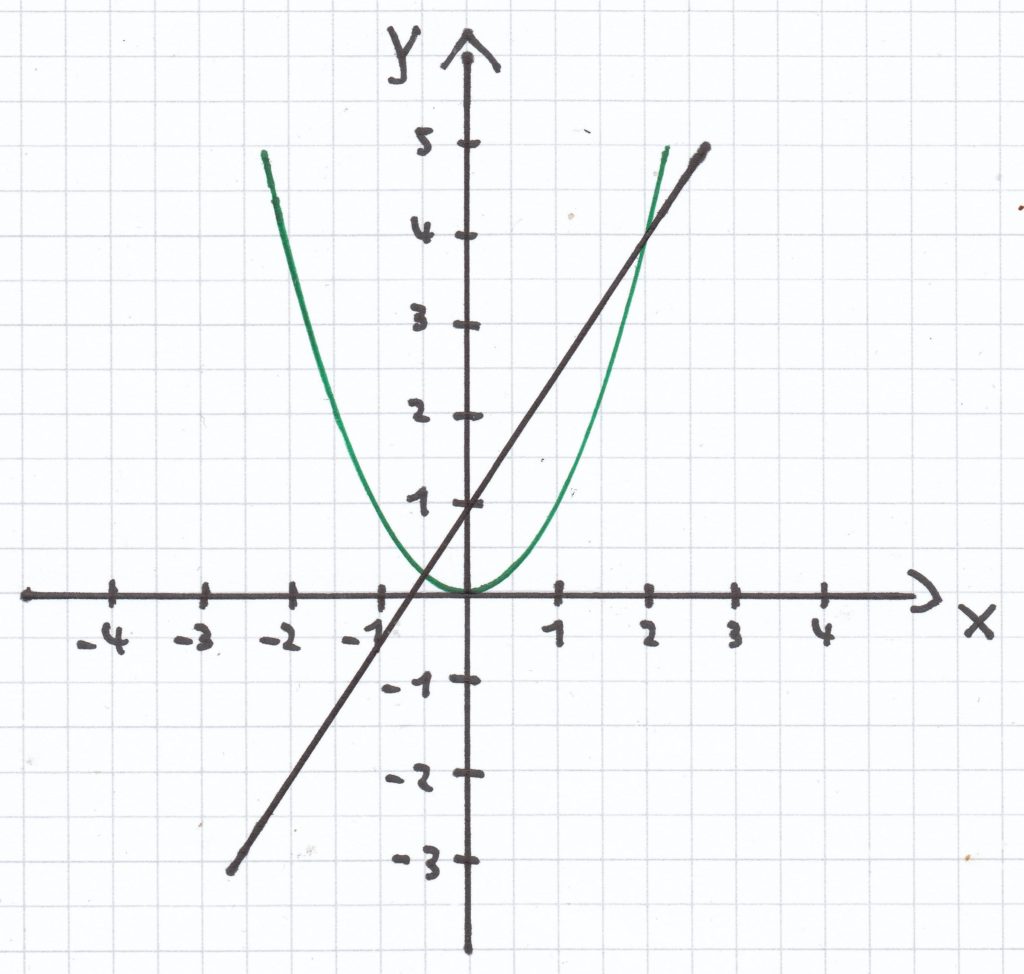
L = {–0,5; 2}
d)
x² = 0
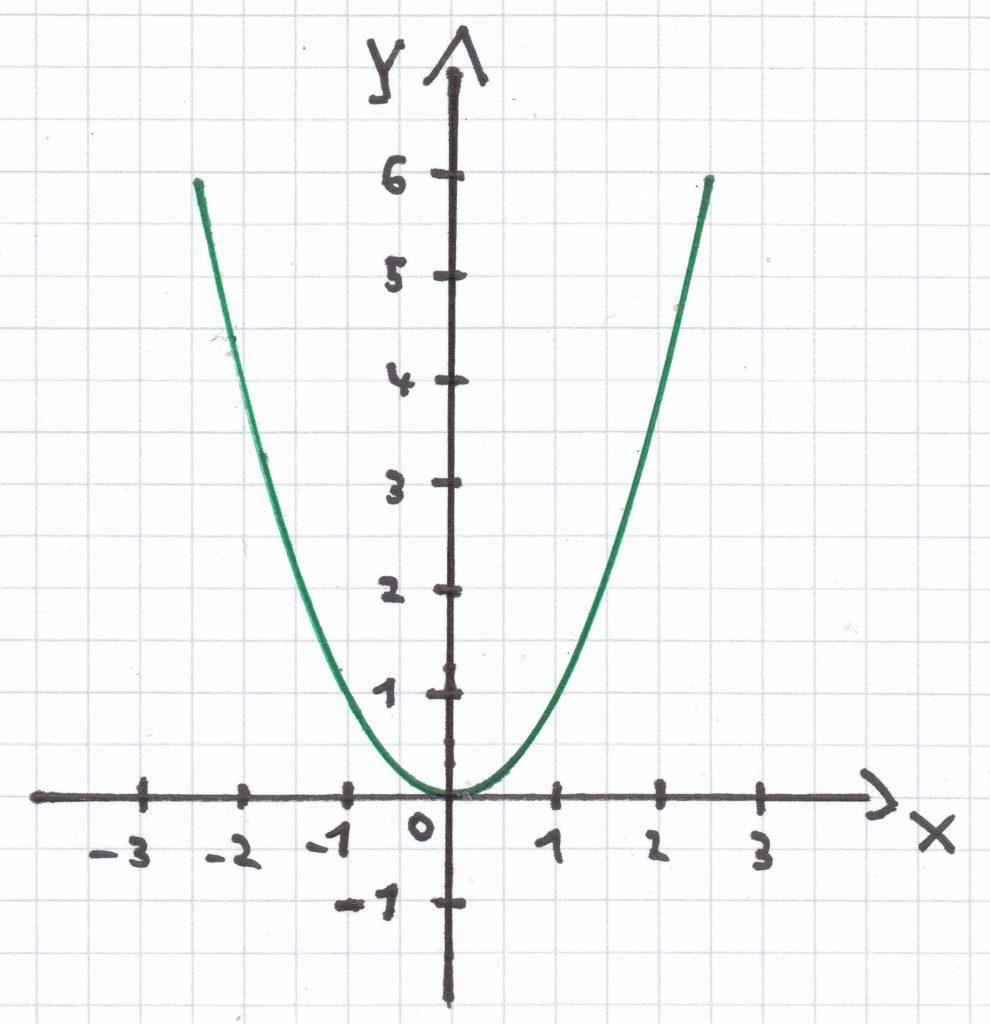
L = {0}
2. Mathematik-Nachhilfe-Aufgabe: Bestimme mittels quadratischer Ergänzung die Lösung der quadratischen Gleichungen.
a)
–$\frac{1}{3}$x2 – 5x + 18 = 0 | · (–3)
x² + 15x – 54 = 0
x² + 15x + ($\frac{15}{2}$)2 – 54 = ($\frac{15}{2}$)2
(x + 7,5)² – 54 = 56,25 | + 54
(x + 7,5)² = 110,25 | √
x + 7,5 = ± $\sqrt{110,25}$
x + 7,5 = ± 10,5 | – 7,5
x = ± 10,5 – 7,5
x1 = 10,5 – 7,5
x1 = 3
x2 = –10,5 – 7,5
x2 = –18
L = {–18; 3}
b)
0,5a² + 4a + 10 = 0 | · 2
a² + 8a + 20 = 0
a² + 8a + ($\frac{8}{2}$)2 + 20 = ($\frac{8}{2}$)2
(a + 4)2 + 20 = ($\frac{8}{2}$)2 | – 20
(a + 4)² = –4 | √
a + 4 = ± $\sqrt{-4}$
a + 4 = n. d.
L = { } bzw. Ø
c)
0,1x² + 1,5x – 3,4 = 0 | · 10
x² + 15x – 34 = 0
x² + 15x + ($\frac{15}{2}$)2 – 34 = ($\frac{15}{2}$)2 | + 34
(x + 7,5)² = 90,25 | √
x + 7,5 = ± 9,5 | – 7,5
x = ± 9,5 – 7,5
x1 = 9,5 – 7,5
x1 = 2
x2 = –9,5 – 7,5
x2 = –17
L = {–17; 2}
d)
y² + 20y + 36 = 0
y² + 20y + ($\frac{20}{2}$)2 + 36 = ($\frac{20}{2}$)2
(y + 10)² + 36 = 100 | – 36
(y + 10)² = 64 | √
y + 10 = ± 8 | – 10
y = ± 8 – 10
y1 = 8 – 10
y1 = –2
y2 = –8 – 10
y2 = –18
L = {–18; –2}
3. Mathe-Nachhilfe-Aufgabe: Bestimme mittels der p-q-Formel die Lösung der quadratischen Gleichung.
a)
x² + 40x + 39 = 0
x1,2 = –$\frac{40}{2}$ ± $\sqrt{(\frac{40}{2})^2~-~39)}$
x1,2 = –20 ± $\sqrt{400~-~39)}$
x1,2 = –20 ± $\sqrt{361}$
x1,2 = –20 ± 19
x1 = –20 + 19
x1 = –1
x2 = –20 – 19
x2 = –39
L = {–39; –1}
b)
2z² + 15z + 28 = 0 | : 2
z² + 7,5z + 14 = 0
z1,2 = –$\frac{7,5}{2}$ ± $\sqrt{(\frac{7,5}{2})^2~-~14)}$
z1,2 = –3,75 ± $\sqrt{14,0625~-~14)}$
z1,2 = –3,75 ± $\sqrt{0,0625}$
z1,2 = –3,75 ± 0,25
z1 = –3,75 + 0,25
z1 = –3,5
z2 = –3,75 – 0,25
z2 = –4
L = {–4; –3,5}
c)
3a² – 1,6a – 0,75 = 0 | : 3
a2 – $\frac{8}{15}$ – 0,25 = 0
a1,2 = \frac{8}{\frac{15}{2}} ± $\sqrt{(\frac{8}{\frac{15}{2}})^2~+~0,25)}$
a1,2 = $\frac{4}{15}$ ± $\sqrt{\frac{16}{225}~+~0,25)}$
a1,2 = $\frac{4}{15}$ ± $\sqrt{\frac{289}{900}}$
a1,2 = $\frac{4}{15}$ ± $\frac{17}{30}$
a1 = $\frac{4}{15}$ – $\frac{17}{30}$ = –$\frac{3}{10}$
a2 = $\frac{4}{15}$ + $\frac{17}{30}$ = $\frac{5}{6}$
L = {–$\frac{3}{10}$; $\frac{5}{6}$}
d)
0 = –9y + y² + 18
y² – 9y + 18 = 0
y1,2 = $\frac{9}{2}$ ± $\sqrt{(\frac{9}{2})^2~-~18)}$
y1,2 = 4,5 ± $\sqrt{\frac{81}{4}~-~18)}$
y1,2 = 4,5 ± $\sqrt{2,25}$
y1,2 = 4,5 ± 1,5
y1 = 4,5 + 1,5
y1 = 6
y2 = 4,5 – 1,5
y2 = 3
L = {3; 6}