1. Funktionsterme einer ganzrationalen Funktion
Der Funktionsterm einer linearen Funktion, a0 + a1x, lässt sich durch die Addition eines Vielfachen von x2 zu diesem Term hin verändern:
a0 + a1x + a2x2.
Hierdurch erhält man eine quadratische Funktion. Macht man nun mit höheren Potenzen von x auf die gleiche Weise weiter, so erhält man Terme, die folgende Form vorweisen:
anxn + an– 1xn – 1 + … + a1x + a0.
Solch ein Gebilde wird als Polynom bezeichnet. Hieraus kann man unendlich viele neue Funktionen bilden.
Definition einer ganzrationalen Funktion:
Eine Funktion, bei der jedes n Є ℕ ist, und die folgende Zuordnungsvorschrift hat:
f: ↦ anxn + an – 1xn – 1 + … + a1x + a0
(Zuordnungsvorschrift ganzrationale Funktion),
heißt ganzrationale Funktion.
Die Koeffizienten an, an– 1, …, a0 sind hierbei reelle Zahlen. Bei an ≠ 0 hat f den Grad n bzw. handelt es sich dann um eine ganzrationale Funktion n-ten Grades.
Beispiele:
f(x) = a1x + a0 besitzt den Grad 1 bzw. es handelt sich hier um eine ganzrationale Funktion 1. Grades.
f(x) = a2x2 + a1x + a0 besitzt den Grad 2 bzw. es handelt es sich hier um eine ganzrationale Funktion 2. Grades.
f(x) = a3x3 + a2x2 + a1x + a0 besitzt den Grad 3 bzw. es handelt sich hier um eine ganzrationale Funktion 3. Grades.
f(x) = anxn + an – 1xn – 1 + … + a1x + a0 besitzt den Grad n bzw. es handelt sich hier um eine ganzrationale Funktion n-ten Grades.
2. Verschiedene ganzrationale Funktionen
Nachfolgend werden verschiedene ganzrationale Funktionen, beginnend von dem 1. Grad bis zum 4. Grad, aufgezeigt und auch deren Graphen visualisiert.
2.1 Lineare Funktionen: ganzrationale Funktionen 1. Grades
Der Funktionsterm einer ganzrationalen Funktion 1. Grades ist folgender:
f(x) = a1x + a0
Es handelt sich hierbei um eine lineare Funktion.
Das Schaubild einer solchen Funktion stellt eine Gerade dar.
Beispiele:
1.
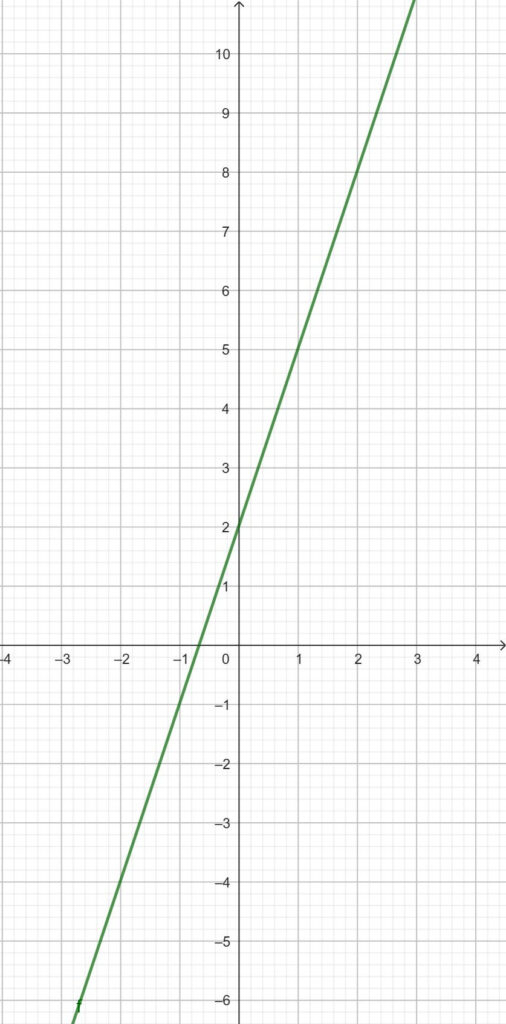
Es ist diese Zuordnungsvorschrift gegeben:
x ↦ 3x + 2
(Zuordnungsvorschrift einer linearen Funktion mit positiver Steigung)
Die Funktionsgleichung ist hierbei folgende:
f(x) = 3x + 2
Der Graph der Funktion ist dieser:
2.
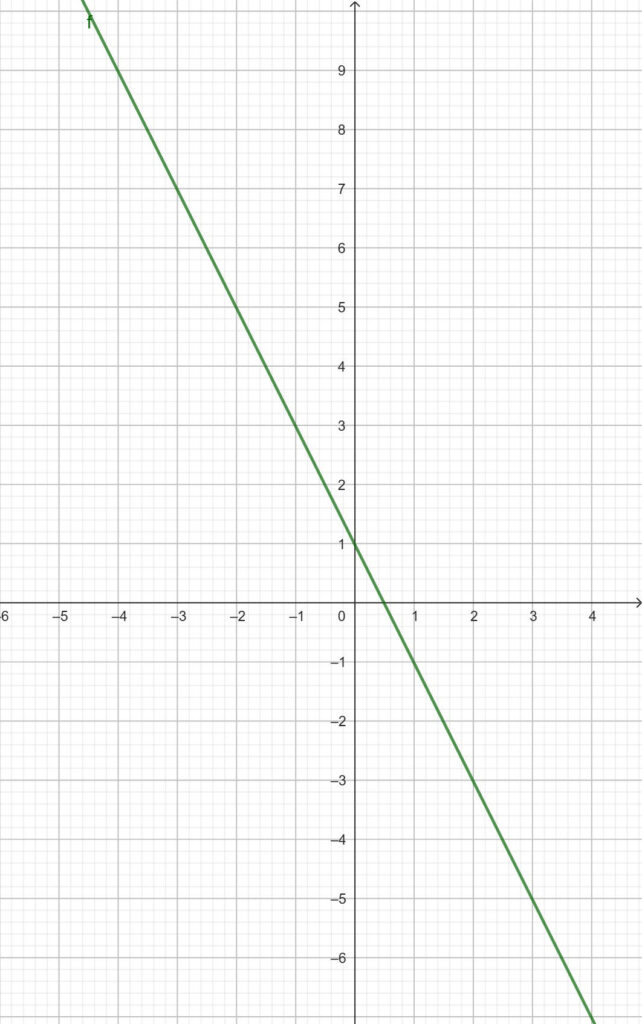
Es ist diese Zuordnungsvorschrift gegeben:
x ↦ –2x + 1
(Zuordnungsvorschrift einer linearen Funktion mit negativer Steigung)
Die Funktionsgleichung ist hierbei folgende:
f(x) = –2x + 1
Der Graph der Funktion ist dieser:
2.2 Quadratische Funktionen: ganzrationale Funktionen 2. Grades
Der Funktionsterm einer ganzrationalen Funktion 2. Grades ist dieser:
f(x) = a2x2 + a1x + a0
Es handelt sich hierbei um eine quadratische Funktion.
Der Graph einer solchen Funktion stellt eine Parabel dar.
Beispiele:
1.
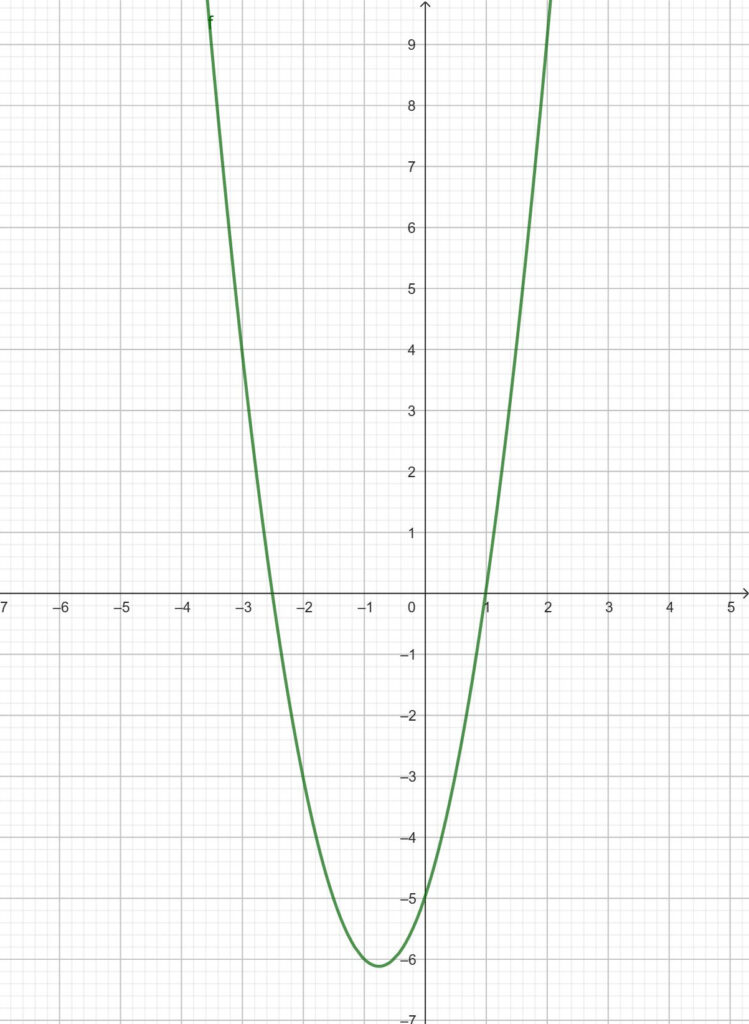
Es ist diese Zuordnungsvorschrift gegeben:
x ↦ 2x2 + 3x – 5
(Zuordnungsvorschrift einer quadratischen Funktion mit nach oben geöffneter Parabel)
Die Funktionsgleichung ist hierbei folgende:
f(x) = 2x2 + 3x – 5
Der Graph der Funktion ist dieser:
2.
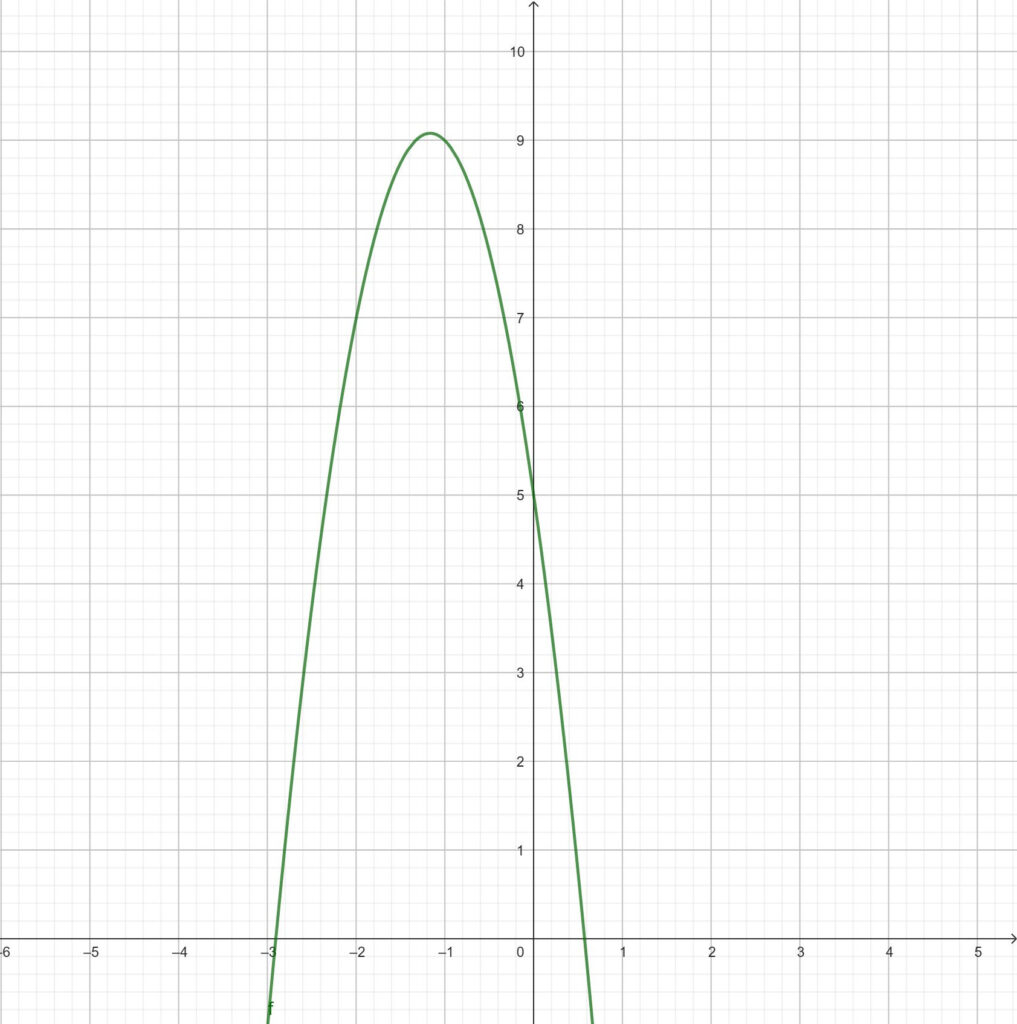
Es ist folgende Zuordnungsvorschrift gegeben:
x ↦ –3x2 – 7x + 5
(Zuordnungsvorschrift einer quadratischen Funktion mit nach unten geöffneter Parabel)
Die Funktionsgleichung ist hierbei diese:
f(x) = –3x2 – 7x + 5
Der Graph der Funktion ist folgender:
2.3 Kubische Funktionen: ganzrationale Funktionen 3. Grades
Der Funktionsterm einer ganzrationalen Funktion 3. Grades ist folgender:
f(x) = a3x3 + a2x2 + a1x + a0
Es handelt sich hierbei um eine kubische Funktion.
Der Graph einer solchen Funktion stellt eine kubische Kurve dar.
Beispiele:
1.
Es ist folgende Zuordnungsvorschrift gegeben:
x ↦ 2x3 + 7x2 – 4x – 9
(Zuordnungsvorschrift einer kubischen Funktion)
Die Funktionsgleichung ist hierbei folgende:
f(x) = 2x3 + 7x2 – 4x – 9
Der Graph der Funktion ist dieser:

2.
Es ist folgende Zuordnungsvorschrift gegeben:
x ↦ –3x3 – 5x2 + 12x – 4
(Zuordnungsvorschrift einer kubischen Funktion)
Die Funktionsgleichung ist hierbei diese:
f(x) = –3x3 – 5x2 + 12x – 4
Der Graph der Funktion ist folgender:
2.4 Ganzrationale Funktionen 4. Grades
Der Funktionsterm einer ganzrationalen Funktion 4. Grades ist dieser:
f(x) = a4x4 + a3x3 + a2x2 + a1x + a0
Es handelt sich hierbei um eine ganzrationale Funktion 4. Grades.
Beispiele:
1.
Es ist folgende Zuordnungsvorschrift gegeben:
x ↦ 3x4 – 8x3 + 4x2 – 2x + 5
(Zuordnungsvorschrift einer ganzrationalen Funktion 4. Grades)
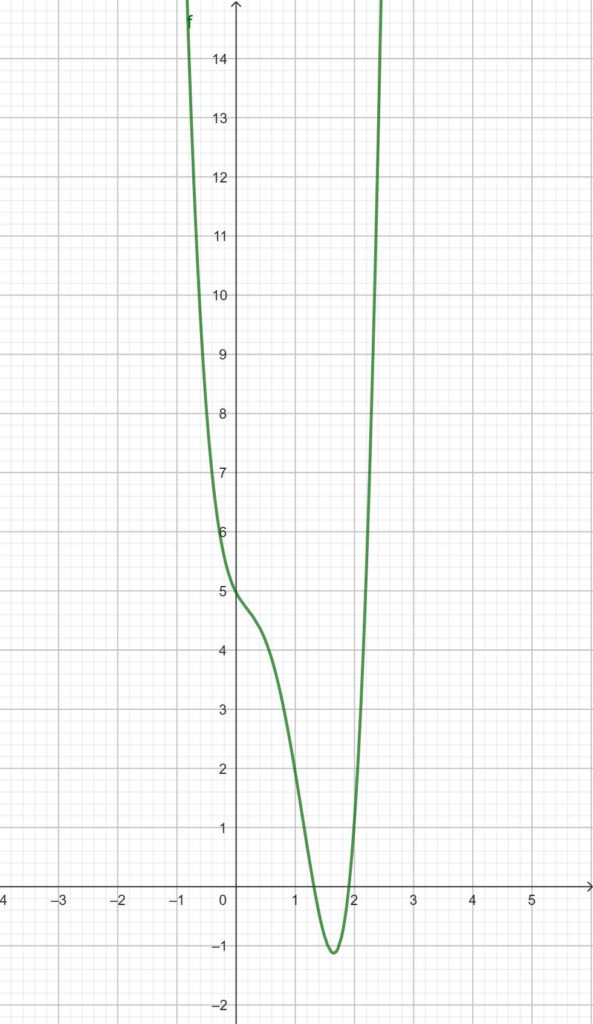
Die Funktionsgleichung ist hierbei diese:
f(x) = 3x4 – 8x3 + 4x2 – 2x + 5
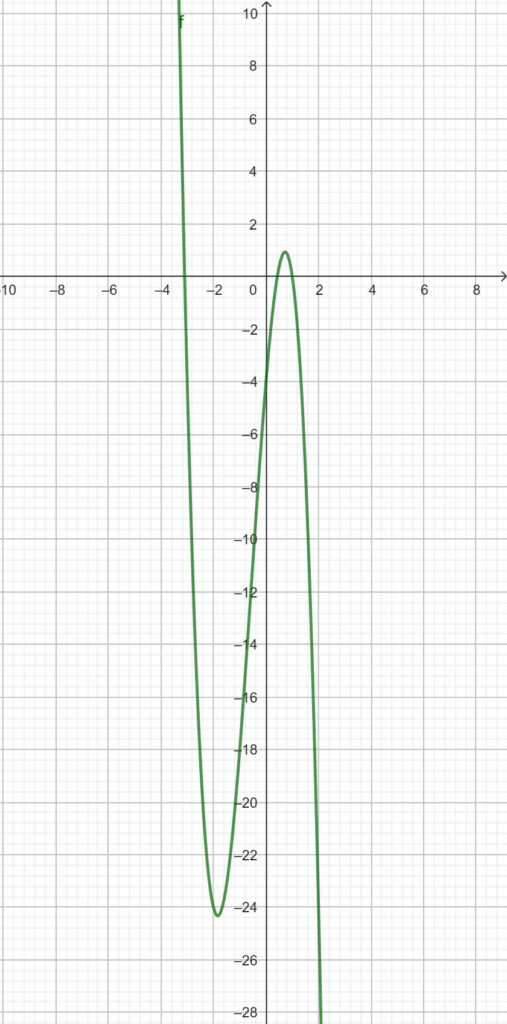
Der Graph der Funktion ist folgender:
2.
Es ist diese Zuordnungsvorschrift gegeben:
x ↦ –2x4 + 2x3 + 4x2 + 3x – 9
(Zuordnungsvorschrift einer ganzrationalen Funktion 4. Grades)
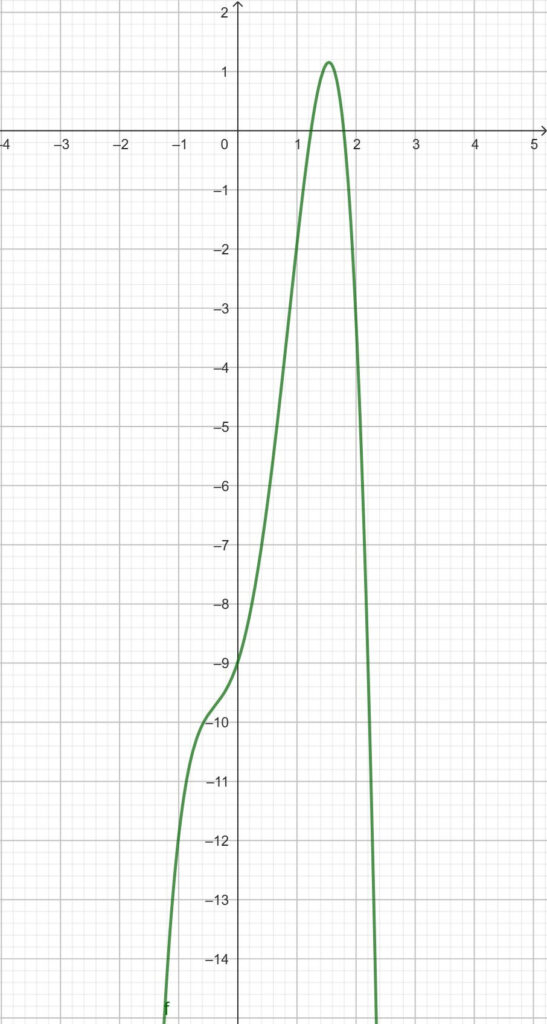
Die Funktionsgleichung ist hierbei diese:
f(x) = –2x4 + 2x3 + 4x2 + 3x – 9
Der Graph der Funktion ist folgender:
2.5 Granzrationale Funktionen höheren Grades
Bei weiteren ganzrationalen Funktionen höheren Grades ist wie bei allen ganzrationalen Funktionen für das Verhalten der Funktion ins Unendliche der höchste Exponent des bestimmenden Polynoms, des namensgebenden (1. Grades, 2. Grades usw., also das Erste), maßgeblich.
Vom Koeffizienten des bestimmenden Polynoms hängt ab, wie die ganzrationale Funktion verläuft. Hierbei ergeben sich folgende Möglichkeiten:
Ist der Koeffizient ungerade und positiv, dann verläuft der Graph „von links unten nach rechts oben“.
Ist der Koeffizient ungerade und negativ, dann verläuft der Graph „von links oben nach rechts unten“.
Wenn der Koeffizient gerade und positiv ist, dann verläuft der Graph „links und rechts nach oben“.
Wenn der Koeffizient gerade und negativ ist, dann verläuft der Graph „links und rechts nach unten“.