Unter der Menge der natürlichen Zahlen gibt es eine Zahlenmenge, die seitdem Menschen sich mit Zahlen und der Mathematik beschäftigt haben, auf diese eine immense Faszination ausgeübt hat: die Primzahlen. Nachweislich haben sich bereits in der Antike die Griechen mit Primzahlen systematisch auseinandergesetzt und herausgefunden, dass es hiervon sehr viele gibt, und Verfahren genutzt (wie z. B. den „Sieb des Eratosthenes“), um Primzahlen bestimmen zu können. Warum werden aber diese Zahlen – bis heute – als außergewöhnlich angesehen? Zum einen sind Primzahlen einfach zu verstehen, zum anderen schwierig zu durchdringen. Sie beinhalten viel an Verschiedenem, das einfach und für viele zugänglich ist, aber auch entschieden Komplexeres, das nur für wenige erfassbar ist. Das ist der Grund.
Definition und Bestimmen von Primzahlen
Was Primzahlen sind. Das ist simpel. Dafür gibt es eine einfache Definition: Bei einer Primzahl handelt es sich um eine Zahl, die nur durch sich selbst und 1 teilbar ist. Eine Primzahl weist also IMMER zwei Teiler auf. Aufgrund dieser Definition ist die erste Primzahl die 2, da sie durch 2 und durch 1 teilbar ist (und nicht die 1, da die 1 nur einen Teiler aufweist). Aber gerade aufgrund jener Definition kann man ziemlich leicht zumindest die weiteren Primzahlen bis 20 bestimmen. Da alle geraden Zahlen (außer die 2) mindestens drei Teiler vorweisen (bspw. 4 Teiler: 1, 2, 4; 6 Teiler: 1, 2, 3, 6) kann eine gerade Zahl (außer die 2) niemals eine Primzahl sein. Bei den Zahlen bis 20 bleiben dann die Zahlen 3, 5, 7, 9, 11, 13, 15, 17 und 19 zunächst übrig. Hierbei fällt aber noch die 9 weg (da auch durch 3 teilbar) und die 15 (da auch durch 3 und ebenso durch 5 teilbar). Daher sind die Primzahlen von 1 bis 20 folgende: 2, 3, 5, 7, 11, 13, 17, 19. Diese zu bestimmen ist also leicht.
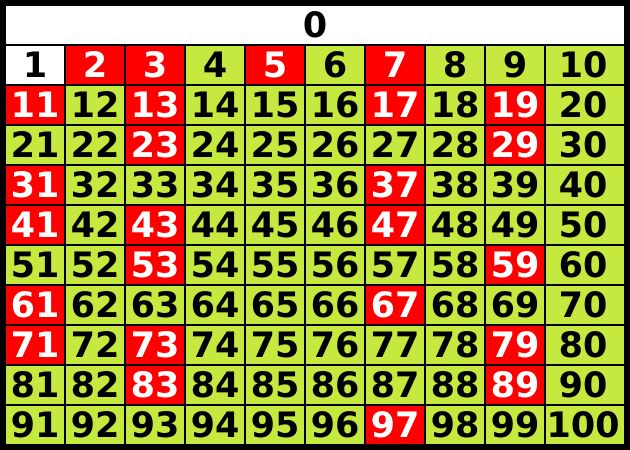
Bei den Primzahlen bis 100 verfährt man auf eine gewisse Weise genauso wie bei den Zahlen bis 20. Dazu gibt es das bekannte „Sieb des Eratosthenes“. Das Ermitteln der Primzahlen ist hierbei aber schon um einiges aufwändiger, sprich schwieriger, da man noch die Teiler 3, 5 und 7 heranziehen muss, um alle Nicht-Primzahlen auszuschließen.
Je größer die Zahl, desto schwieriger die Bestimmbarkeit einer Primzahl
Es leuchtet daher ein, dass je größer die Zahl ist, umso schwieriger wird es zu ermitteln, ob eine Primzahl vorliegt oder nicht. Sehr interessant ist hierbei folgende mathematische Feststellung: Je größer die Zahlen werden, desto weniger Primzahlen treten auf bzw. die sogenannte Primzahldichte nimmt ab. Hinzu kommt, dass es bis heute keine Formel gibt, mit der man ohne Weiteres eine Primzahl – egal wie groß – bestimmen kann. Denn Primzahlen sind im Prinzip „chaotisch“ auftretend, das heißt, es gibt kein vollständig erklärbares Muster.
Entdeckt man eine weitere Primzahl, die man durch aufwändige Testverfahren definitiv als Primzahl verifiziert, bekommt man daher nicht nur eine Belohnung mittels eines ziemlich hohen Preisgeldes (um die 100.000 US-Dollar), sondern auch einen Eintrag ins Guinness-Buch der Weltrekorde. Hierin befindet sich die Person, die die derzeit größte bekannte Primzahl – 2136279841 – ermitteln konnte. Diese riesenriesenriesengroße Primzahl enthält sage und schreibe – 41.024.320 Dezimalstellen! Das ist irre!
Jede Zahl in Primfaktoren zerlegbar
Sehr außergewöhnlich ist ebenso, dass jedwede Zahl in sogenannte Primfaktoren zerlegt werden kann. Hierdurch ist es möglich, zwischen verschiedenen Zahlen deren größten gemeinsamen Teiler (ggT) oder deren kleinstes gemeinsames Vielfaches zu ermitteln.
Die Zahlen 42 und 102 kann man in folgende Primfaktoren zerlegen:
42 = 2 · 3 · 7 und 102 = 2 · 3 · 17
Beim größten gemeinsamen Teiler (ggT) muss man nun überprüfen, welche Faktoren bei beiden Primfaktorzerlegungen vorkommen.
42 = 2 · 3 · 7 und 102 = 2 · 3 · 17, bei beiden sind die gleichen Faktoren: 2 · 3. Demzufolge ist der größte gemeinsame Teiler (ggT): 2 · 3 = 6.
Beim kleinsten gemeinsamen Vielfachen (kgV) muss man nun überprüfen, wo bei beiden Primfaktorzerlegungen jeweils die größten Potenzen vorkommen.
42 = 2 · 3 · 7 = 21 · 31 · 71 und 102 = 2 · 3 · 17 = 21 · 31 · 171
Wie man sieht, ist nach den Primfaktorzerlegungen beider Zahlen die größte Potenz 1, wobei die Primfaktoren 2 · 3 doppelt vorkommen. Daher ist das kleinste gemeinsame Vielfache (kgV):
21 · 31 · 71 171 = 714
Den größten gemeinsamen Teiler (ggT) und das kleinste gemeinsame Vielfache (kgV) kann man nun auch bei drei, vier, fünf oder beliebig vielen Zahlen mittels einer Primfaktorzerlegung bestimmen. In der Mathematik wird das auch als die „DNA“ der Zahlen bezeichnet, da sich jede Zahl größer 1 als Primzahl oder Produkt aus Primzahlen darstellen lässt.
Primzahlen stellen bedeutende Zahlen der mathematischen Forschung dar
Zwei berühmte ungelöste Vermutungen der Mathematik, die Mathematiker bis heute beschäftigen, beinhalten Primzahlen: die Goldbachsche und die Riemannsche Vermutung.
Die Goldbachsche Vermutung geht hierbei davon aus, dass jede gerade Zahl größer zwei als die Summe zweier Primzahlen wiedergegeben werden kann.
Beispiel: 4 = 2 + 2, 6 = 3 + 3, 8 = 5 + 3, 10 = 5 + 5, 12 = 7 + 5, 14 = 7 + 7, 16 = 11 + 5 usw.
Die Goldbachsche Vermutung, die am 07.06.1742 in einem Brief von Christian Goldbach an Leonhard Euler formuliert wurde, konnte bis heute nicht mathematisch bewiesen werden.
Die Riemannsche Vermutung aus dem Jahr 1859, die bis heute sogar das bedeutendste ungelöste Problem der reinen Mathematik darstellt, sagt einfach gesprochen aus, dass sich die Folge der Primzahlen 2, 3, 5, 7, 11, 13, 17, 19 usw. „möglichst zufällig“ verhält. Das zeigt sich beispielsweise dadurch, wenn man die Abfolge der Ereignisse betrachtet, dass eine natürliche Zahl eine gerade Zahl an Primfaktoren aufweist oder eine ungerade Zahl.
Die Zahl 4 = 2 · 2 hat zwei Primfaktoren (gerade), die Zahl 6 = 2 · 3 zwei Primfaktoren (gerade), die Zahl 8 = 2 · 2 · 2 drei Primfaktoren (ungerade), die Zahl 10 = 5 · 5 zwei Primfaktoren (gerade), die Zahl 12 = 2 · 3 · 3 drei Primfaktoren (ungerade), die Zahl 14 = 2 · 7 zwei Primfaktoren (gerade), die Zahl 16 = 2 · 2 · 2 · 2 vier Primfaktoren (gerade), die Zahl 18 = 2 · 3 · 3 drei Primfaktoren (ungerade), die Zahl 20 = 2 · 2 · 5 drei Primfaktoren (ungerade) usw.
Auf lange Sicht ist nach Riemann das Auftreten von gerade bzw. ungerade bei den Primfaktoren gerader Zahlen ein Verhalten, das sich „ähnlich zufällig“ verhält, wie ein Münzwurf mit „Kopf“ und „Zahl“, der unendlich oft durchgeführt wird.
Primzahlen als Basis der Kryptografie
Heutzutage kommen Primzahlen auch jederzeit bei vielen Verschlüsselungstechniken zum Einsatz, sodass Daten im Internet geschützt bleiben. Das nennt man Kryptografie und dient der Informationssicherheit. Aber warum werden hierfür gerade Primzahlen herangezogen? Bei Verschlüsselungsverfahren werden zwei sehr große Primzahlen (p und q) miteinander multipliziert (n = p · q). Die Multiplikation zweier großer Primzahlen ist sehr einfach, die Umkehrung, die Faktorisierung von n in seine Primfaktoren, aber äußerst schwierig, wenn die Zahlen sehr groß sind. Je größer die Primzahlen (p, q), die zur Verschlüsselung herangezogen werden, desto größer ist das Produkt (n = p · q) und desto schwieriger ist die Entschlüsselung des Verschlüsselungssystems bzw. – umso sicherer!
Wie man sieht, sind Primzahlen vor allem eines – ganz besondere Zahlen!