Höhensatz des Euklid

1. Allgemeines zum Höhensatz des Euklid

Neben dem Satz des Pythagoras und dem Kathetensatz des Euklid gibt es bei einem rechtwinkligen Dreieck noch eine andere auftretenden Gesetzmäßigkeit: den Höhensatz des Euklid. Es liegt hier eine Beziehung zwischen der dem rechten Winkel gegenüberliegende Seite des Dreiecks vor und dessen Höhe. Bei der vorliegenden Beziehung handelt es sich um eine sogenannte Flächengleichung, wie es auch bei dem Satz des Pythagoras und dem Höhensatz des Euklid der Fall ist.

2. Der Höhensatz des Euklid

Bei einem rechtwinkligen Dreieck teilt die Höhe h, ausgehend von der Hypothenuse, die gegenüberliegende Seite in zwei Abschnitte, die Abschnitte p und q. Hierbei entspricht die Fläche des Höhenquadrats der Fläche der Hypotenusenabschnitte p und q, die einem Rechteck entspricht.

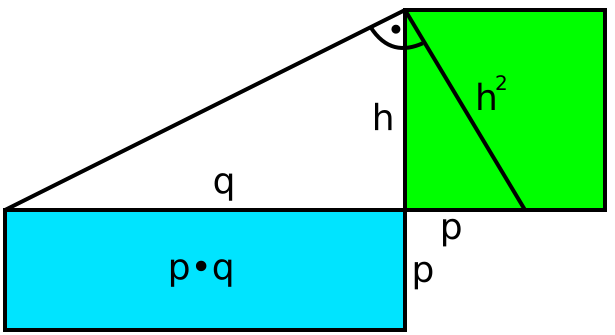
Dadurch ergibt sich diese Gleichung:

h² = p · q

Beispiele:

1. Es liegt ein rechtwinkliges Dreieck vor. Die Hypotenusenabschnitte sind: p = 4 cm, q = 9 cm. Gesucht ist die Höhe h des Dreiecks.

h² = p · q              | √

h = $\sqrt{\mathrm{p} ~\cdot~ \mathrm{q}}$

h = $\sqrt{\mathrm{4~cm} ~\cdot~ \mathrm{9~cm}}$

h = $\sqrt{\mathrm{36~cm}^2}$

h = 6 cm

2. Es ist eine rechtwinkliges Dreieck gegeben. Die Höhe ist h = 5 cm. Der Hypotenusenabschnitt p = 4 cm. Gesucht ist der Hypotenusenabschnitt q.

h² = p · q              | : p

$\frac{\mathrm{h}^2}{\mathrm{p}}$ = q

q = $\frac{\mathrm{h}^2}{\mathrm{p}}$

q = $\frac{\mathrm{5~cm}^2}{\mathrm{4~cm}}$

q = $\frac{\mathrm{25~cm}}{\mathrm{4~cm}}$

q = 6,25 cm

3. Es ist ein rechtwinkliges Dreieck gegeben. Die Höhe beträgt h = 6 cm. Die Hypotenuse ist 13 cm. Gesucht sind die Hypotenusenabschnitte p und q.

h² = p · q

l_h = p + q

Man löst nun die zweite Gleichung nach p oder q auf und setzt diese in die erste Gleichung ein.

l_h – q = p

p = l_h – q

h² = (lq – q) · q

h² = lq · q – q · q

h² = lq · q – q²              | – h²

0 = –q² + lq · q – h²              | · (–1)

0 = q² – lq · q + h²

q² – lq · q + h² = 0

q² – 13q + (6)² = 0

q² – 13q + 36 = 0

Man erhält nun eine quadratische Gleichung. Diese kann man mit der p-q-Formel auflösen.

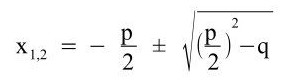
q_1,2 = $\frac{13}{2}$ cm ± $\sqrt{\left(\frac{13}{2}~\mathrm{cm}\right)^2 ~-~ 36~\mathrm{cm}^2}$

q_1,2 = 6,5 cm ± $\sqrt{\frac{169}{4} ~\mathrm{cm}^2~-~ 36~ \mathrm{cm}^2}$

q_1,2 = 6,5 cm ± $\sqrt{\mathrm{6,25~cm}^2}$

q_1,2 = 6,5 cm ± 2,5 cm

q₁ = 6,5 cm – 2,5 cm = 4 cm

q₂ = 6,5 cm + 2,5 cm = 9 cm

q ist entweder 4 cm oder 9 cm

Es gilt ja:

p = l_h – q

Daher ergibt sich:

p = 13 cm – 4 cm = 9 cm, bei q = 4 cm

oder:

p = 13 cm – 9 cm = 4 cm, bei q = 9 cm

Lösungen: p = 9 cm, q = 4 cm; p = 4 cm, q = 9 cm

3. Die Umkehrung des Höhensatzes des Euklid

Mittels des Höhensatz ist auch überprüfbar, ob ein Dreieck rechtwinklig ist oder nicht. Liegt in einem Dreieck mit der Höhe h und den Abschnitten p und q die Beziehung vor, dass h² = p · q gilt, dann ist das Dreieck rechtwinklig. Wird die Gleichung nicht erfüllt, dann ist das vorliegende Dreieck nicht rechtwinklig.

Beispiele:

1.

Es ist eine Dreieck mit der Höhe h = 3 cm und die Abschnitte, von der Höhe zur Grundseite getrennt, p = 2 cm und q = 4,5 cm gegeben. Es soll überprüft werden, ob das Dreieck rechtwinklig ist.

Wenn das Dreieck rechtwinklig ist, dann muss diese Gleichung eine wahre Aussage liefern:

h² = p · q

(3)² = 2 cm · 4,5 cm

9 cm² = 9 cm²

Die Gleichung ergibt eine wahre Aussage. Demzufolge ist das Dreieck rechtwinklig.

2.

Ein Dreieck hat die Höhe h = 4 cm und die von der Höhe zur Grundseites getrennten Abschnitte p = 2 und q = 6 cm.

Ist das Dreieck rechtwinklig, dann ist diese Gleichung wahr:

h² = p · q

(4)2 = 2 cm · 6 cm

16 cm² = 12 cm²

Die Gleichung liefert keine wahre Aussage. Daher handelt es sich hier um kein rechtwinkliges Dreieck.