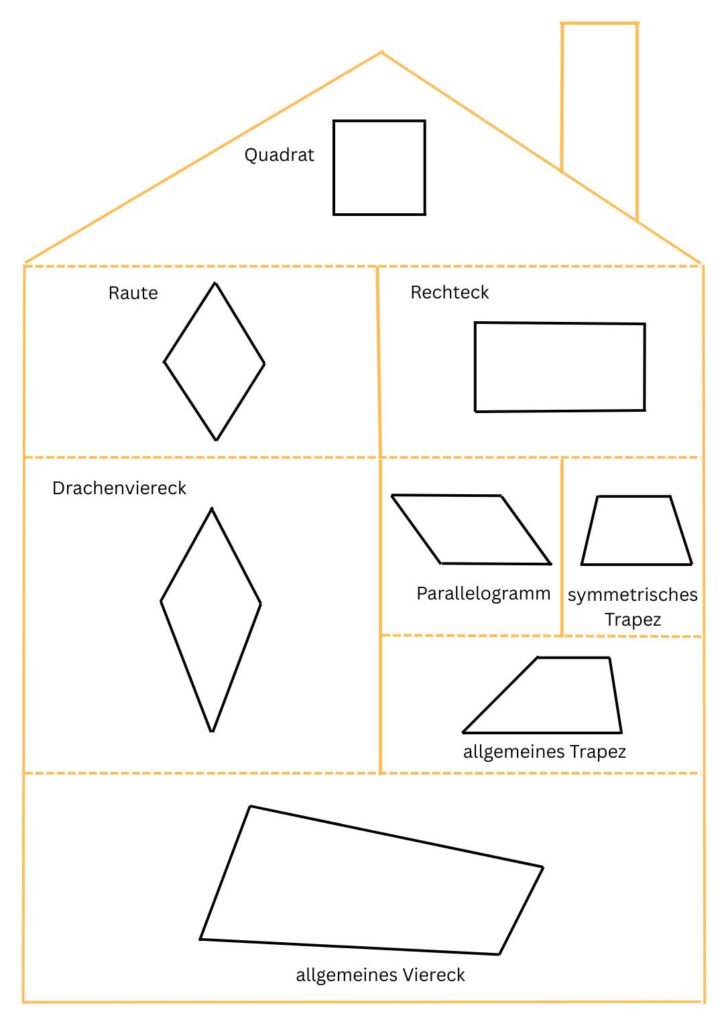
1. Allgemeines zum Haus der Vierecke
Im Haus der Vierecke befinden sich alle möglichen Vierecke – also alle Vierecksarten. Darüber hinaus wird im Haus der Vierecke ersichtlich, welche besonderen Eigenschaften diese haben und wie die Beziehungen zwischen diesen sind.
Hierbei weist ein Viereck immer eine größere Anzahl an Eigenschaften auf, je höhere es sich befindet. Ein Viereck hat also immer mehr Eigenschaften, wenn es quasi über einem anderen „wohnt“ bzw. das darunter „wohnende“ hat weniger Eigenschaften als das darüber.
Wenn ein Rechteck über einem anderen sich befindet – egal, in welcher Etage über ihm – dann weist dieses Viereck immer alle Eigenschaften der darunterliegenden Vierecke auf. Zudem hat es noch weitere Eigenschaften, weswegen es höher „wohnt“.
Von oben nach unten, vom Dachgeschoss über die verschiedenen Etagen bis zum Erdgeschoss, besteht also zwischen allen dort „wohnenden“ Vierecken eine Hierarchie hinsichtlich der Anzahl ihrer Eigenschaften. Hierbei gilt: Je höher ein Viereck „wohnt“ desto mehr Eigenschaft besitzt es, je tiefer es „wohnt“, desto weniger Eigenschaften hat es.
2. Die besonderen Eigenschaften der Vierecke
Vierecke unterscheiden sich gerade auch dadurch, dass sie besondere Eigenschaften aufweisen. Dadurch unterscheiden sie sich in der Form.
Die Eigenschaften, in denen sich Vierecke unterscheiden, sind: die Seiten, die Winkel, die Diagonalen und die Symmetrie.
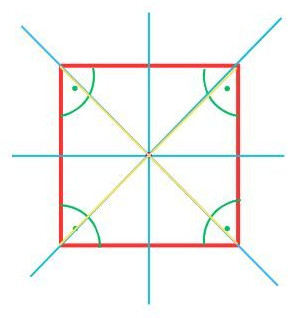
2.1 Quadrat
Es besitzt die meisten Eigenschaften und befindet sich daher ganz oben im Haus der Vierecke.
- Seiten: 4 gleich lange Seiten
- Winkel: 4 rechte Winkel (90 °)
- Diagonalen: gleich lang, schneiden sich senkrecht, halbieren einander
- Symmetrie: achsensymetrisch (horizontal, vertikal und diagonal), punktsymmetrisch und rotationssymmetrisch um 90°, und 270°
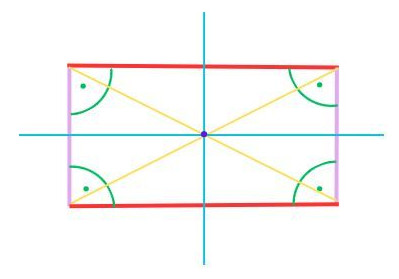
2.2 Rechteck
Das Rechteck befindet sich eine „Etage“ unter dem Quadrat.
- Seiten: gegenüberliegende Seiten gleich lang
- Winkel: 4 rechte Winkel (90 °)
- Diagonalen: schneiden sich senkrecht, halbieren einander
- Symmetrie: achsensymmetrisch (horizontal und vertikal), punktsymmetrisch
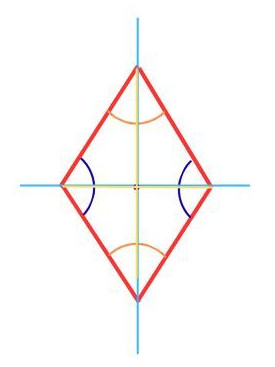
2.3 Raute (Rhombus)
Ebenfalls direkt eine „Etage“ unter dem Quadrat befindet sich die Raute bzw. der Rhombus.
- Seiten: 4 gleich lange Seiten
- Winkel: gegenüberliegende Winkel gleich groß
- Diagonalen: schneiden sich senkrecht, halbieren einander
- Symmetrie: achsensymmetrisch (diagonal), punktsymmetrisch
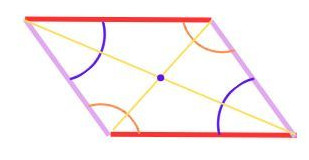
2.4 Parallelogramm
Zwei „Etagen“ unterhalb des Quadrates befindet sich das Parallelogramm.
- Seiten: gegenüberliegende Seiten gleich lang und parallel
- Winkel: gegenüberliegende Winkel gleich groß, benachbarte Winkel ergänzen sich zu 180°
- Diagonalen: halbieren einander
- Symmetrie: punktsymmetrisch
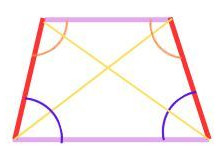
2.5 Symmetrisches Trapez
Ebenfalls zwei „Etagen“ unterhalb des Quadrates „wohnt“ das symmetrische Trapez.
- Seiten: ein Paar gegenüberliegender Seiten parallel, nicht-parallele Seiten gleich lang
- Winkel: benachbarte Winkel zur oberen und unteren Basis gleich groß
- Diagonalen: gleich lang
- Symmetrie: achsensymmetrisch (Mittelsenkrechte)
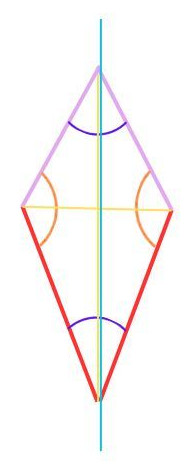
2.6 Drachenviereck
Ebenfalls zwei „Etagen“ unterhalb des Quadrates befindet sich auch das Drachenviereck.
- Seiten: zwei benachbarte Seiten gleich lang
- Winkel: gegenüberliegende gleich groß
- Diagonalen: schneiden sich senkrecht,
- Symmetrie: achsensymmetrisch (längere Diagonale)
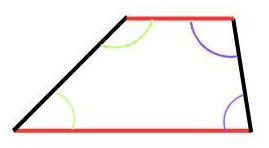
2.7 Allgemeines Trapez
Das allgemeine Trapez „wohnt“ mehrere Etagen unterhalb des Quadrates, da es nur noch wenige besondere Eigenschaften aufweist.
- Seiten: ein paar gegenüberliegende Seiten parallel
- Winkel: benachbarte Winkel zur oberen oder unteren Basis ergänzen sich zu 180°
- Diagonale: keine besonderen Eigenschaften
- Symmetrie: keine besonderen Eigenschaften
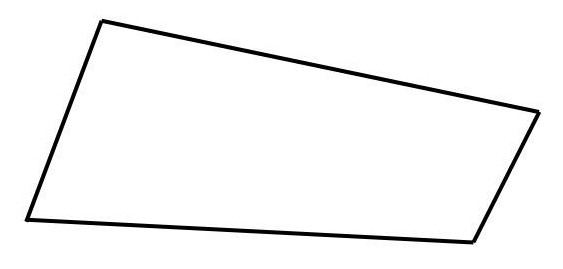
2.8 Allgemeines Viereck
Ganz unten, also im Erdgeschoss und damit am weitesten entfernt vom Quadrat, „wohnt“ das allgemeine Viereck.
- Seiten: keine besonderen Eigenschaften
- Winkel: keine besonderen Eigenschaften
- Diagonale: keine besonderen Eigenschaften
- Symmetrie: keine besonderen Eigenschaften
3. Die Beziehungen zwischen den Vierecken
Im Haus der Vierecke liegt eine sogenannte hierarchische Struktur vor. Von oben nach unten nehmen die besonderen Eigenschaften der Vierecke ab bzw. von unten nach oben nehmen diese zu.
Dadurch liegen verschiedene Beziehungen zwischen den Vierecken vor.
3.1 Die Teilmengenbeziehungen des Quadrats
Quadrat und Rechteck
Beziehung: Jedes Quadrat ist ein Rechteck.
Quadrat ⊂ Rechteck (Die Menge der Quadrate ist eine Teilmenge der Menge der Rechtecke)
Beziehung: Jedes Quadrat ist ein Rechteck.
Begründung: Ein Rechteck ist definiert als ein Viereck, bei dem alle vier Winkel 90° sind.

Quadrat und Raute (Rhombus)
Quadrat ⊂ Raute (Rhombus) (Die Menge der Quadrate ist eine Teilmenge der Menge der Rauten (Rhomben))
Beziehung: Jedes Quadrat ist eine Raute (Rhombus).
Begründung: Eine Raute (Rhombus) ist definiert als ein Viereck mit vier gleich langen Seiten.
Quadrat und Parallelogramm
Quadrat ⊂ Parallelogramm (Die Menge der Quadrate ist eine Teilmenge der Menge der Parallelogramme)
Beziehung: Jedes Quadrat ist ein Parallelogramm.
Begründung: Ein Parallelogramm ist definiert als ein Viereck mit Paaren parallel gegenüberliegender Seiten.
Quadrat und symmetrisches Trapez
Quadrat ⊂ symmetrisches Trapez (Die Menge der Quadrate ist eine Teilmenge der Menge der symmetrischen Trapeze)
Beziehung: Jedes Quadrat ist ein symmetrisches Trapez.
Begründung: Ein systemmetrisches Trapez ist definiert als ein Viereck mit einem Paar paralleler Seiten und einem Paar gleich langer Seiten.
Quadrat und Drachenviereck
Quadrat ⊂ Drachenviereck (Die Menge der Quadrate ist eine Teilmenge der Menge der Drachenvierecke)
Beziehung: Jedes Quadrat ist ein Drachenviereck.
Begründung: Ein Drachenviereck ist definiert als ein Viereck, bei dem zwei Paare benachbarter Seiten gleich lang sind.
Quadrat und allgemeines Trapez
Quadrat ⊂ allgemeines Trapez (Die Menge der Quadrate ist eine Teilmenge der Menge der allgemeinen Trapeze)
Beziehung: Jedes Quadrat ist ein allgemeines Trapez.
Begründung: Ein allgemeines Trapez ist definiert als ein Viereck mit mindestens einem Paar paralleler Seiten.
Quadrat und allgemeines Viereck
Quadrat ⊂ allgemeines Viereck (Die Menge der Quadrate ist eine Teilmenge der Menge der allgemeinen Vierecke)
Beziehung: Jedes Quadrat ist ein allgemeines Viereck.
Begründung: Ein allgemeines Viereck ist definiert als ein Viereck, das vier Seiten und vier Ecken haben muss.
3.2 Die Teilmengenbeziehungen des Rechtecks
Rechteck und Parallelogramm
Rechtecke ⊂ Parallelogramm (Die Menge der Rechtecke ist eine Teilmenge der Menge der Parallelogramme)
Beziehung: Jedes Rechteck ist ein Parallelogramm.
Begründung: Ein Parallelogramm ist definiert als ein Viereck mit Paaren parallel gegenüberliegender Seiten.
Rechteck und symmetrisches Trapez
Rechteck ⊂ symmetrisches Trapez (Die Menge der Rechtecke ist eine Teilmenge der Menge der symmetrischen Trapeze)
Beziehung: Jedes Rechteck ist ein symmetrisches Trapez.
Begründung: Ein systemmetrisches Trapez ist definiert als ein Viereck mit einem Paar paralleler Seiten und einem Paar gleich langer Seiten.
Rechteck und Drachenviereck
Rechteck ⊂ Drachenviereck (Die Menge der Rechtecke ist eine Teilmenge der Menge der Drachenvierecke)
Beziehung: Jedes Rechteck ist ein Drachenviereck.
Begründung: Ein Drachenviereck ist definiert als ein Viereck, bei dem zwei Paare benachbarter Seiten gleich lang sind.
Rechteck und allgemeines Trapez
Rechteck ⊂ allgemeines Trapez (Die Menge der Rechtecke ist eine Teilmenge der Menge der allgemeinen Trapeze)
Beziehung: Jedes Rechteck ist ein allgemeines Trapez.
Begründung: Ein allgemeines Trapez ist definiert als ein Viereck mit mindestens einem Paar paralleler Seiten.
Rechteck und allgemeines Viereck
Rechteck ⊂ allgemeines Viereck (Die Menge der Rechtecke ist eine Teilmenge der Menge der allgemeinen Vierecke)
Beziehung: Jedes Rechteck ist ein allgemeines Viereck.
Begründung: Ein allgemeines Viereck ist definiert als ein Viereck, das vier Seiten und vier Ecken haben muss.
3.3 Die Teilmengenbeziehungen der Raute (Rhombus)
Raute (Rhombus) und Parallelogramm
Raute (Rhombus) ⊂ Parallelogramm (Die Menge der Rauten (Rhomben) ist eine Teilmenge der Menge der Parallelogramme)
Beziehung: Jede Raute (Rhombus) ist ein Parallelogramm.
Begründung: Ein Parallelogramm ist definiert als ein Viereck mit Paaren parallel gegenüberliegender Seiten.
Raute (Rhombus) und symmetrisches Trapez
Raute (Rhombus) ⊂ symmetrisches Trapez (Die Menge der Rauten (Rhomben) ist eine Teilmenge der Menge der symmetrischen Trapeze)
Beziehung: Jede Raute (Rhombus) ist ein symmetrisches Trapez.
Begründung: Ein systemmetrisches Trapez ist definiert als ein Viereck mit einem Paar paralleler Seiten und einem Paar gleich langer Seiten.
Raute (Rhombus) und Drachenviereck
Raute (Rhombus) ⊂ Drachenviereck (Die Menge der Rauten (Rhomben) ist eine Teilmenge der Menge der Drachenvierecke)
Beziehung: Jede Raute (Rhombus) ist ein Drachenviereck.
Begründung: Ein Drachenviereck ist definiert als ein Viereck, bei dem zwei Paare benachbarter Seiten gleich lang sind.
Raute (Rhombus) und allgemeines Trapez
Raute (Rhombus) ⊂ allgemeines Trapez (Die Menge der Rauten (Rhomben) ist eine Teilmenge der Menge der allgemeinen Trapeze)
Beziehung: Jede Raute (Rhombus) ist ein allgemeines Trapez.
Begründung: Ein allgemeines Trapez ist definiert als ein Viereck mit mindestens einem Paar paralleler Seiten.
Raute (Rhombus) und allgemeines Viereck
Raute (Rhombus) ⊂ allgemeines Viereck (Die Menge der Rauten (Rhomben) ist eine Teilmenge der Menge der allgemeinen Vierecke)
Beziehung: Jede Raute (Rhombus) ist ein allgemeines Viereck.
Begründung: Ein allgemeines Viereck ist definiert als ein Viereck, das vier Seiten und vier Ecken haben muss.
3.4 Die Teilmengenbeziehungen des Parallelogramms
Parallelogramm und allgemeines Trapez
Parallelogramm ⊂ allgemeines Trapez (Die Menge der Parallelogramme ist eine Teilmenge der Menge der allgemeinen Trapeze)
Beziehung: Jedes Parallelogramm ist ein allgemeines Trapez.
Begründung: Ein allgemeines Trapez ist definiert als ein Viereck mit mindestens einem Paar paralleler Seiten.
Parallelogramm und allgemeines Viereck
Parallelogramm ⊂ allgemeines Viereck (Die Menge der Parallelogramme ist eine Teilmenge der Menge der allgemeinen Vierecke)
Beziehung: Jedes Parallelogramm ist ein allgemeines Viereck.
Begründung: Ein allgemeines Viereck ist definiert als ein Viereck, das vier Seiten und vier Ecken haben muss.
3.5 Die Teilmengenbeziehungen des symmetrischen Trapezes
Symmetrisches Trapez und allgemeines Trapez
Symmetrisches Trapez ⊂ allgemeines Trapez (Die Menge der symmetrischen Trapeze ist eine Teilmenge der Menge der allgemeinen Trapeze)
Beziehung: Jedes symmetrische Trapez ist ein allgemeines Trapez.
Begründung: Ein allgemeines Trapez ist definiert als ein Viereck mit mindestens einem Paar paralleler Seiten.
Symmetrisches Trapez und allgemeines Viereck
Symmetrisches Trapez ⊂ allgemeines Viereck (Die Menge der symmetrischen Trapeze ist eine Teilmenge der Menge der allgemeinen Vierecke)
Beziehung: Jedes symmetrische Trapez ist ein allgemeines Viereck.
Begründung: Ein allgemeines Viereck ist definiert als ein Viereck, das vier Seiten und vier Ecken haben muss.
3.6 Die Teilmengenbeziehungen des Drachenvierecks
Drachenviereck und allgemeines Viereck
Drachenviereck ⊂ allgemeines Viereck (Die Menge der Drachenvierecke ist eine Teilmenge der Menge der allgemeinen Vierecke)
Beziehung: Jedes Drachenviereck ist ein allgemeines Viereck.
Begründung: Ein allgemeines Viereck ist definiert als ein Viereck, das vier Seiten und vier Ecken haben muss.
3.7 Die Teilmengenbeziehungen des allgemeinen Trapezes
Allgemeines Trapez und allgemeines Viereck
Allgemeines Trapez ⊂ allgemeines Viereck (Die Menge der allgemeinen Trapeze ist eine Teilmenge der Menge der allgemeinen Vierecke)
Beziehung: Jedes allgemeine Trapez ist ein allgemeines Viereck.
Begründung: Ein allgemeines Viereck ist definiert als ein Viereck, das vier Seiten und vier Ecken haben muss.
3.8 Die Teilmengenbeziehungen des allgemeinen Vierecks
Es gibt keine Teilmengenbeziehungen zu anderen Vierecken.