1. Allgemeines zu Dreiecken
Dreiecke sind die einfachsten zweidimensionalen Figuren. Um eine Fläche zu erhalten, muss man mindestens drei Punkte miteinander verbinden. Dadurch erhält man ein Dreieck.
Neben besonderen Vierecken wie bspw. Rechtecken, Quadraten oder Trapezen sind im Fach Mathematik Dreiecke die zentralen geometrischen Figuren, die man entweder zeichnen oder anhand derer man Berechnungen vornehmen muss.
Die Winkelsumme eines Dreiecks beträgt 180°.
Definition eines Dreiecks:
Ein Dreieck stellt immer eine geometrische Figur dar. Es besteht aus drei Punkten, die man die Eckpunkte nennt und die mit Strecken miteinander verbunden sind.
2. Verschiedene Dreiecke
Aus der Möglichkeit, wie die drei Punkte bei einem Dreieck angeordnet sind, ergeben sich unterschiedliche Dreiecke.
2.1 Nach den Seiten
Je nachdem, welche Seitenlängen bei Dreiecken vorliegen, kann man diese unterschiedlich klassifizieren.
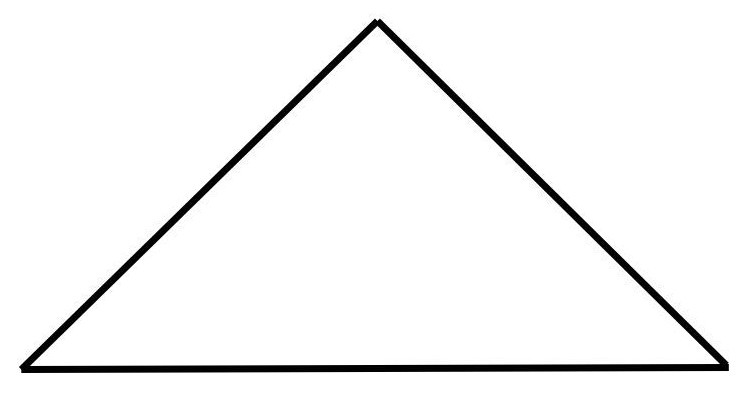
2.11 Ungleichseitiges Dreieck
Jede Seitenlänge des Dreiecks ist unterschiedlich lang.
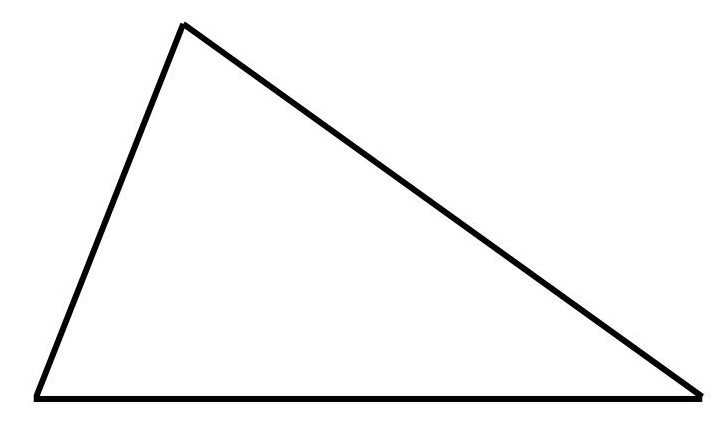
2.12 Gleichschenkliges Dreieck
Zwei Seitenlängen des Dreiecks sind gleich lang.
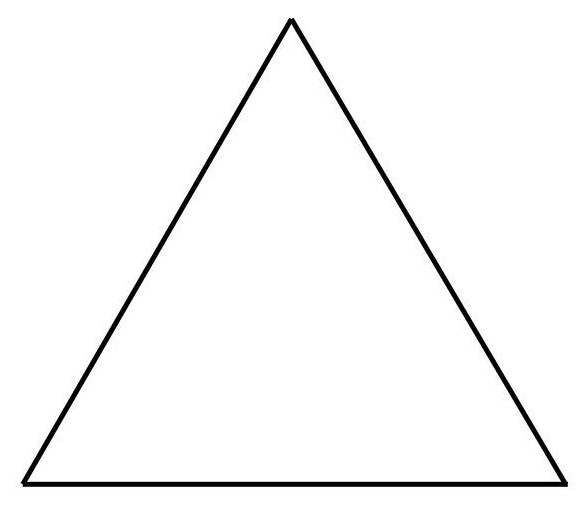
2.13 Gleichseitiges Dreieck
Alle Seitenlängen des Dreiecks sind gleich lang.
2.2 Nach den Winkel
Je nachdem, welche Winkel ein Dreieck aufweist, kann man Dreiecke ebenso klassifizieren.
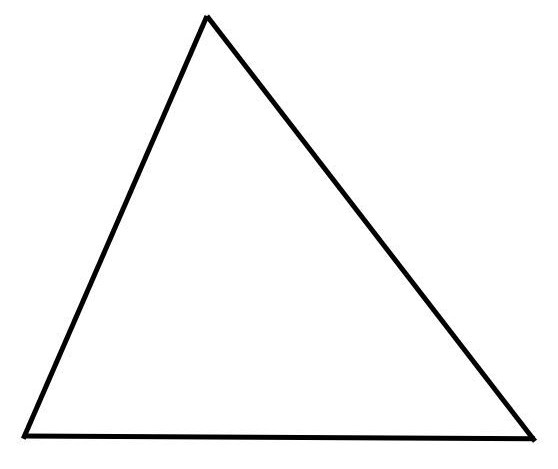
2.21 Spitzwinkliges Dreieck
In einem spitzwinkligen Dreieck sind alle Winkel kleiner als 90°.
2.22 Rechtwinkliges Dreieck
Bei einem rechtwinkligen Dreieck beträgt ein Winkel genau 90°. Der rechte Winkel wird mit einem Viertelkreisbogen mit Punkt in der Mitte markiert.
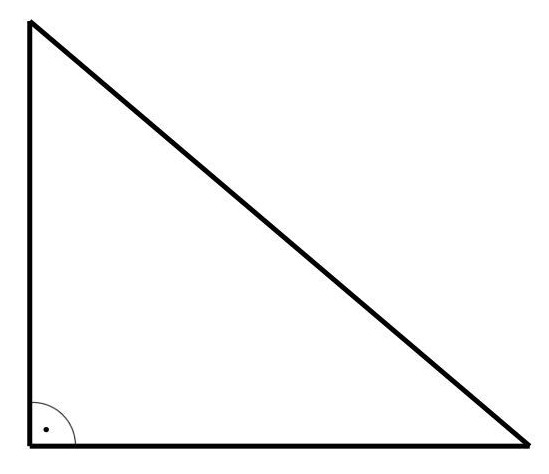
2.23 Stumpfwinkliges Dreieck
Ein stumpfwinkliges Dreieck liegt vor, wenn ein Winkel größer als 90° ist.
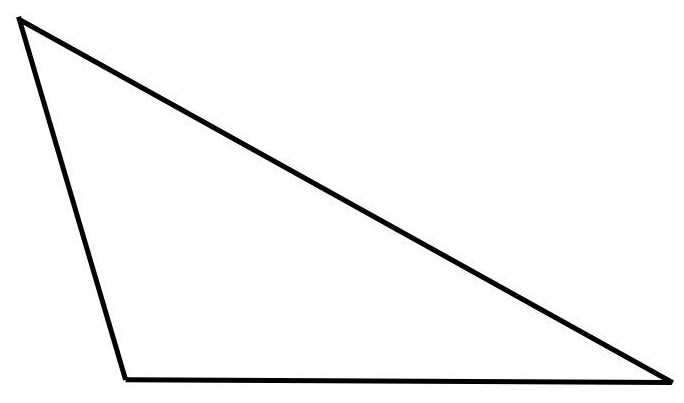
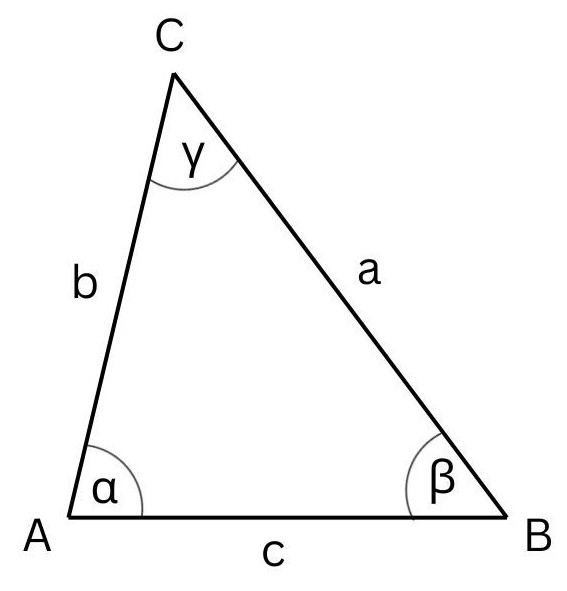
3. Die Beschriftung eines Dreiecks
Ein Dreieck weist folgende Beschriftung auf bzw. diese festgelegte Notation:
- Die drei Eckpunkte des Dreiecks weisen die Großbustaben A, B, C auf. Die Beschriftung A, B, C erfolgt gegen den Uhrzeigersinn!
- Die Seitenlängen weisen die Kleinbuchstaben a, b, c auf.
- Die Seitenlänge a liegt gegenüber dem Eckpunkt A, die Seitenläge b gegenüber dem Eckpunkt B und die Seitenlänge C gegenüber dem Eckpunkt C.
- Der Winkel beim Eckpunkt A wird mit α, der Winkel beim Eckpunkt B wird mit β und der Winkel beim Eckpunkt C mit γ bezeichnet.
Man spricht von dem Dreieck ABC, das die Seitenlängen a, b und c besitzt sowie die Winkel α, β und γ.