1. Die besondere Zahlenmenge der Primzahlen
Eine besondere Zahlenmenge innerhalb der Natürlichen Zahlen stellen die Primzahlen dar – und zwar aus zweierlei Gründen: Die Zahlenfolge der Primzahlen kann man bis heute durch keine einfache Formel wiedergeben; alle Zahlen, die keine Primzahlen sind, können in ein Produkt aus Primzahlen zerlegt werden (Primfaktorenzerlegung).
Definition Primzahlen:
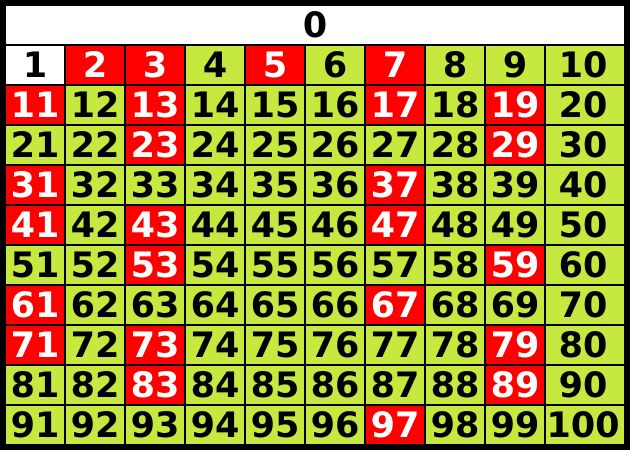
Alle Natürlichen Zahlen, die nur zwei Teiler vorweisen, nennt man Primzahlen. Hierbei ist eine Primzahl nur durch 1 und sich selbst teilbar. Die Zahl 1 ist keine Primzahl.
Bei den Zahlen 1 bis 20 ergeben sich daher als Primzahlen:
2, 3, 5, 7, 11, 13, 17, 19.
Die Zahlen 4, 6, 8, 10, 12, 14, 16, 18, 20 fallen weg, da diese gerade sind und somit auch durch 2 teilbar sind; die 15, da diese auch durch 3 und 5 teilbar ist.
Die kleinste Primzahl ist folglich die 2, auch die einzige, die Gerade ist.
2. Der Sieb des „Sieb des Eratosthenes“
Beim „Sieb des Eratosthenes“ handelt es sich um einen Algorithmus, also um eine eindeutige Handlungsvorschrift bzw. Verfahren, womit man innerhalb einer Zahlenmange der natürlichen Zahlen mit einem Maximalwert alle darin vorkommenden Primzahlen bestimmen kann. Dieser Algorithmus ist nach dem griechischen Mathematiker Eratosthenses benannt, der im 3. Jahrundert vor Christus lebte. Er gilt aber nicht als der Erfinder dieses Verfahrens, da dieses schon sehr viel früher bekannt war, sondern nur als der Namensgeber für das Verfahren als „Sieb“.
2.1 Anwendung des „Sieb des Eratosthenes“
Zuerst schreibt man alle natürlichen Zahlen, beginnend ab der Zahl 2 (da die Zahl 1 nicht zu den Primzahlen gezählt wird), der Reihe nach auf. Das macht man bis zu einem selbst gewählten Maximalwert S. Zum Beispiel schreibt man alle natürlichen Zahlen, von der 2 anfangend, bis zur Zahl 200 auf – wie es hier der Fall ist. Der Übsichtlichkeit wegen wurden hier die Zahlen 2 bis 200 der Reihe nach in einer Tabelle aufgeschrieben und jeweils pro Zeile der Zahlenwert bis zu einem Vielfachen von 10. Alle innerhalb dieser Tabelle unmarkierten Zahlen stellen nun potentielle Primzahlen dar, die nun peu à peu, Schritt für Schritt, weniger werden bzw. „ausgesiebt“ werden. Das geschieht nun folgendermaßen: Die kleinste unmarkiete Zahl ist immer eine Primzahl. Hier ist es die Zahl 2. Von dieser Zahl ausgehend werden nun alle weiteren Vielfachen von 2 markiert, da diese ja keine Primzahlen mehr sein können. Hier werden die Vielfachen von 2 mit der Farbe Rot hervorgehoben. Die nächsthöhere unmarkierte Zahl stellt wiederum eine Primzahl dar. Dieses ist hier die 3. Alle Vielfachen von 3 werden nun markiert. Hier mit der Farbe Grün. Bereits markierte Zahlen werden hierbei nicht berücksichtig, da diese ja keine Primzahlen mehr sein können. Die nächsthöhere ist nun die 5. Dies Vielfachen von der Zahl 5 werden hier nun mit der Farbe Blau markiert. Die nächsthöhere Primzahl ist nun die 7. Die Vielfachen von dieser Zahl werden nun mit der Farbe Gelb markiert. Die nächsthöhere Primzahl ist nun die 11, alle Vielfachen hiervon werden mit der Farbe Organge hervorgehoben. Die nächsthöre ist nun die Primzahl 13. Hiervon gibt es nun nur noch ein Vielfaches innerhalb der Zahlen bis 200, und zwar die Zahl 169. Diese wird hier mit der Farbe Braun markiert. Nun gibt es keine weiteren Vielfachen mehr und somit hat man alle Primzahlen „ausgesiebt.“
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 |
| 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 |
| 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 |
| 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 |
| 71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 | 80 |
| 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 |
| 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 | 100 |
| 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 | 110 |
| 111 | 112 | 113 | 114 | 115 | 116 | 117 | 118 | 119 | 120 |
| 121 | 122 | 123 | 124 | 125 | 126 | 127 | 128 | 129 | 130 |
| 131 | 132 | 133 | 134 | 135 | 136 | 137 | 138 | 139 | 140 |
| 141 | 142 | 143 | 144 | 145 | 146 | 147 | 148 | 149 | 150 |
| 151 | 152 | 153 | 154 | 155 | 156 | 157 | 158 | 159 | 160 |
| 161 | 162 | 163 | 164 | 165 | 166 | 167 | 168 | 169 | 170 |
| 171 | 172 | 173 | 174 | 175 | 176 | 177 | 178 | 179 | 180 |
| 181 | 182 | 183 | 184 | 185 | 186 | 187 | 188 | 189 | 190 |
| 191 | 192 | 193 | 194 | 195 | 196 | 197 | 198 | 199 | 200 |
Die Primzahlen von 2 bis 200 sind nun alle diese, von denen es kein Vielfaches einer Primzahl gibt, bzw. diejenigen, die nicht markiert wurden. Die Primzahlen, hier mit der Farbe Schwarz, sind also: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199
Dieses Verfahren, den „Sieb des Eratosthenes“, kann man nun auch auf einem beliebigen Maximalwert S hin erweitern. Je mehr Zahlen darin enthalten sind, desto schwieriger gestaltet sich die Bestimmung der Primzahlen bzw. umso mühsamer das „Aussieben“.
3. Die Primfaktorzerlegung bei Nicht-Primzahlen
Jede natürliche Zahl, die keine Primzahl ist, kann in ein Produkt aus Primzahlen zerlegt werden.
4 = 2 · 2
6 = 2 · 3
8 = 2 · 2 · 2
10 = 2 · 5
12 = 2 · 2 · 3
14= 2 · 7
15 = 3 · 5
16 = 2 · 2 · 2 · 2
18 = 2 · 3 · 3
20 = 2 · 2 · 5
Beispiel: Zerlegung der Zahl 300 in ein Produkt aus Primzahlen:
300 in Primfaktoren: 300 : 10 = 30; 30 : 10 = 3;10 = 5 = 2; 10 : 5 = 2
Wenn man 300 mit dem Teiler 10 teilt, dann erhält man 30. Den Teiler 10 kann man mit dem Teiler 5 teilen und erhält eine 2. Die 30 kann man wieder mit 10 teilen und erhält 3. Die 10 teilt man noch einmal mit 5 und erhält wiederum 2. Jetzt hat man die Zahl 300 in Primzahlen zerlegt. Die Zahl weist zweimal eine 2, eine 3 und zweimal eine 5 als Teiler in Form von Primzahlen auf.
Die Primfaktorzerlegung sieht nun folgendermaßen aus:
300 = 5 · 2 · 5 · 3 · 2 = 2 · 2 · 3 · 5 · 5 = 22 · 3 · 52
300 in Primfaktoren: 300 : 3 = 100; 100 : 10 = 10; 10 : 5 = 2; 10 : 5 = 2
Wenn man 300 mit dem Teiler 3 teilt, erhält man 100. 100 kann man mit 10 teilen und erhält 10. 10 geteilt durch 5 ergibt 2. Das gilt natürlich auch bei der zweiten Zehn: 10 geteilt 5 ist gleich 2.
Es ergibt sich diese Primfaktorzerlegung.
300
= 3 · 5 · 2 · 5 · 2 = 2 · 2 · 3 · 5 · 5 (als Produkt)
= 22 · 3 · 52 (als Produkt in der Potenzschreibweise)
300 in Primfaktoren: 300 : 2 = 150; 150: 10 = 15; 10 : 2 = 5; 15 : 5 = 3
Wenn man 300 mit 2 teilt, erhält man 150. 150 geteilt durch 10 ist 15. 10 durch 2 = 5. Und 15 geteilt durch 5 ergibt 3.
Die Primfaktorzerlegung ist hier Folgende:
300 = 2 · 2 · 5 · 5 · 3 = 2 · 2 · 3 · 5 · 5 = 22 · 3 · 52
Wie man sieht, ergeben sich – egal, in welche Teiler man die 300 zerlegt – immer die gleichen und die gleiche Anzahl von Primzahlen und somit immer die gleiche Primfaktorzerlegung.
Bei der Teilbarkeit von Zahlen kann man die Primfaktorzerlegung heranziehen, um mittels Primfaktoren zu ermitteln, was deren größter gemeinser Teiler (ggT) ist oder das kleinste gemeinsame Viefache (kgV).
3.1 Bestimmung des größten gemeinsamen Teilers (ggT)
Es sind die Zahlen 24, 36, 60 gegeben. Man möchte nun herausfinden, welchen größten gemeinsamen Teiler (ggT) diese Zahlen haben. Auf den ersten Blick sieht man sofort, dass alle drei Zahlen gerade sind, also durch 2 teilbar sein müssen. Ist das aber wirklich schon der größte gemeinsame Teiler? Sicherlich nicht. Man kann auch mit einem geübteren Blick sofort erkennen, dass alle Zahlen auch durch 4 teilbar sind (wenn man die 4er Malreihe beherrscht und erkennt, dass 40 + 20 = 60 ist). Ist das aber bereits der größte gemeinsam Teiler? Genau kann man das nicht so einfach sagen. Die Primfaktorzerlegung gibt hierüber aber eine Eindeutigkeit.
24 = 2 · 2 · 2 · 3 = 23 · 3, gleiche Primfaktoren: 2 · 2 · 3 = 22 ·3
36 = 2 · 2 · 3 · 3 = 22 · 32, gleiche Primfaktoren: 2 · 2 · 3 = 22 ·3
60 = 2 · 2 · 3 · 5 = 22 · 3 · 5, gleiche Primfaktoren: 2 · 2 · 3 = 22 · 3
Die gemeinsamen Primfaktoren bei den Zahlen 24, 36, und 60 sind also 22 · 3, da diese bei der Primfaktorzerlegung aller Zahlen enthalten sind. Demzufolge ist der größte gemeisame Teiler (ggT): 12 ( 22 · 3 = 12).
Ermitteln des größten gemeinsamen Teilers (ggT):
Um den größten gemeinsamen Teiler (ggT) bei unterschiedlichen Zahlen zu bestimmen, ermittelt man bei deren Primfaktorzelegung die niedrigsten Potenzen ihrer gemeinsamen Primfaktoren.
Aufgabe:
Bestimme den größten gemeinsamen Teiler bei den Zahlen 60, 90, 150.
Mittels Primfaktorzerlegung ergibt sich Folgendes:
60 = 2 · 2 · 3 · 5 = 22 · 3 · 5, gleiche Primfaktoren: 2 · 3 · 5
90 = 2 · 3 · 3 · 5 = 2 · 32 · 5, gleiche Primfaktoren: 2 · 3 · 5
150: 2 · 3 · 5 · 5 = 2 · 3 · 52, gleiche Primfaktoren: 2 · 3 · 5
Der größte gemeinsam Teiler (ggT) = 30 (2 · 3 · 5 = 30)
3.2 Bestimmung des kleinsten gemeinsamen Vielfaches (kgV)
Es sind die Zahlen 12, 18, 30 gegeben. Man möchte nun ermitteln, welchen kleinste gemeinsame Vielfache (kgV) diese Zahlen haben.
12 = 2 · 2 · 3 = 22 · 3, höchste Potenz: 22
18 = 2 · 3 · 3 = 2 · 32, hochste Potenz: 32
30 = 2 · 3 · 5 = 2 · 3 · 5, höchste Potenz: 5
Das kleinste gemeinsaem Vielfaches (kgV) der Zahlen 12, 18, 30 ist 22 · 32 · 5 = 180.
Ermitteln des kleinsten gemeinsamen Vielfaches (kgV):
Um das größte gemeinsame Vielfache (kgV) bei unterschiedlichen Zahlen zu bestimmen, ermittelt man bei deren Primfaktorenzerlegung die höchsten Potenzen ihrer auftretenden Primfaktoren.
Aufgabe:
Bestimme das kleinste gemeinsame Vielfache (kgv) bei den Zahlen 8, 14 und 20.
Mittels Primfaktorzerlegung ergibt sich Folgendes:
8 = 2 · 2 · 2 = 23, höchste Potenz: 23
14 = 2 · 7, höchste Potenz: 7
20 = 2 · 2 · 5 =22 · 5, höchste Potenz: 5
Das kleinste gemeinsaem Vielfache (kgV) beträgt: 23 · 5 · 7 = 280.