1. Allgemeines zur Wurzelfunktion
Die Potenzfunktion hat die Zuordnungsvorschrift f: x ↦ a · xn und die Funktionsgleichung f(x) = a · xn (n ∈ N). Der Definitionsbereich beinhaltet ℝ\{0}.
Durch Spiegelung der Funktion an der 1. Winkelhalbierenden kann man die Funktion zur sogenannten Wurzelfunktion umkehren.
Man erhält dann diese Zuordnungsvorschrift: f−1: x ↦ $\sqrt[n]{\frac{\mathrm{x}}{\mathrm{a}}}$
Die neue Funktion hat dann folgende Funktionsgleichung:
f(x) = $\sqrt[n]{\frac{\mathrm{x}}{\mathrm{a}}}$
mit x ≥ 0 (n ∈ N, a ≠ 0).
Der Definitonsbereich beinhaltet ℝ\{0}, wobei gilt x/a ≥ 0.
2. Die Wurzelfunktion durch Umkehrung aus der Potenzfunktion
Man erhält die Wurzelfunktion durch Umkehrung der Potenzfunktion, und zwar folgendermaßen:
Zuerst kehrt man den x- und y-Wert um. Die Gleichung sieht dann so aus:
x = a · yn
Diese Gleichung löst man nach y auf.
x = a · yn | : a
$\frac{\mathrm{x}}{\mathrm{a}}$ = yn | $\sqrt[\mathrm{n}]{}$
$\sqrt[n]{\frac{\mathrm{x}}{\mathrm{a}}}$ = y
y = $\sqrt[n]{\frac{\mathrm{x}}{\mathrm{a}}}$
Die Umkehrung der Zuordnungsvorschrift ist diese:
f: x ↦ a · xn entspricht: f−1 = $\sqrt[n]{\frac{\mathrm{x}}{\mathrm{a}}}$
Die Umkehrung der Funktionsgleichung ist folgende:
f(x) = a · xn entspricht: f−1(x) = $\sqrt[n]{\frac{\mathrm{x}}{\mathrm{a}}}$
3. Verschiedene Wurzelfunktionen
f(x) = a · $\sqrt[\mathrm{n}]{\mathrm{x}}$
So lautet die allgemeine Wurzelfunktion.
n bestimmt den Wurzelgrad und beeinflusst, wie stark die Funktion steigt oder fällt.
Der Koeffizient a beeinflusst hierbei, ob die Funktion eher gestaucht oder gestreckt ist.
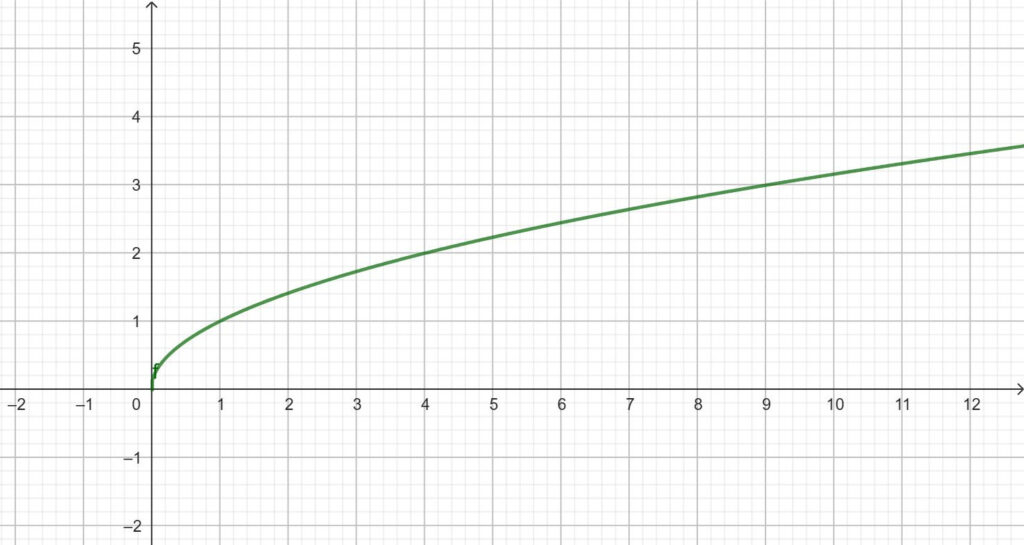
3.1 Der Graph der Quadratwurzelfunktion
Die Quadratwurzelfunktion hat folgende Funktionsgleichung:
f(x) = $\sqrt{\mathrm{x}}$
Der Graph dieser Funktion verläuft folgendermaßen: